poj 3347 Kadj Squares（计算几何）

题目链接：点击打开链接

Kadj Squares

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 2928		Accepted: 1146

Description

In this problem, you are given a sequence S₁, S₂, ..., S_n of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let b_i be the x coordinates of the bottom vertex of S_i. First, put S₁ such that its left vertex lies on x=0. Then, put S₁, (i > 1) at minimum b_i such that

• b_i > b_i-1 and
• the interior of S_i does not have intersection with the interior of S₁...S_i-1.

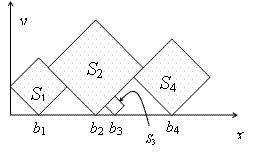
The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S₁, S₂, and S₄ have this property. More formally, S_i is visible from above if it contains a point p, such that no square other than S_i intersect the vertical half-line drawn from p upwards.

Input

The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of S_i. The input is terminated by a line containing a zero number.

Output

For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.

Sample Input

4
3 5 1 4
3
2 1 2
0

Sample Output

1 2 4
1 3

题意：依次给出n个正方形的边长，问从上往下看能看到哪几个正方形，从小到大输出。

思路：先用计算几何知识求出每个正方形的的左右端点坐标，然后枚举正方形，再判断其与前面的多边形的关系，如果有覆盖的情况产生，则更新。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 55
#define eps 1e-10
#define sqrt2 1.414214
struct point
{
    double l,r,len;
} p[N];
double maxn(double a,double b)
{
    if(a-b>eps) return a;
    return b;
}
int main()
{
    int n;
    while(~scanf("%d",&n)&&n)
    {
        for(int i=0; i<n; i++)
        {
            scanf("%lf",&p[i].len);
            p[i].l=0;
            double l;
            for(int j=0; j<i; j++)
            {
                if(p[j].len-p[i].len>eps)
                    l=p[j].l+(sqrt2/2)*(p[j].len+p[i].len);
                else
                    l=p[j].l+(sqrt2/2)*(3*p[j].len-p[i].len);
                p[i].l=maxn(p[i].l,l);
            }
            p[i].r=p[i].l+sqrt2*p[i].len;
        }
        for(int i=1; i<n; i++)
        {
            for(int j=0; j<i; j++)
            {
                if(p[i].len>p[j].len&&p[j].r-p[i].l>eps)
                    p[j].r=p[i].l;
                if(p[i].len<p[j].len&&p[j].r-p[i].l>eps)
                    p[i].l=p[j].r;
            }
        }
        for(int i=0; i<n; i++)
        {
            if(p[i].r>p[i].l)
                printf("%d ",i+1);
        }
        printf("\n");
    }
    return 0;
}