题目链接:http://codeforces.com/problemset/problem/369/E
题意:
在一维的x轴上
给定n个线段, m个询问
每个询问 cut个点, 问该点集覆盖的线段数量
思路:
ans[i] 表示 第 i 个询问的答案,设 ans[i] = n, 再减去 不在点集中的线段
对于第i个询问,预处理出不在 {点集内的线段} ,
如第2个询问的点集是{4,5},
则预处理出线段{ [1,3], [6,inf] }
则对于第2个答案 ans = n - |{所有包含于 { [1,3], [6,inf] }这个线段点集}|
树状数组中存的是输入的线段。
sum(x) = 求和[1,x];
add(x) = [x,inf]++;
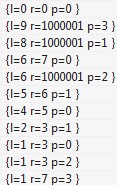
附:预处理排序后的结果图,p为0表示输入的线段,p>0表示第p个询问处理出的线段
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <string.h>
using namespace std;
#define N 1000005
#define inf N-1
int c[N], maxn;
inline int lowbit(int x){return x&(-x);}
void add(int pos, int val){while(pos<=maxn)c[pos]+=val,pos+=lowbit(pos);}
int sum(int pos){int ans = 0;while(pos)ans+=c[pos],pos-=lowbit(pos);return ans;}
struct node{
int l,r,id;
bool operator<(const node&a)const{
return a.l<l||a.l==l&&a.r>r||a.l==l&&a.r==r&&a.id>id;
}
node(int a=0,int b=0,int c=0):l(a),r(b),id(c){}
}a[N];
int ans[N];//处理出不在{点集内的线段},则ans = n - 输入中所有包含于{点集内的线段}
int main(){
int n,m,i,j;
maxn = inf;
while(~scanf("%d%d",&n,&m)){
for(i=1;i<=n;i++)scanf("%d %d",&a[i].l,&a[i].r),a[i].id = 0;
int top = n, x;
for(i=1;i<=m;i++)
{
scanf("%d %d",&j,&x);
if(x>1)a[++top] = node(1,x-1,i);
while(--j){
int now; scanf("%d",&now);
if(x+1<=now-1)a[++top] = node(x+1,now-1,i);
x = now;
}
if(x+1<=maxn-1)a[++top] = node(x+1,maxn-1,i);
}
for(i=1;i<=m;i++)ans[i] = n;
memset(c, 0, sizeof c);
sort(a+1,a+top+1);
for(i=1;i<=top;i++)
if(a[i].id)ans[a[i].id] -= sum(a[i].r);
else add(a[i].r,1);
for(i=1;i<=m;i++)printf("%d\n",ans[i]);
}
return 0;
}
























 755
755

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








