棋盘染色问题

背景

题目网址有两个，对，双倍经验，只是差距甚远。

紫题：https://www.luogu.com.cn/problem/P1817​​​​​​

绿题：https://www.luogu.com.cn/problem/P1790（注意我这个代码输出时要除以2）

题目描述

给定一个 N*M的网格，每个格子可以染成黑色或者白色，要求所有黑色格子连通，所有白色格子连通，并且至少有一个黑色格子贴边，至少有一个白色格子贴边。问有多少种染色方法？

输入格式

第一行有两个正整数 N，M。

输出格式

只有一个正整数表示答案。

样例

输入
1 2

输出 
2

输入
2 3

输出 
30

提示

对于 100 的数据：1 ≤N ≤ 7，1≤M≤8。

分析

第一反应——深搜（代码如下），但是——

int _x[ ] = {0, -1, 1, 0, 0}, _y[ ] = {0, 0, 0, -1, 1},/*枚举x,y的可能值*/ n, m/*输入的长、宽*/, sum/*总数*/;// count[10][10];
const int M = 20;//图的大小
bool mp[M][M];//一个图
inline void dfs(int x, int y) {//爆搜代码
	if (x < 1 || y < 1 || x >= n || y >= m)++sum;//统计个数
	else {
		mp[x][y] = true;
		for (register int i = 4; i > 0; --i) {
			int xx = x + _x[i], yy = y + _y[i];
			if (mp[xx][yy] == false)dfs(xx, yy);
		}
		mp[x][y] = false;
	}
}

超时3个点（肯定的）。。。。。。

那么怎么办？一看数据范围，眼睛一亮——

打表（可能不讲武德了）

随后我顺手打了一个代码，直接把代码都打好了（不得不说我太懒了），如下——

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")//不得不开个挂来加速度
#include <bits/stdc++.h>
#define int long long//也是习惯了
using namespace std;
int _x[ ] = {0, -1, 1, 0, 0}, _y[ ] = {0, 0, 0, -1, 1},/*枚举x,y的可能值*/ n, m/*输入的长、宽*/, sum/*总数*/;// count[10][10];
const int M = 20;//图的大小
bool mp[M][M];//一个图
inline void dfs(int x, int y) {//爆搜代码
	if (x < 1 || y < 1 || x >= n || y >= m)++sum;//统计个数
	else {
		mp[x][y] = true;
		for (register int i = 4; i > 0; --i) {
			int xx = x + _x[i], yy = y + _y[i];
			if (mp[xx][yy] == false)dfs(xx, yy);
		}
		mp[x][y] = false;
	}
}
int a[2][2] {
	{1, 1}, {1, 1},
};//大致输出的样子
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	printf("#include <bits/stdc++.h>\n#define int long long\nusing namespace std;\nsigned main(){\n");
	printf("	register int answer[7][8]={\n");//模拟打这个数组的样子
	for (n = 1; n <= 7; ++n) {//枚举n
		printf("	{");
		for (m = 1; m <= 8; ++m) {//枚举m
			sum=0;
			for (register int i = 1; i < n; ++i) {
				memset(mp, false, sizeof(mp));
				mp[i][0] = true;
				dfs(i, 1);
			}
			for (register int i = 1; i < m; ++i) {
				memset(mp, false, sizeof(mp));
				mp[0][i] = true;
				dfs(1, i);
			}
			printf("%lld,",sum*2);//细节：由于黑白可互换，所以乘上2
		}
		printf("},\n");
	}
	printf("	};\n	register int n,m;\n	cin>>n>>m;\n	cout<<answer[n-1][m-1]<<endl;\n	return 0;\n}");//大致就这样了
	return 0;
}

运行出来这个效果——

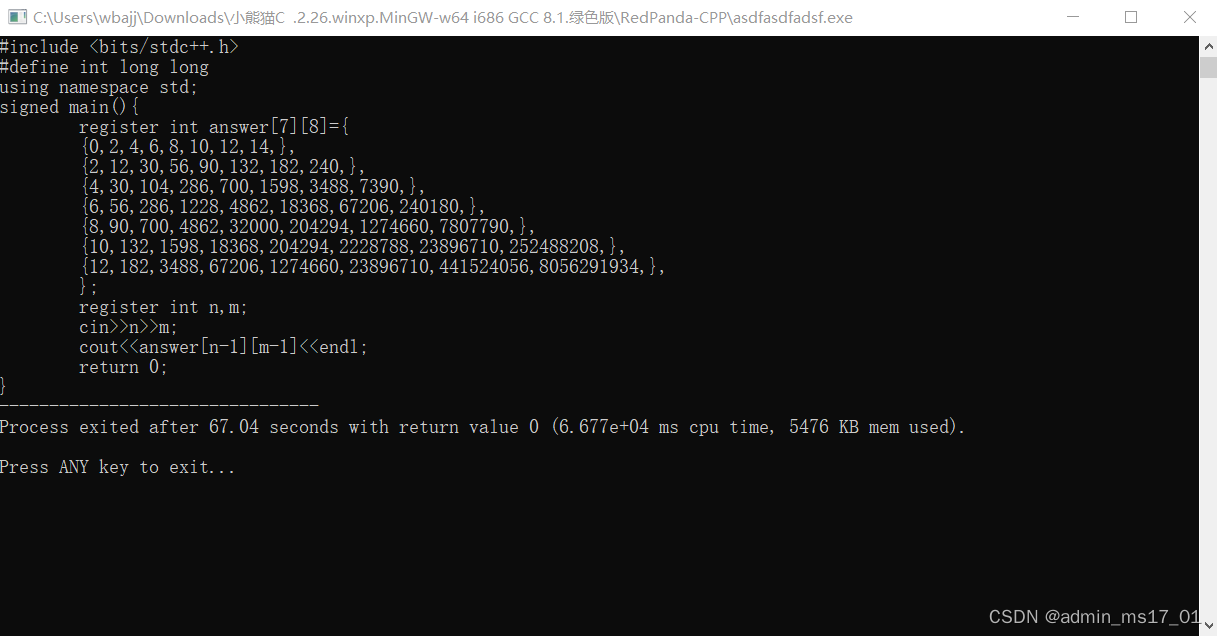
直接复制粘贴就是了。

最后

我这个方法有些投机取巧，若数据范围庞大就要上正解插头dp了，而我又不会，只好这样了

同时，我感觉这是洛谷上最水的紫题，建议降绿

还有我一直没时间发博文，今天也是赶出来的，所以请大家原谅。