最短路径算法：Bellman-ford算法，Dijkstra算法，floyd-warshall算法，johnson算法（数据结构算法导论期末复习）

​

单源最短路径

Bellman-ford算法

边的权重可以为负值，可以检测负权环

为什么可以检测负权环？

gpt：

Bellman-Ford算法之所以能够检测负权环，是因为它对图进行了多次松弛操作。松弛操作的本质是尝试通过更新边的权重来改善两个节点之间的最短路径估计。在Bellman-Ford算法中，每轮松弛都会逐渐改进最短路径估计。

如果图中包含负权环，那么从负权环中的某个节点出发，可以无限次地绕环一周，从而导致路径的权重变得更小。Bellman-Ford算法的每一轮都会尝试对所有边进行松弛，如果存在从源节点可达的权重更小的路径，那么算法就会更新这个路径。如果存在负权环，由于可以无限次地绕环，权重可以无限减小，Bellman-Ford算法将检测到这种情况。

具体来说，Bellman-Ford算法的伪代码如下：

1. 初始化：设置源节点的最短路径估计为0，其他节点的最短路径估计为正无穷。
2. 进行V-1轮松弛操作，其中V是图中的节点数。
3. 进行第V轮松弛操作，如果在这一轮中发现了更短的路径，则说明图中存在负权环。

如果在第V轮中依然可以松弛边，那么说明至少存在一个节点可达的路径上包含了一个负权环。

Bellman-Ford算法的时间复杂度是O(V * E)

正确性：

引理24.2 设𝐺 = （𝑉，𝐸） 为一个带权重的源结点为𝑠的有向图，其权重函数为 𝜔: 𝐸 → 𝑅。假定图𝐺不包含从源结点𝑠可以到达的权重为负值的环路。那么在算法 BELLMAN-FORD的第2~4行的for循环执行了 𝑉 − 1次之后，对于所有从源结点𝑠可 以到达的结点𝑣，我们有𝑣. 𝑑 = 𝛿 （𝑠, 𝑣） 。

证明：考虑任意从𝑠可以到达的结点𝑣，设𝑝 =< 𝑣0, 𝑣1, … , 𝑣𝑘 >为从𝑠到𝑣之间的任 意一条最短路径，这里𝑣0 = 𝑠, 𝑣𝑘 = 𝑣。因为最短路径是简单路径，𝑝最多包含 |𝑉| − 1条边，𝑘 ≤ |𝑉|− 1。算法第2~4行的for循环每次松弛所有的 𝐸 条边。在 第𝑖次松弛操作时，这里𝑖 = 1,2, … , 𝑘，被松弛的边中包含边 （𝑣_𝑖−1, 𝑣_𝑖 ）。根据路径松弛性质，𝑣. 𝑑 = 𝑣_𝑘. 𝑑 = δ （𝑠, 𝑣_𝑘） = δ (𝑠, 𝑣) 。

路径松弛性质(引理24.15) 若𝑝 =< 𝑣0, 𝑣1, … , 𝑣𝑘 >是从源点𝑠 = 𝑣0到点𝑣𝑘的一条 最短路径，且对𝑝中的边进行松弛的次序为 𝑣0, 𝑣1 , 𝑣1, 𝑣2 , … , 𝑣𝑘−1, 𝑣𝑘 ，则 𝑣_𝑘. 𝑑 = δ (𝑠, 𝑣_𝑘) 。该性质的成立与任何其他的松弛操作无关，即使这些松弛操作 是与对𝑝上的边进行的松驰操作穿插进行的。

推论24.3 设𝐺 = 𝑉，𝐸 是一带权重的源结点为𝑠的有向图，其权重函数为𝜔: 𝐸 → 𝑅。假定图𝐺不包含从源结点s可以到达的权重为负值的环路，则对于所有结点 𝑣 ∈ 𝑉，存在一条从源结点𝑠到结点𝑣的路径，当且仅当BELLMAN-FORD算法终止时 有𝑣. 𝑑 < ∞。

定理24.4（Bellman-Ford算法的正确性) 设BELLMAN-FORD算法运行在一带权重的 源结点为𝑠的有向图𝐺 = (𝑉，𝐸) 上，该图的权重函数为𝜔: 𝐸 → 𝑅。如果图𝐺不包含从源结点𝑠可以到达的权重为负值的环路，则算法将返回TRUE值，且对于所有结点𝑣 ∈ 𝑉，前驱子图𝐺_𝜋是一棵根结点为𝑠的最短路径树。如果图𝐺包含一条从源结点𝑠可以到达的权重为负值的环路，则算法将返回FALSE值。

证明:

假定𝐺不包含从𝑠可以到达的权重为负值的环路。

​ 首先证明，对于所有结点 𝑣 ∈ 𝑉，在算法BELLMAN-FORD终止时，有𝑣. 𝑑 = δ (𝑠, 𝑣) 。如果结点𝑣是从𝑠可以到达的，则引理24.2证明了本论断。如果结点𝑣不能从𝑠到达，则该论断可以从非路径性质获得(均为正无穷)。因此，该论断得到证明。

​ 综合前驱子图性质和本论断可以推导出𝐺_𝜋是 一棵最短路径树。 现在，使用上述论断来证明BELLMAN-FORD算法返回的是TRUE值。在算法BELLMANFORD终止时，对于所有的边 𝑢, 𝑣 ∈ 𝐸，有 𝑣. 𝑑 = δ （𝑠, 𝑣） ≤ δ （𝑠, 𝑢） + ω （𝑢, 𝑣） = 𝑢. 𝑑 + ω （𝑢, 𝑣） 因此，如果算法第6行中没有任何测试可以让BELLMAN-FORD算法返回FALSE值。因此， 它一定返回的是TRUE值。

Dijkstra算法

算法要求所有边的权重为非负值。 因为Dijkstra算法的关键假设是，一旦某个节点的最短路径被确定，就不再更新该节点的最短路径。负权边会破坏这个假设。在存在负权边的情况下，通过一个节点可能会使得到达其他节点的路径更短，从而违反了Dijkstra算法的基本假设。

即是贪心算法，也是动态规划算法。

• 每次做出最贪心的选择（距离增加值最小,选出到源点距离最小的点）。
• 先求小问题（短的最短距离），再利用最优子结构特性求大问题（长的最短 距离）。

Dijkstra算法的总运行时间依赖于最小优先队列的实现。

• 二叉堆 O(𝑬 𝒍𝒈𝑽) 。每次EXTRACT-MIN的执行时间为𝑂 𝑙𝑔 𝑉 ，每次DECREASE-KEY的执行时间为 𝑂 𝑙𝑔 𝑉 。
• 斐波那契堆 𝑶(𝑽 𝒍𝒈𝑽 + 𝑬) 。每次EXTRACT-MIN的摊还代价为𝑂 𝑙𝑔 𝑉 ，每次DECREASE-KEY的摊还代价为𝑂(1)

正确性证明

Dijkstra算法运行在带权重的有向图𝐺 = （𝑉，𝐸） 时，如果所有权重为非负值，则在算法终止时，对于所有结点𝑢 ∈ 𝑉，有 𝑢. 𝑑 = 𝛿 （𝑠, 𝑢） 。

**证明：只需证明对于每个结点𝑢 ∈ 𝑉，当𝑢被加入到𝑆时，有𝑢. 𝑑 = 𝛿 𝑠, 𝑢 。一旦证明了 𝑢. 𝑑 = 𝛿 𝑠, 𝑢 ，就可以使用上界性质（ 对于所有的结点𝑣 ∈ 𝑉，有𝑣. 𝑑 ≥ δ （𝑠, 𝑣） 。一旦𝑣. 𝑑的取值达到𝛿（ 𝑠, 𝑣） ，其值将不再发生变化。）**来证明该等式在后续的所有时间内保持成立。

初始化：初始时𝑆 = ∅，因此循环不变式成立。

保持：

​ 我们希望证明在每次循环中，对于加入到𝑆的结点𝑢来说，𝑢. 𝑑 = δ （𝑠, 𝑢） 。 使用反证法。设𝑢是第一个在加入到𝑆时使得该方程式不成立的结点，即𝑢. 𝑑 ≠ δ（ 𝑠, 𝑢） 。由于结点𝑠是第一个加入到集合𝑆中的结点，并且𝑠. 𝑑 = δ （𝑠, 𝑠） = 0，结点 𝑢必定与结点𝑠不同，即𝑢 ≠ 𝑠。 因为𝑢 ≠ 𝑠，在即将把𝑢加入到𝑆时，有𝑆 ≠ ∅。此时一定存在某条从𝑠到𝑢的路径， 否则将有𝑢. 𝑑 = δ （𝑠, 𝑢） = ∞，而这将违反我们的假设𝑢. 𝑑 ≠ δ （𝑠, 𝑢） 。因为至少存 在一条从𝑠到𝑢的路径，所以也存在一条从𝑠到𝑢的最短路径𝑝。 在将𝑢加入到𝑆之前，路径𝑝连接的是𝑆中的一个结点(即𝑠)和𝑉 − 𝑆中的一个结点 (即𝑢）。考虑𝑝上第一个满足𝑦 ∈ 𝑉 − 𝑆的结点𝑦，设𝑥 ∈ 𝑆为结点𝑦在路径𝑝上的前 驱，可以将路径𝑝分解为𝑠 →𝑝1 𝑥 → 𝑦 →𝑝2 𝑢。(路径𝑝1或者𝑝2可能不包含任何边)

​ 因为选择的结点𝑢是第一个在加入到集合𝑆时𝑢. 𝑑 ≠ δ (𝑠, 𝑢) 的结点，即x满足S的性质故在将结点𝑥加 入到集合𝑆时，有𝑥. 𝑑 = δ (𝑠, 𝑥) 。此时，边 𝑥, 𝑦 将被松弛（算法第7行开始对x的邻点）。因此，在将𝑢加入到𝑆 时，𝑦. 𝑑 = δ （𝑠, 𝑦） 。 现在通过反证法证明𝑢. 𝑑 = δ （𝑠, 𝑢） 。因为𝑦是从𝑠到𝑢的一条最短路径上位于𝑢前面 的一个结点，并且所有的边权重均为非负值，所以有δ （𝑠, 𝑦） ≤ δ （𝑠, 𝑢） ，因此

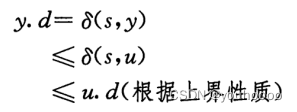
因为在算法第5行选择结点𝑢时，𝑢和𝑦都在集合𝑉 − 𝑆里，所以有𝑢. 𝑑 ≤ 𝑦. 𝑑（前面 我们假设𝑢先于𝑦被抛出）。故

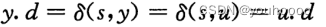
因此𝑢. 𝑑 = δ （𝑠, 𝑢） 。这与我们所选择的结点𝑢矛盾。因此在𝑢被加入到𝑆时有𝑢. 𝑑 = δ （𝑠, 𝑢） ，并且该等式在随后的所有时间内都保持成立。

终止：在算法终止时，𝑄 = ∅，𝑆 = 𝑉，对于所有的结点𝑢 ∈ 𝑉有𝑢. 𝑑 = δ （𝑠, 𝑢） 。

所有节点对的最短路径问题

floyd-warshall算法

采用动规的思想

负权重的边可以存在，但不能存在权重为负值的环路。

时间复杂度：$\Theta (n^3)$

递归公式

设d_ij^(k) 为从节点i到j的所有中间节点全部取自集合{1，2，… , k}的一条最短路径的权重

当 k = 0时，i到j的一条不包括编号大于0的中间节点的路径将没有任何中间节点。这样的路径最多只有一条边。因此，d_ij⁽⁰⁾ = w_ij 。递归定义 d_ij^(k)如下：

$$d_{ij}^{(k)}=\{\begin{array}{l}{w}_{ij},k=0\\ min(d_{ij}^{(k-1)},d_{ik}^{(k-1)}+d_{kj}^{(k-1)}),k\ge 1\end{array}$$

floyd-warshall(w)
n = w.rows
D(0) = w
for k = 1 to n
    let D(k) be a newn*n matrix
    for i = 1 to n
        for j = 1 to n
            dij(k) = min ( dij(k-1) , dik(k-1) + dkj(k-1) )

#include <iostream>
#include <climits>

const int MAX_SIZE = 100;

void floydWarshall(int w[MAX_SIZE][MAX_SIZE], int n) {
    int D[MAX_SIZE][MAX_SIZE];

    // Initialize D(0) with the given matrix w
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            D[i][j] = w[i][j];
        }
    }

    // Main loop of the algorithm
    for (int k = 0; k < n; ++k) {
        int Dk[MAX_SIZE][MAX_SIZE];

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                // Update the shortest path from i to j considering vertex k
                Dk[i][j] = std::min(D[i][j], D[i][k] + D[k][j]);
            }
        }

        // Update D for the next iteration
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                D[i][j] = Dk[i][j];
            }
        }
    }

}

在计算矩阵𝐷 (𝑘)的同时计算前驱矩阵Π

定义𝜋_ij^(𝑘) 为从𝑖到𝑗的一条所有中间结点都取自集合{1,2, … , 𝑘}的最短路径上𝑗的前驱结点。

$${\pi }_{ij}^{(0)}=\{\begin{array}{l}NIL,若i=j或w_{ij}=INF\\ i，若i\ne j且w_{ij}<INF\end{array}$$

对于k$\ge 1$

$${\pi }_{ij}^{(k)}=\{\begin{array}{l}{\pi }_{ij}^{(k-1)},若d_{ij}^{(k-1)}\le d_{ik}^{(k-1)}+d_{kj}^{(k-1)}\\ {\pi }_{kj}^{(k-1)}，若d_{ij}^{(k-1)}>d_{ik}^{(k-1)}+d_{kj}^{(k-1)}\end{array}$$

有向图传递闭包

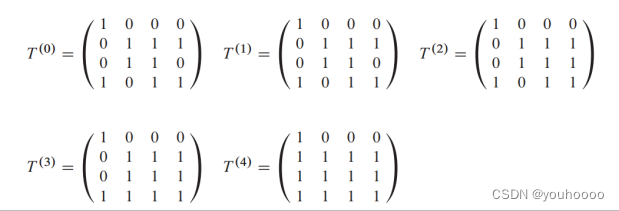
Johnson算法

时间复杂度：$O(V^{2}lgV+VE)$

原因：首先运行了bellman-ford算法，然后对每个结点运行了dijkstra算法

使用的技术

**重新赋予权重。**新赋予的权重满足下面两个性质：

• 1.非负(dijkstra算法的要求)
• 2.对于所有结点对 𝑢, 𝑣 ∈ 𝑉,一条路径𝑝是在使用权重函数w时从𝑢到𝑣的一条最短路径，当且仅当𝑝是在使用权重函数w’时从𝑢到𝑣的一条最短路径（原来是最短路径，重新赋权后还要能找到这一路径）

**方法：**新增一个点，其到各个点有边权重为0（距离为0），再用bellman-ford算法求出各个点到它的距离，然后重新赋予权重。（1.如果不新加点而随机采用原有的点，很可能无法到达其它所有的点 2.如果有负权边，那么其他点到这个新增点的距离就会有变化，否则仍为0）

给定带权重的有向图𝐺 = （𝑉, 𝐸） ，其权重函数为𝑤: 𝐸 → 𝑅，设ℎ: 𝑉 → 𝑅为任意函数，该函数将结点映射到实数上。对 于每条边 （𝑢, 𝑣） ∈ 𝐸，$w’(u,v) = 𝑤 (𝑢, 𝑣) + ℎ(u) − ℎ (𝑣) $

**性质1.证明：**在 Bellman-Ford结束后 任意h（v）< h(u) + w(u,v) ， 得证。

性质2.证明：

算法

11-12行是为了还原出真实距离

​