第六讲 中值和顺序统计问题(Median and Order Statistics)
问题描述:给定n个无序元素,找出其中第i-th小的数.
一个最基本的方法:先排序,然后返回第i个元素,这种方法在使用merge Sort的情况下,时间复杂度为Theta(nlgn);
当i=1时,即变成求最小值(minimum)问题,可以在线性时间内完成;
当i=n时,变成求最大值(maximum)问题,也可以再线性时间内完成;
那么更一般的问题,如求中值(median)问题,最好的时间复杂度是什么??
6.1 随机选择法(RAND-SELECT)
这是一种随机分治法,算法的伪代码如下:
RandSelect(A,p,q,i) //<em>i</em>-th smallest of A[p...q] if p = q then return A[p] r = RandPartition(A,p,q) k = r - p + 1 //k = rank(A[r]) if i = k then return A[r] if i < k then return RandSelect(A,p,r-1,i) else return RandSelect(A,r+1,q,i-k) //find the <em>(i-k)</em>-th value.
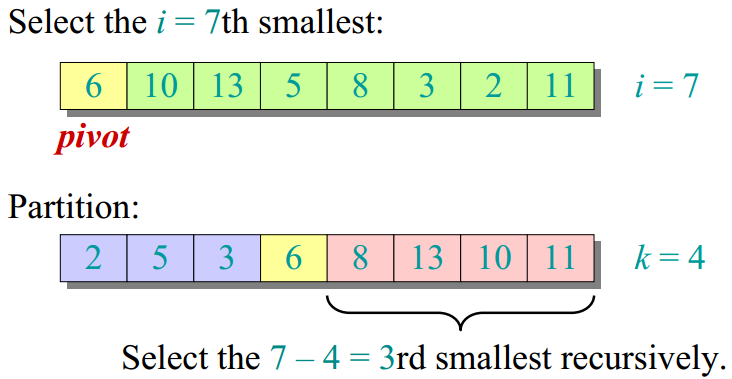
通过如下这个例子,可以更容易理解在最后一个else里面是寻找第(i-k)-th元素,而非第i-th元素,如下图
6.1.1直觉分析(假定所有元素均不同)
这个分析类似于第四讲中对快排的分析,如有兴趣请参照文章《MIT算法导论学习笔记-Lecture4 分治法(续)》,下图仅给出结果:
即,在最坏的情况下该算法的运行时间为Theta(n^2),还不如排序来得快。
6.1.2期望运行时间
考虑到第在第四讲中没有给出随机化快排运行时间为Theta(nlgn)的证明,这里给出RAND-SELECT算法的期望时间复杂度的证明。
两个假设:——T(n)是表示输入n元素时RAND-SELECT算法的运行时间的随机变量;
——假设所有的随机数选择是独立的(这样保证每次调用随机划分时得到的结果独立于其他时候的调用);
一个随机变量:指示器随机变量(indicator random variable),定义如下图:
上述定义的意思是,Xk只在划分为k:n-k-1时的概率为1,其他情况概率为0.
为了得到期望运行时间的上界,我们假设i总是落在划分后元素个数较多的一方,即max(k,n-k-1),如下图:
对上面公式左右求期望,得到:
最后一步推导用到了max(k,n-k-1) = max(n-k-1,k),即由0到n-1,max总是成对出现的,这才有了系数上的2.
我们要证明的是E[T(n)] = Theta(n),即对于一个常数c,有E[T(n)] <= c·n,
采用数学归纳法(induction),可以得到:
在上式的推导中,用到了如下的公式:
我们只要保证红框里的那一项不小于0即可;所以可以通过选择足够大的常数c来获得。
由此即可得到RAND-SELECT算法的运行时间期望为Theta(n),而最坏运行时间为Theta(n^2).
Note:该算法在实际中很好应用,随机划分即和随机化快排的划分相同。
6.1.3 算法C语言实现
// Lecture 6 order stasitics void swap(int *a,int *b) // swap a and b { int temp = *a ; *a = *b ; *b = temp ; } //========6.1 Random Select int RandomPartition(int A[],int p,int q) { int k ; int n = q-p+1 ; // The num of the elements. srand((int)time(NULL)) ; k = rand()%n + p; //Get a random pivot A[k],the index here is [rand()%n + p],not k !!!! int pivot = A[k] ; // Switch A[k] and A[p], then it falls into general partition, so we can use general partition. swap(&A[p],&A[k]) ; int i = p ; for (int j = p + 1;j <= q; j ++) { if (A[j] <= pivot) { i ++ ; swap(&A[j],&A[i]) ; } } swap(&A[p],&A[i]) ; return i ; } int RandomSelect(int A[],int p,int q,int i)//Find the i-th smallest value in A[p,...q]. { if (p == q) { return A[p] ; //Find the i-th smallest num. } int r = RandomPartition(A,p,q) ;//partition int k = r - p + 1;//The rank of element r, namely the position of A[r] after sorting. if (k == i) { return A[r] ; } else if (i < k) { return RandomSelect(A,p,r-1,i) ;//Find the i-th element in the smaller half. } else { return RandomSelect(A,r+1,q,i-k) ;//Find the (i-k)-th element in the greater half, NOTE that the index changed. } }
6.2最坏情况线性时间顺序统计方法(Worst-caselinear time order statistics)
6.2.1 算法分析
——思想:选择好的主元(pivot)。
注:该方法的作者是Blum, Froyd, Pratt, Rivest, Tarjan,一群大牛,谷歌学术直接搜索这几个名字可以得到该算法的文章。
该方法的步骤:
1 把n个元素每5个一组进行划分,并且找到每一组的中值;
2 递归地选择所有的中值(一共是Floor(n/5)个元素)的中值x来当主元;
3 围绕x进行划分,并且另k作为x划分后的位置,即k=rank(x);
4 如果i = k,则返回x
Else if i<k
则递归地在较小的一部分中选择第i小的数;
Else
则递归地在较大的一部分中选择第i-k小的数;
在上述步骤中,第三步和第四步其实是与随机选择法完全相同。
该方法的证明可以参考课件、视频或者直接看文章,这里不再给出,但是视频里说到一个思想我认为是及其重要的,即:要想在分治法中得到线性的时间复杂度,则问题的子问题的size要小于n,即如下
T(n)= T(k) + Theta(n), k<n
6.2.2 算法C语言实现
//========6.2 Worst-Case linear time order statistics. void swap(int *a,int *b) // swap a and b { int temp = *a ; *a = *b ; *b = temp ; } int Partition(int A[],int p,int q,int mid) { int pivot = mid ; int n = q - p + 1; int *aux = (int *)malloc(n*sizeof(int)) ; int i = p, j = q ; for (int k = p; k <= q; k ++) { if (A[k] < mid) { aux[i-p] = A[k] ; //Note that the index of aux[] is not i,but i-p,same case with j !!!!! i ++ ; } if (A[k] > mid) { aux[j-p] = A[k] ; j -- ; } } for (int k = i; k <= j; k ++) { aux[k-p] = mid ; } for (int k = p; k <= q; k ++) { A[k] = aux[k - p] ; } free(aux) ; return j ; } //Sort 5 elements, and return the median. int GetMid(int A[],int p,int q) { //insertion sort. int i,j ; for(i = p + 1;i <= q; i++ ) { int temp = A[i] ;// it would be overlaid. if(A[i] < A[i-1]) { j= i -1 ; while(j >= p && temp <= A[j]) { A[j+1] = A[j] ; j -- ; } A[j+1] = temp ; } } return A[(p+q+1)/2] ; } int Select(int A[],int p, int q, int i) { if (p == q) { return A[p] ; } // partition the elements into groups, with each group contains 5 elements. int n = q - p + 1 ; // the num of the elements. int groups = (n + 4)/ 5 ; // This can get the Ceil(n/5). int *pmid ; //Store the median of each group in this array. pmid = (int *)malloc(groups*sizeof(int)) ; // Get the mid elements. int g_beg,g_end ; int j ; for (j = 0; j < groups - 1; j ++) { g_beg = j*5 + p; g_end = g_beg + 4 ; // pmid[j] = GetMid(A,g_beg,g_end) ; } //The last group may be less than 5 elements g_beg = (groups - 1)*5 + p; g_end = q ; pmid[j] = GetMid(A,g_beg,g_end) ; // Get the mid of the medians. int mid = GetMid(pmid,0,groups-1) ; // free pmid. free(pmid) ; int r = Partition(A,p,q,mid) ;//partition int k = r - p + 1;//The rank of element r, namely the position of A[r] after sorting. if (k == i) { return A[r] ; } else if (i < k) { return Select(A,p,r-1,i) ;//Find the i-th element in the smaller half. } else { return Select(A,r+1,q,i-k) ;//Find the (i-k)-th element in the greater half, NOTE that the index changed. } }6.2.3 关于第i-th问题和中值问题
关于第i-th问题和中值问题,其他博客也有介绍:
下面的这个博客,我认为讲的更加清晰有条理:








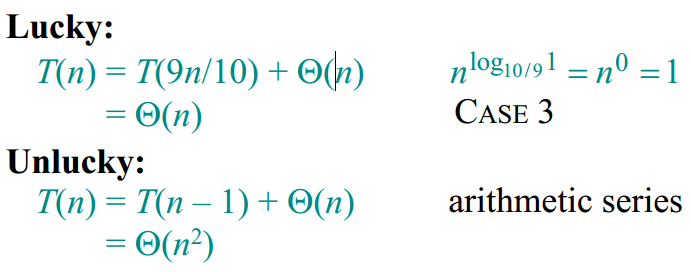
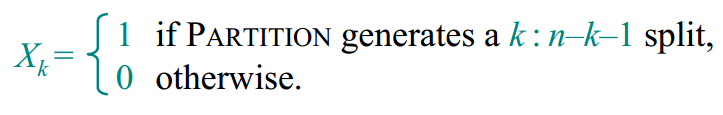
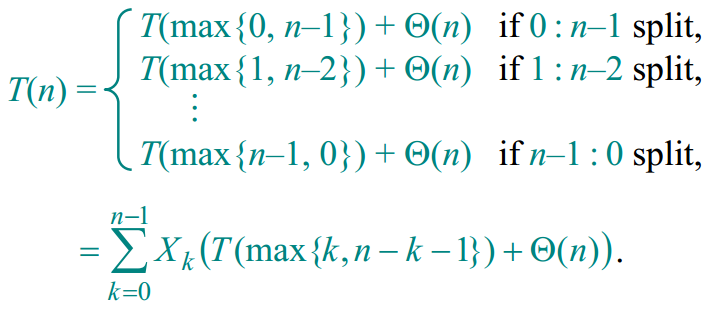

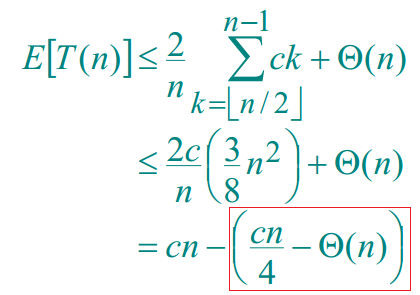
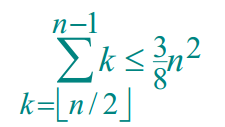















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








