【NOI2007】货币兑换

今天听了crazy和samjia的NOI杂（砸）题选讲，感觉自己萌萌哒~
于是就来怡情地写了这道题。

Description

额(⊙o⊙)…，这个不好说啊。（语文不好不好裱我）
还是贴图吧。


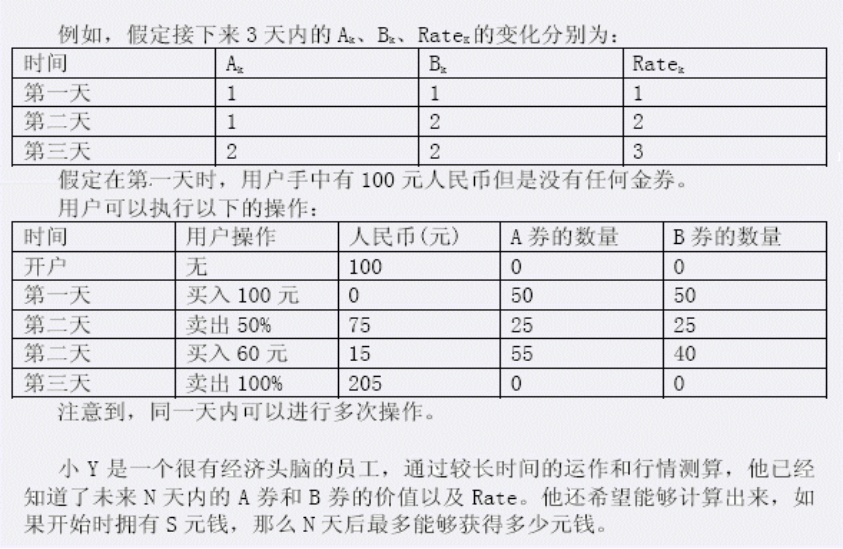
n<=10^5

Solution

咳咳，希望大家都看懂题了。
一个很明显的贪心思路就是，我们每天要不全买，要不全卖。
因为一有利益我们就去占，一有亏损我们就不碰。
那么我们可以有dp方程：

$$F[i]=max(x[j]*a[i]+y[j]*b[i],F[i-1])$$
因为你一天可以什么都不淦。
其中x[i]表示第i天最多能获得的A卷数量，y[i]表示B卷数量。
那么 $$x[i]=F[i]/(A[i]*Rate[i]+B[i])*Rate[i]$$
$$y[i]=F[i]/(A[i]*Rate[i]+B[i])$$
这样Dp是N^2的，我们考虑优化。
设j是最优决策，那么 $$F[i]=x[j]*a[i]+y[j]*b[i]$$
于是 $$y[j]=-{a[i]\over b[i]}x[j]+{F[i]\over b[i]}$$
发现这是一次函数的形式。我们想让截距最大。
于是我们可以维护一个凸包，因为斜率一定，使截距最大的点一定在凸包上。
以x为x轴，y为y轴建立平面直角坐标系。
但是，x[i]和-a[i]/b[i]不见得单调。
所以我们就是要动态维护一个凸包，然后求某个斜率的位置。
splay大法好！splay大法好！splay大法好！
你每次找到i左边最后一个斜率使得它仍然递增的点，和右边第一个使得它递增的的点。
然后删点就好了。不要忘了判断加上这个点后是否还是凸包。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define N 100005
using namespace std;
typedef double db;
const db inf=0x7fffffff;
const db ep=1e-5;
int n,fa[N],t[N][2],root;
db f[N],x[N],y[N],a[N],b[N],r[N],lk[N],rk[N];
int son(int x) {
    if (t[fa[x]][0]==x) return 0;else return 1;
}
void rotate(int x) {
    int y=fa[x],z=son(x);fa[x]=fa[y];
    if (fa[y]) t[fa[y]][son(y)]=x;
    if (t[x][1-z]) fa[t[x][1-z]]=y;
    fa[y]=x;t[y][z]=t[x][1-z];t[x][1-z]=y;
}
void splay(int x,int y) {
    while (fa[x]!=y) {
        if (fa[fa[x]]!=y)
            if (son(x)==son(fa[x])) rotate(fa[x]);
            else rotate(x);
        rotate(x);
    }
    if (!y) root=x;
}
void insert(int &v,int f,int id) {
    if (!v) {v=id;fa[v]=f;splay(v,0);return;}
    if (x[id]<=x[v]+ep) insert(t[v][0],v,id);
    else insert(t[v][1],v,id);
}
db getk(int i,int j) {
    if (abs(x[j]-x[i])<ep) return -inf;
    else return ((y[j]-y[i])/(x[j]-x[i]));
}
int pre(int x) {
    int y=t[x][0],z=x;
    while (y)
        if (getk(y,x)<=lk[y]+ep) z=y,y=t[y][1];
        else y=t[y][0];
    return z;
}
int suc(int x) {
    int y=t[x][1],z=x;
    while (y)
        if (getk(x,y)+ep>=rk[y]) z=y,y=t[y][0];
        else y=t[y][1];
    return z;
}
void updata(int x) {
    splay(x,0);
    if (t[x][0]) {
        int left=pre(x);splay(left,x);t[left][1]=0;
        lk[x]=rk[left]=getk(left,x);
    } else lk[x]=inf;
    if (t[x][1]) {
        int right=suc(x);splay(right,x);t[right][0]=0;
        rk[x]=lk[right]=getk(x,right);
    } else rk[x]=-inf;
    if (lk[x]<=rk[x]+ep) {
        root=t[x][0];t[root][1]=t[x][1];
        fa[t[x][1]]=t[x][0];fa[x]=0;
        rk[root]=lk[t[root][1]]=getk(root,t[root][1]);
    }
}
int find(int v,db k) {
    if (!v) return 0;
    if (lk[v]+ep>=k&&k+ep>=rk[v]) return v;
    if (k>lk[v]) return find(t[v][0],k);
    else return find(t[v][1],k);
}
int main() {
    scanf("%d%lf",&n,&f[0]);
    fo(i,1,n) scanf("%lf%lf%lf",&a[i],&b[i],&r[i]);
    fo(i,1,n) {
        int j=find(root,-a[i]/b[i]);
        f[i]=max(f[i-1],x[j]*a[i]+y[j]*b[i]);
        y[i]=f[i]/(a[i]*r[i]+b[i]);
        x[i]=y[i]*r[i];
        insert(root,0,i);
        updata(i);
    }
    printf("%.3lf",f[n]);
}