随机过程：【1】基于MATLAB对泊松过程的仿真与数字特征的验证

最近刚好完成了学校里随机过程专业课的大作业，想着还从来没有发过一篇正式的博客，就把这个当成养成写博客好习惯的开头吧。希望可以给读者一定的启示。

P.S. 如果后续有学弟学妹看到这篇文章的话，希望能够给大家一些小小的启示~同时由于本人能力实在有限，希望大家能够指出我的错误，大家共同进步~

                  目录

一.概念原理

二.实现步骤

三.实验结果

四.结论

五.源代码

---

一.概念原理

首先我们需要回顾一下计数过程以及泊松过程的定义，将对代码的书写有着至关重要的作用。

• 计数过程

• 泊松过程定义1

• 泊松过程定义2

•  泊松过程的数字特征

二.实现步骤

由于MATLAB中具有自带生成泊松随机数的random函数，可以按照以下格式产生服从特定参数的泊松随机数。

random('Poisson',lambda）

基于上述的办法，整体思路如下：

三.实验结果

任意一次样本函数展示如下，可以发现,基本符合泊松过程样本函数的特点，呈现一个具有随机性的阶梯状。

利用MATLAB仿真程序所得到的数据，分别计算了不同样本函数数量，时间间隔大小， lambda 对样本均值函数和方差函数的影响，并对不同样本集的均值函数、方差函数与理论 值进行了对比，并计算了两者与理论值之间的线性相关系数。不同样本集的数据分布和他们的均值函数、方差函数与理论值（𝜆𝑡）的对比如下，可发现理论值和真实值基本吻合，且相关性很好。

注：图 4 为图 3 的局部放大图，因图 3 出现数据线的重叠现象。 

• 样本函数数量 = 100、 时间间隔 T=1、 𝝀=10

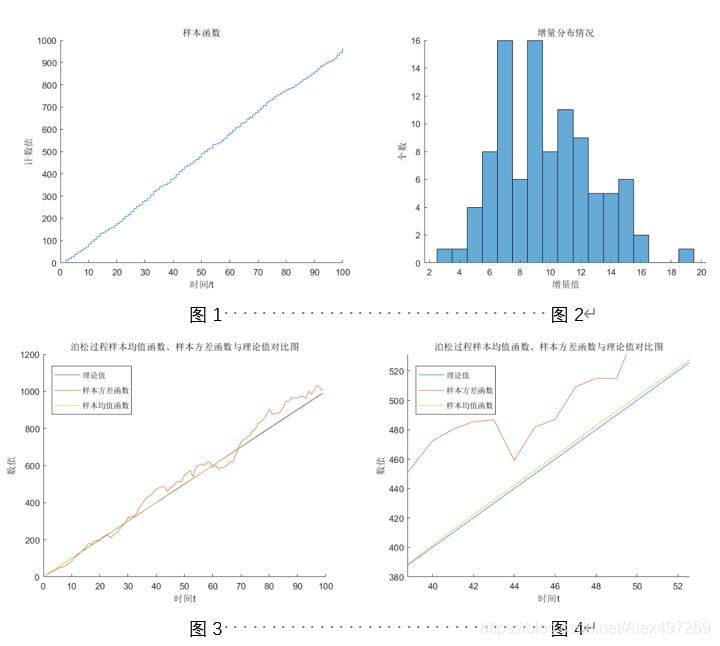
进行比较的曲线	相关系数
理论值与样本方差函数	0.995209665496913
理论值与样本均值函数	0.999996538503252

• 样本函数数量 = 1000、 时间间隔 T=1、 𝝀=10

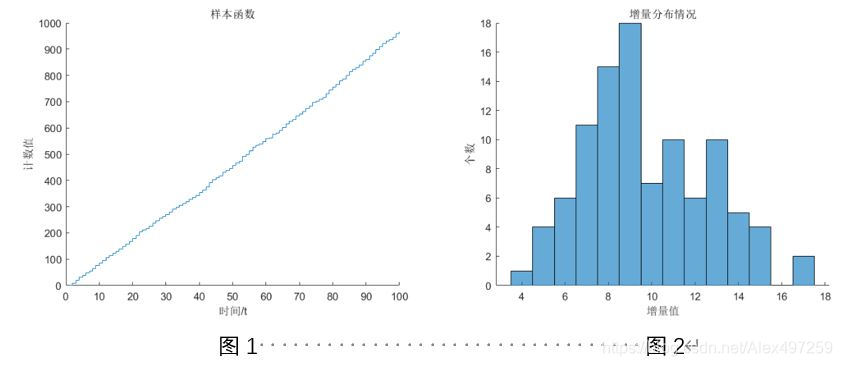
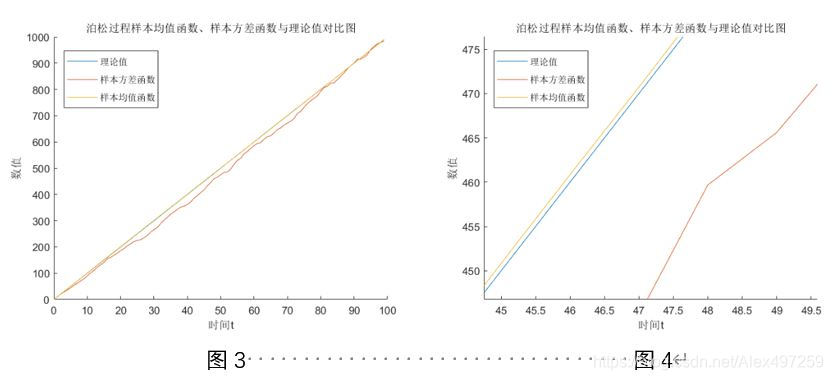
进行比较的曲线	相关系数
理论值与样本方差函数	0.999214626772327
理论值与样本均值函数	0.999999392860723

• 样本函数数量 = 10000、 时间间隔 T=1、 𝝀=10

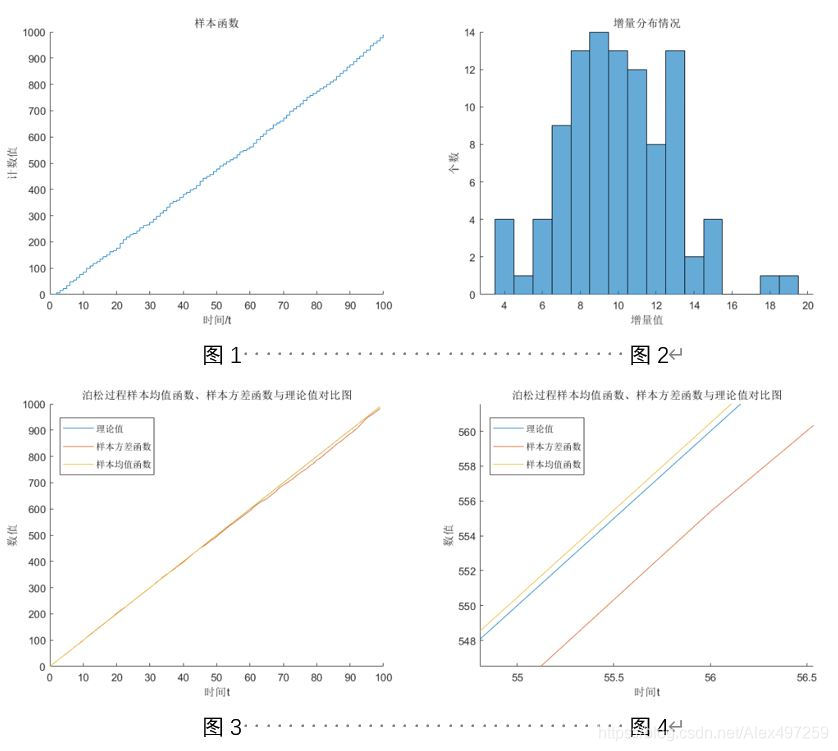
进行比较的曲线	相关系数
理论值与样本方差函数	0.999937944446522
理论值与样本均值函数	0.999999941351360

• 样本函数数量 = 1000、 时间间隔 T=2、 𝝀=10

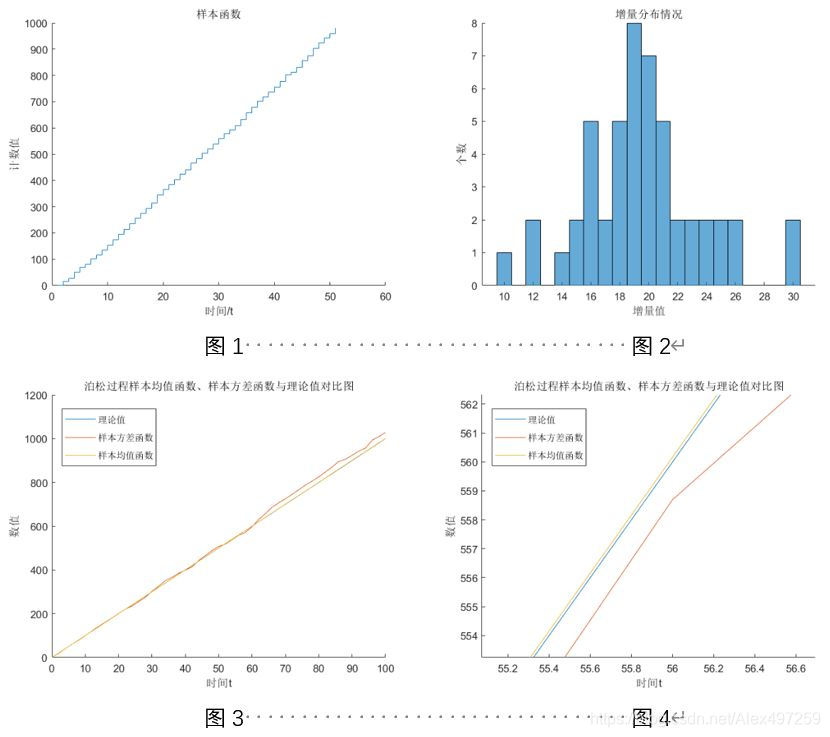
进行比较的曲线	相关系数
理论值与样本方差函数	0.999691706642537
理论值与样本均值函数	0.999999838156047

• 样本函数数量 = 1000、 时间间隔 T=1、 𝝀=30

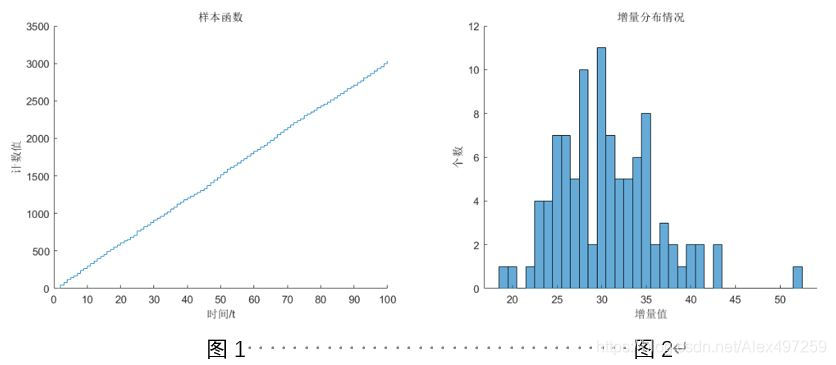
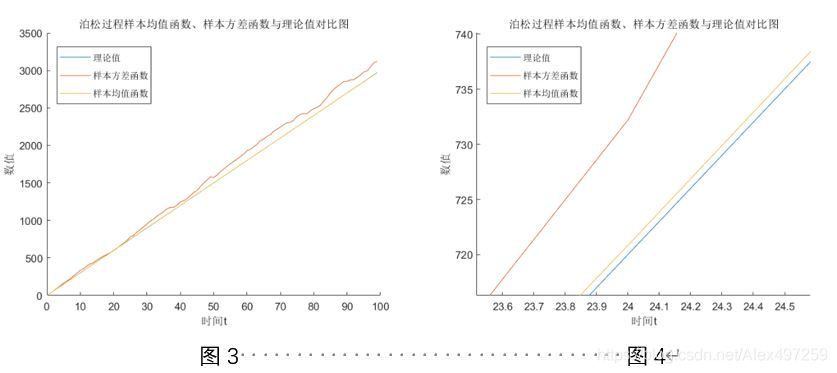
进行比较的曲线	相关系数
理论值与样本方差函数	0.998571520503543
理论值与样本均值函数	0.999999857436511

基于上述实验的基础，在样本函数数量 = 10000、 时间间隔T=1、 λ=10 的情况下

进一步计算了样本的均方值函数值，自相关函数值，自协方差函数值，图像如下，可发现理论值和真实值基本吻合，且相关性很好。

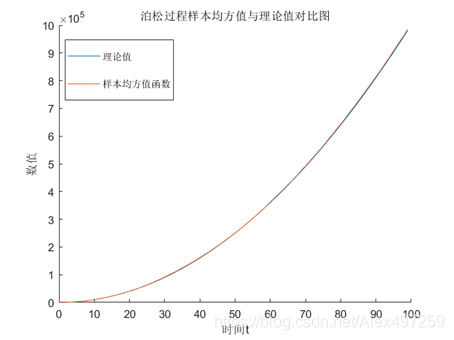
进行比较的曲线	相关系数
理论值与样本均方值函数	0.999997709686615
理论值与自相关函数	0.999997397175130
理论值与样本自协方差函数	0.999928631593560

 四.结论

• 初步验证了泊松过程的数学特征，其样本的均值函数和方差函数满足以下等式：

• 经过分析实验结果，得知当样本函数数量增加时，样本的均值函数和方差函数与理论值的拟合效果更好，同时λ与时间间隔T对相关系数的影响不大。

五.源代码

下载地址：随机过程：【1】基于MATLAB对泊松过程的仿真与数字特征的验证.zip-电信代码类资源-CSDN下载

• 代码调用界面

• PoissonProcess.m

function [result,time,expected,average,variance] = PoissonProcess(TestNumber,lamda,TimeMAX,T)
%UNTITLED4 此处显示有关此函数的摘要
%   此处显示详细说明
%   TestNumber样本函数个数
%   lambda
%   TimeMAX最后的时间值
%   T代表时间间隔
%   result为结果，每行为一个样本
%   time为真实时刻
%   expected为方差和均值的预测值
%   average为样本函数均值
%   variance为样本函数方差
t = 2; %代表实际的时间
TimeMAX = TimeMAX + T ; %偶数 完全对
for TestCount = 1:TestNumber 
    clear average JIA JIA_graph  N N_graph number q x x_graph Zengliang;
    N(1) = 0;
    N(1 + T)=random('Poisson',T*lamda);
    JIA(1) = N(1 + T) - N(1);
    t = 1 + T;
    while(t < TimeMAX)
        Zengliang = random('Poisson',T*lamda);
        N(t+T) = N(t) + Zengliang;
        JIA(t) = Zengliang; %JIA（i）用来存储从（i）到（i+1） 的增量
        t = t + T;
    end
    %去除含有的0;
    q = 1 + T;
    x = 2;
    N_graph(1) = 0;
    JIA_graph(1) = JIA(1);
    while(q < TimeMAX)
        N_graph(x) = N(q);
        JIA_graph(x) = JIA(q);
        q = q + T;
        x = x + 1;
    end
    number = x - 1;
    result(TestCount,:) = N_graph;
end
time = (0:T:T*(size(result,2)-1)); %时刻
average = mean(result(1:TestCount,:)); %时刻对应的平均值
variance = var(result(1:TestCount,:)); %时刻对应的方差
expected = time.*lamda; %lamba*t
end

• ResultShow.m

function [Pearson1, Pearson2] = ResultShow(result,time,expected,average,variance)
%UNTITLED7 此处显示有关此函数的摘要
%   1 展示一个样本函数
figure1 = figure;
axes1 = axes('Parent',figure1);
hold(axes1,'on');
stairs(result(1,:));
title({'样本函数'});
ylabel({'计数值'});
xlabel({'时间/t'});
%   2 展示样本分布
for(i = 1: size(result,2) - 1)
    JIA(i) = result(1,i+1) - result(1,i);
end
figure2 = figure;
axes2 = axes('Parent',figure2);
hold(axes2,'on');
histogram(JIA);
title({'增量分布情况'});
ylabel({'个数'});
xlabel({'增量值'});
%   3 展示样本的理论值，均值，方差
figure3 = figure;
axes3 = axes('Parent',figure3);
hold(axes3,'on');
plot(time,expected);
plot(time,variance);
plot(time,average);
ylabel({'数值'});
xlabel({'时间t'});
title({'泊松过程样本均值函数、样本方差函数与理论值对比图'});
legend('理论值','样本方差函数','样本均值函数');
legend1 = legend(axes3,'show');
set(legend1,...
    'Position',[0.177395983388902 0.705548654244307 0.17127696712065 0.178743961352668]);
%   4 计算相关系数
Pearson1 = corrcoef(average,expected);
Pearson2 = corrcoef(variance,expected);
end

• PoissonPlus.m

function [Pearson3,Pearson4,Pearson5]=PoissonPlus(result,time,average,lambda)
% 此函数用来完成拓展任务，进一步验证余下的三个数字特征
% 该部分请下载资源