Leetcode Super Ugly Number

题目

写一个程序查找第n个super ugly number.
一个super ugly number 是所有质数由给定列表中的质数构成的正整数。比如，对给定的素数列表：primes = [2, 7, 13, 19]，前12个super ugly number是[1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32]

思考

反正我自己是没琢磨出来。之前我看过一次geeks4geeks上的解释，那会看明白了，但自己其实还是没掌握思考出这个方法的那些灵感点。所以这次再打算做，又忘了，然后自己琢磨也没琢磨出来。大概方向大概是知道的：每个super ugly number都是之前的某个super ugly number 乘以primes中的某个prime number生成的。问题在于我们不能一直保存所有历史信息，否则不止占据内存，而且计算的时候要检查所有历史的值*某个prime数，效率也会很低。那么我们怎么知道保存到前面什么时候就可以了呢？没找出来。

实际算法还是挺简单的写起来，大家看一下都可以明白。问题就是其实不太明白为什么这样就是正确的。然后我找到了一个SO的提问，看下面的回答才知道原来这个生成方式也是有来源的。那个解法居然是Dijkstra提出来的。

然后这个问题是叫做regular number的一种算法，见维基百科页面。

然后这里有一份Dijkstra的手稿，证明为什么这个算法是正确的：http://www.cs.utexas.edu/users/EWD/ewd07xx/EWD792.PDF 看这份证明，因为是草稿形式的，有些符号第一眼看过去不知道想表达什么，还好有看TAOCP的经验，结合后面的部分看明白了作者是用冒号表示一个序列的连接，好多定义颇有点functional programming范式的感觉（头/尾递归）。其实蛮美妙的感觉，看他这么去定义一些东西但到了真正关键的证明的那步，总有点“就这样，然后这样”理所当然的感觉。

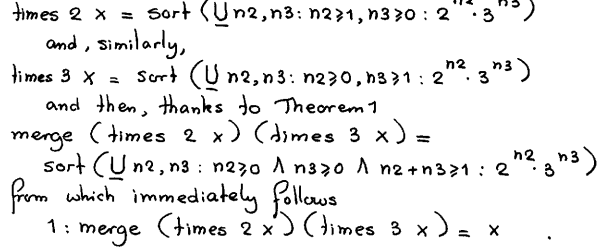
这里merge的定义如下：

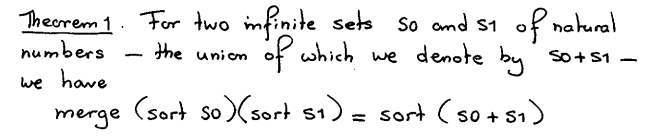
S0+S1中的加号表示Union，所以重复的部分只有一份出现。

总之我现在的感觉还是一种好像很有道理，但又没说到什么道理的茫然。。

代码实现

int nthSuperUglyNumber(int n, vector<int>& primes) {
    int sz = primes.size();
    vector<int> idxs(sz, 1);
    // 正常速度了，100ms，前90.26%
    vector<int> v(n + 1);v[1] = 1;
    for (int i = 2;i <= n;i++) {
        int m = INT_MAX;
        for (int j = 0;j < sz;j++) {
            if (v[idxs[j]] * primes[j] < m) {
                m = v[idxs[j]] * primes[j];
                v[i] = m;
            }
        }
        for (int j = 0;j < sz;j++) {
            if (m == v[idxs[j]] * primes[j]) {
                idxs[j] = idxs[j] + 1;
            }
        }
    }
    return v[n];
}

我这个方法只有100ms时间，排在90.26%，有位仁兄用的c，好像29ms。。然而我按照他那个核心思想修改代码，运行时间并没有什么不同，估计是CPP的vector开销吧。