【论文+代码】基于transformer的端到端符号回归算法_transformer端到端符号回归开源-CSDN博客

本文链接：https://blog.csdn.net/allein_STR/article/details/145000069

✅作者简介：双一流博士，人工智能领域学习者，深耕机器学习，交叉学科实践者。已发表SCI1/区top论文10+，发明专利10+。可提供论文服务，代码复现，专利思路和指导，提供科研小工具，分享科研经验，欢迎交流！
📌个人主页： https://blog.csdn.net/allein_STR?spm=1011.2559.3001.5343
📞联系博主：博文留言+主页底部联系方式+WeChat: Allein_STR
📙本文内容：【基于transformer的端到端符号回归算法】

1. 研究目的

通过端到端的方式直接预测完整的数学表达式，包括常数，以提高符号回归的效率和准确性。

2. 方法优点

• 端到端预测：传统的符号回归方法通常分为两步：首先预测表达式的骨架，然后拟合常数。而端到端方法直接预测完整的数学表达式，包括常数，避免了中间步骤带来的误差和复杂性。

• 推理速度显著提升：在基准测试中，该方法的推理速度比最先进的遗传编程方法快几个数量级。

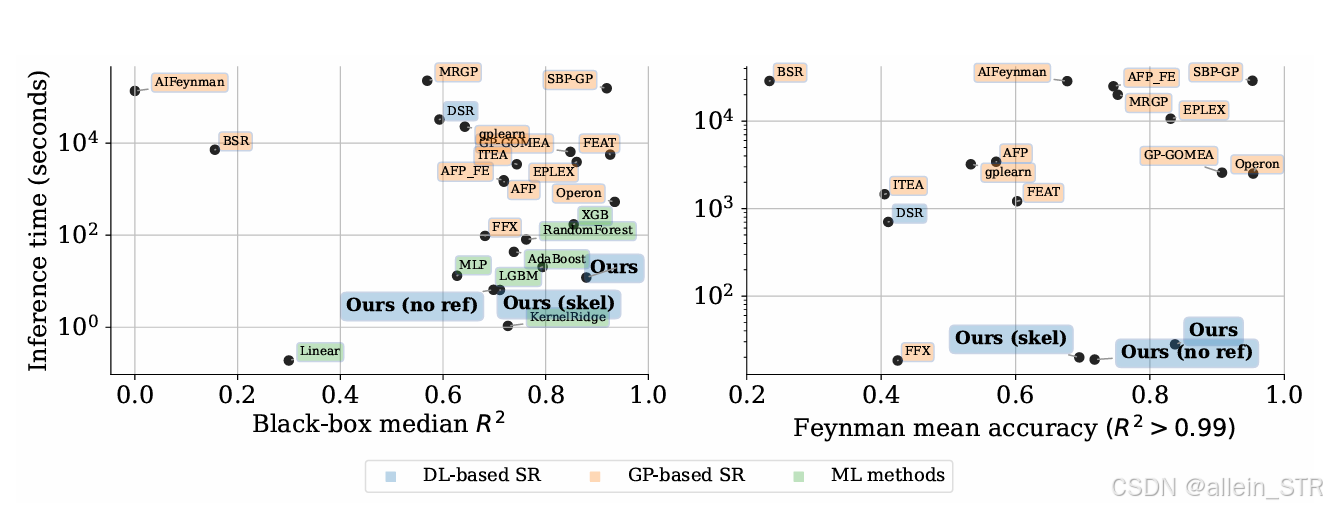
图1：与其他方法精度对比结果。三种颜色表示三种模型系列：基于深度学习的 SR、基于遗传编程的 SR 和经典机器学习方法（不提供可解释的解决方案）。

• 预测准确：Transformer模型因其自注意力机制在处理序列数据时表现出色，能够更好地捕捉输入数据的复杂特征和模式，使得模型在符号回归任务中能够更准确地预测数学表达式（如图1）.

• 改进的预测常数方法：通过将预测的常数作为初始估计值输入到非线性优化器（如BFGS）中，可以对预测的常数进行细化，从而缓解非线性优化问题，减少了陷入局部最优解的风险。

• 鲁棒性：该方法在面对噪声和外推任务时表现出良好的鲁棒性，在输入数据发生变化的情况下仍然保持较高的预测精度，对实际应用中的数据变化和不确定性具有重要意义.

• 外推能力：作者引入了生成和推理技术，使得模型能够处理更大的问题，支持多达10个输入特征，而之前的工作仅限于3个输入特征.

• 公式复杂度低：生成的公式较为简单，可解释性强

图2：与其他方法生成的公式复杂度的对比结果。

3. 模型架构

图3：模型架构

3.1 Embedder

作者介绍了一种用于处理输入数据的嵌入器（embedder），以应对输入序列长度过长的问题，因为Transformer在处理长序列时计算量巨大.。

3.1.1 具体实现方法

填充空维度：嵌入器首先将空的输入维度填充到最大维度Dmax。这一步是为了统一输入点的维度，使其能够被后续的网络处理.
全连接前馈网络（FFN）：填充后的输入点被送入一个具有ReLU激活的2层全连接前馈网络（FFN）。该网络的输入维度为 $eq?3%28D_%7Bmax%7D+1%29d_%7Bemb%7D$ ，输出维度为 $eq?d_%7Bemb%7D$ 。通过这个FFN，模型能够将每个输入点的高维表示压缩为一个低维的嵌入向量.
输出嵌入：最终，得到的N个 $eq?d_%7Bemb%7D$ 维嵌入向量被输入到Transformer模型中进行后续处理.

3.1.2 嵌入器的作用与意义

降低计算复杂度：通过将每个输入点映射到一个单独的嵌入，嵌入器有效地减少了输入序列的长度，从而降低了Transformer模型的计算复杂度，使其能够更高效地处理大规模的输入数据.
保留关键信息：尽管嵌入器对输入数据进行了压缩，但它仍然保留了输入点的关键信息，使得Transformer模型能够在此基础上进行有效的符号回归任务.
适应性：嵌入器的设计使得模型能够适应不同维度和规模的输入数据，增强了模型的灵活性和鲁棒性.

3.2 Transformer

3.2.1 Transformer模型架构

序列到序列架构：作者采用了序列到序列（sequence-to-sequence）的Transformer架构，这种架构适用于处理输入序列并生成对应的输出序列，非常适合符号回归任务，因为输入是一系列数据点，输出是对应的数学表达式序列.
注意力头和嵌入维度：模型包含16个注意力头和512维的嵌入。注意力头的数量和嵌入维度的选择使得模型能够捕捉输入数据中的复杂模式和关系，同时保持足够的计算能力来处理大规模问题.
参数规模：整个模型共有8600万（86M）个参数，这表明模型具有较高的容量，能够学习丰富的特征表示和复杂的映射关系，从而在符号回归任务中取得更好的性能.

3.2.2 编码器和解码器设计

不对称架构：具体来说，编码器有4层，而解码器有16层。这种设计是由于符号回归任务中，解码过程需要更复杂的操作来生成准确的数学表达式，因此更深的解码器能够提供更强的建模能力.
编码器的排列不变性：由于输入点的顺序不影响最终的数学表达式，模型具有排列不变性。为了适应这种不变性，作者从编码器中移除了位置嵌入（positional embeddings）。这使得编码器能够更好地捕捉输入数据的内在特征，而不是依赖于输入点的顺序信息.

3.2.3 编码器的功能和特点

捕获关键特征：编码器能够捕获输入函数的最显著特征，如临界点和周期性。这得益于其设计中混合了关注局部细节的短程头和捕获函数全局形状的长程头。这种多尺度的分析能力使得模型能够全面理解输入数据的特性，为后续的表达式生成提供坚实的基础.
自注意力机制：编码器中的自注意力机制使得模型能够在不同输入点之间建立联系，发现数据中的相关性和模式。例如，对于周期性函数，模型可以通过自注意力分析输入点之间的周期性关系，从而更好地理解和建模这种特性.

3.3 训练策略

优化器和学习率调度：模型使用Adam优化器来优化交叉熵损失，并采用学习率预热和衰减策略。学习率从10^-7逐渐增加到2×10^-4，经过前10,000步，然后随着步数的平方根倒数而衰减。这种策略有助于模型在训练初期快速收敛，并在后期保持稳定的优化过程.
验证集和批量处理：作者从相同的生成器中留出10^4个示例作为验证集，并训练模型直到验证集上的准确率饱和。此外，为了避免浪费填充，模型将相似长度的示例分批处理，确保一个完整的批次包含至少10,000个标记。这种批量处理策略提高了训练效率，同时保证了模型在不同长度的输入数据上都能获得良好的性能.

3.4 模型输入/输出

输入数据：模型的输入是 N 个输入点(x,y)∈R^(D+1)，每个输入点由 D 维的特征 x 和对应的函数值 y 组成。
输入表示：每个输入点被表征为 d_emb 维度的 3(D+1)个 token，以适应 Transformer 模型的输入格式。
输出数据：模型的输出是预测的数学表达式，包括表达式中的符号和常数。
输出表示：输出的数学表达式被表示为一个序列，其中包含符号和数值的混合词汇表，符号包括操作符和变量，数值则以浮点数的形式表示。

3.5 映射方法

自注意力机制：模型利用自注意力机制来捕捉输入序列中不同位置之间的关系，通过多头自注意力机制可以同时关注到输入序列中不同位置的信息。
前馈神经网络：在编码器和解码器的每个层中，自注意力机制的输出会经过前馈神经网络进一步处理，以获得更丰富的特征表示。
位置编码：由于 Transformer 模型本身不具备处理序列顺序的能力，因此通过位置编码将序列中的位置信息注入到输入数据中，使得模型能够捕捉序列中的相对位置关系。
残差连接和层归一化：模型在每个子层模块后都会进行残差连接和层归一化操作，以避免深度网络的梯度消失问题，保证梯度可以顺畅传播到底层

4. 3个小技巧

4.1 Refinement（精细化）

背景：以往的基于Transformer的语言模型在符号回归任务中，通常采用骨架（skeleton）方法，即先预测方程的骨架，然后使用非线性优化求解器（如BFGS）来拟合常数。本文作者采用端到端（E2E）方法，同时预测函数和常数值。
方法：作者通过添加一个精细化步骤来提升结果：使用BFGS对模型预测的常数进行后处理优化，以模型预测的常数作为初始值。这比骨架方法有显著提升。
结果：如表1和表2所示，E2E方法在低精度预测（R2和Acc0.1指标）上优于骨架模型，但在高精度（Acc0.001指标）上稍逊。精细化过程显著改善了这一问题，使Acc0.001指标提高了三倍，同时提升了其他指标。使用E2E阶段估计的常数初始化BFGS至关重要，随机初始化会降低E2E性能。

4.2 Scaling（缩放）

背景：在训练期间，所有输入点都进行了白化处理，即分布以原点为中心且具有单位方差。为了使模型能够准确预测具有不同均值和方差的输入点，作者在推理时引入了缩放。
方法：设f为待推断的函数， $eq?x$ 为输入点，µ为 $eq?x$ 的均值，σ为 $eq?x$ 的标准差。作者通过替换 $eq?x$ 为 $eq?%5Ctilde%7Bx%7D%3D%5Cfrac%7Bx-%5Cmu%20%7D%7B%5Csigma%20%7D$ 来预处理输入数据。模型预测 $eq?%5Chat%7Bf%7D%28%5Ctilde%7Bx%7D%29%3D%5Chat%7Bf%7D%28%5Csigma%20x+%5Cmu%20%29$ ，然后通过在 $eq?%5Chat%7Bf%7D$ 中取消缩放变量来恢复 $eq?f$ 的近似值。
优势：这使得模型对输入点的尺度不敏感，解决了DL在SR中当输入超出训练期间看到的值范围时失败的问题。输入的尺度转换为函数f中常数的尺度；尽管这些系数在训练期间从Daf中采样，但Daf之外的系数可以通过Daf中的常数相乘来表示。

4.3Bagging and Decoding（自助法和解码）

背景：由于模型在N ≤ 200个输入点上进行训练，因此在推理时面对超过200个输入点时表现不佳。为了利用大型数据集同时考虑内存限制，作者采用了自助法。
方法：当N在推理时大于200时，作者将数据集随机分成B个包含200个输入点的包。对于每个包，应用前向传递并通过随机抽样或使用下一个标记分布的束搜索生成C个函数候选。由于束搜索策略在作者的设置中导致多样性低的候选结果，因此采用随机抽样。
结果：这为作者提供了一组BC个候选解。由于BC可能变得很大，作者根据所有输入点上的误差对候选函数进行排名，去除冗余的骨架函数，并保留最佳的K个候选函数进行精细化步骤。为了加快精细化速度，作者在优化中使用了最多1024个输入点的子集。参数B、C和K可以用作速度-精度权衡的游标，在图1中展示的实验中，作者选择了B = 100，C = 10，K = 10。