[LeetCode] Set Matrix Zeroes

前言

Set Matrix Zeroes，一道LeetCode中十分经典的数组题，据说在笔试中出现频率不低。不过此题本质不难，要做到不使用额外空间就稍微要多想一下了。

题目

https://leetcode.com/problems/set-matrix-zeroes/
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place.
Follow up:
Did you use extra space?
A straight forward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?

分析

使用额外空间的话，这题相当简单，设置两个数组，分别记录某行以及某列是否有零，然后在第二次遍历的时候设置一下就行。
问题是O(1)的空间复杂度该如何实现？那就是直接使用原数组的第一行和第一列来记录某一行某一列是否有零的信息——如果第i行第j列的元素为零，那么就把第i行第零列和第零行第j列设为零，这相当于把这个元素为零的信息投影在了最左和最上方的坐标轴上。然后，在第二次遍历中从右下角倒着来，只要遇到了某个元素对应在坐标轴上的投影记录为零，那么就设置它的值为零。

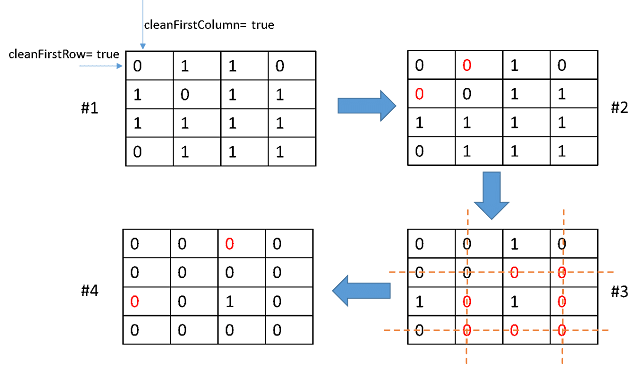
图片来自http://fisherlei.blogspot.com/2013/01/leetcode-set-matrix-zeroes.html

那么第一行(matrix[0][j] )和第一列(matrix[j][0])又该怎么办？我们可以用两个数，col0haszero和row0haszero来记录在第一行和第一列是否有零存在，在设置完矩阵中央的元素之后设置一下就行。

代码

Time complexity: O(m*n), space complexity: O(m+n)

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
      const size_t m = matrix.size();
      const size_t n = matrix[0].size();
      vector<bool> row(m, 0);
      vector<bool> col(n, 0);

      for (size_t i = 0; i < m; i++) {
        for (size_t j = 0; j < n; j++) {
          // Traverse for once and set bool vector
          if (matrix[i][j] == 0) {
            row[i] = col[j] = 1;
          }
        }
      }

      for (size_t i = 0; i < m; i++) {
        if (row[i])
          fill(&matrix[i][0], &matrix[i][n], 0);
      }

      for (size_t j = 0; j < n; j++) {
        if (col[j]) {
          for (size_t i = 0; i < m; i++)  {
            matrix[i][j] = 0;
          }
        }
      }
    }
};

Space Complexity: O(1)

class Solution {
public:
void setZeroes(vector<vector<int> > &matrix) {
    int Col0HasZero = 0, Row0HasZero = 0, NumOfRows = matrix.size(), NumOfCols = matrix[0].size();

    for (int j = 0; j < NumOfCols; j++) {
      if (matrix[0][j] == 0)
        Row0HasZero = 1;
    }
    for (int i = 0; i < NumOfRows; i++) {
        if (matrix[i][0] == 0) 
          Col0HasZero = 1;
        for (int j = 1; j < NumOfCols; j++)
            if (matrix[i][j] == 0)
                matrix[i][0] = matrix[0][j] = 0;
    }
    for (int i = NumOfRows - 1; i >= 0; i--) {
        for (int j = NumOfCols - 1; j >= 1; j--)
            if (matrix[i][0] == 0 || matrix[0][j] == 0)
                matrix[i][j] = 0;
        if (Col0HasZero) 
          matrix[i][0] = 0;
    }
    for (int j = 0; j < NumOfCols; j++) {
      if (Row0HasZero)
        matrix[0][j] = 0;
    }

}
};

上述代码还可继续简化形式：

class Solution {
public:
void setZeroes(vector<vector<int> > &matrix) {
    int Col0HasZero = 0, NumOfRows = matrix.size(), NumOfCols = matrix[0].size();

    for (int i = 0; i < NumOfRows; i++) {
        if (matrix[i][0] == 0) 
          Col0HasZero = 1;
        for (int j = 1; j < NumOfCols; j++)
            if (matrix[i][j] == 0)
                matrix[i][0] = matrix[0][j] = 0;
    }

    for (int i = NumOfRows - 1; i >= 0; i--) {
        for (int j = NumOfCols - 1; j >= 1; j--)
            if (matrix[i][0] == 0 || matrix[0][j] == 0)
                matrix[i][j] = 0;
        if (Col0HasZero) 
          matrix[i][0] = 0;
    }
}
};