Two-dimensional transport process after changing speed interpolation（“Striky air” above the mantle）.

clear all;clf;
% Set parameters
output_interval = 1;
Nt = 80;
Nx_node = 51; 
Ny_node = 51; 
Nloopx = ceil(log2(Nx_node));
Nloopy = ceil(log2(Ny_node));
Lx = 500; 
Ly = 600;
g_y = 10;
% Density :unit(Kg/m^3)
den_plume = 3200;
radius = 100;
den_mantle = 3300;
den_sticky_air = 1;
x_mid = Lx/2;
y_mid = (Ly/2)+50;
x_e_step = Lx / (Nx_node-1);
y_e_step = Ly / (Ny_node-1);
x_enode = 0:x_e_step:Lx;
y_enode = 0:y_e_step:Ly;
num_per_cell = 4;
Nx_marker = (Nx_node-1)*num_per_cell;
Ny_marker = (Ny_node-1)*num_per_cell;
x_m_step = x_e_step./num_per_cell;
y_m_step = y_e_step./num_per_cell;
x_marker = x_m_step./2:x_m_step:Lx - x_m_step./2;
y_marker = y_m_step./2:y_m_step:Ly - y_m_step./2;
[X,Y] = meshgrid( x_m_step/2:x_m_step:Lx - x_m_step/2 , y_m_step/2:y_m_step:Ly - y_m_step/2 );
% The staggered nodes were not complished.
Vx = meshgrid(0:x_e_step:Lx+x_e_step , -x_e_step/2:x_e_step:Lx+x_e_step/2);
Vy = meshgrid(-y_e_step/2:y_e_step:Ly+y_e_step/2 , 0:y_e_step:Ly+y_e_step);
average_vx = zeros(Ny_node+1,Nx_node+1);
average_vy = zeros(Ny_node+1,Nx_node+1);
% Random displacement
for j = 1:Nx_marker
    for i = 1:Ny_marker
    % Random number range from negative 1.25 to positive 1.25
        random_number_x = rand() * x_m_step./4 - x_m_step./8;
        X(i,j) = X(i,j) + random_number_x;
        random_number_y = rand() * y_m_step./4 - y_m_step./8;
        Y(i,j) = Y(i,j) + random_number_y;
    end
end

% Grids has Ny+1 rows and Nx+1 columns
[x,y] = meshgrid(0:x_e_step:Lx,0:y_e_step:Ly);
% Unknown_number is (Ny+1)*(Nx+1)*3
unknown_number = (Nx_node+1)*(Ny_node+1)*3;
coe = sparse(unknown_number,unknown_number);
R = zeros(unknown_number, 1);

% Boundary condition : free slip = -1 ; no slip = 1
bc_left   = -1;
bc_right  = -1;
bc_top    = -1;
bc_bottom = -1;

vis_marker = zeros(Ny_marker,Nx_marker);
den_marker = zeros(Ny_marker,Nx_marker);
x_node = zeros(Ny_marker,Nx_marker);
y_node = zeros(Ny_marker,Nx_marker);
% Plume(3200) and mantle(3300) geometry
for j = 1:Nx_marker
    for i = 1:Ny_marker
        circle = ((j-1)*x_m_step-x_mid).^2+((i-1)*y_m_step-y_mid).^2;
        if circle <= radius.^2
            den_marker(i,j) = den_plume;
            vis_marker(i,j) = 10.^20;%unit:(Pa*s)
        elseif (i-1)*y_m_step <= 100
            den_marker(i,j) = den_sticky_air;
            vis_marker(i,j) = 10.^17;%unit:(Pa*s)
        else
            den_marker(i,j) = den_mantle;
            vis_marker(i,j) = 10.^21;%unit:(Pa*s)
        end
    end
end
w_m_x_node = zeros(Ny_node,Nx_node);
den_w_m = zeros(Ny_node,Nx_node);
vis_w_m = zeros(Ny_node,Nx_node);
node_var_vis_n = zeros(Ny_node+1,Nx_node+1);
node_var_vis_s = zeros(Ny_node,Nx_node);
node_density = zeros(Ny_node,Nx_node);
in_node = zeros(Ny_node+1,Nx_node+1);
in_vx = zeros(Ny_node+1,Nx_node+1);
in_vy = zeros(Ny_node+1,Nx_node+1);
in_p = zeros(Ny_node+1,Nx_node+1);
vx_matrix = zeros(Ny_node+1,Nx_node+1);
vy_matrix = zeros(Ny_node+1,Nx_node+1);
p_matrix = zeros(Ny_node+1,Nx_node+1);
vx_markers = zeros(Ny_marker,Nx_marker);
vy_markers = zeros(Ny_marker,Nx_marker);
%%
% Provides a fixed upper-left node for the interpolation
% of velocity components from nodes to markers.
for j = 1:Nx_marker
    for i = 1:Ny_marker
        L_x = 1;
        R_x = Nx_node;
        for cycle =1:Nloopx
            M_x = fix( (L_x+R_x)./2 );
            if x_enode(M_x) > X(i,j)
                R_x = M_x;
            elseif x_enode(M_x) < X(i,j)
                L_x = M_x;
            end
        end
        x_node(i,j) = L_x;
        L_y = 1;
        R_y = Ny_node;
        for cycle =1:Nloopy
            M_y = fix( (L_y+R_y)./2 );
            if y_enode(M_y) > Y(i,j)
                R_y = M_y;
            elseif y_enode(M_y) < Y(i,j)
                L_y = M_y;
            end
        end
        y_node(i,j) = L_y;
    end
end
x_node1 = x_node;
y_node1 = y_node;

%%
%  Process of 2D transport
figure(1);

for t = 1:3                                                                  
    % Bisection algorithm
    % Searching the coordinate of upper-left node of every L-marker.
    for j = 1:Nx_marker
        for i = 1:Ny_marker
            L_x = 1;
            R_x = Nx_node;
            for cycle =1:Nloopx
                M_x = fix( (L_x+R_x)./2 );
                if x_enode(M_x) > X(i,j)
                    R_x = M_x;
                elseif x_enode(M_x) < X(i,j)
                    L_x = M_x;
                end
            end        
            x_node(i,j) = L_x;    
            L_y = 1;
            R_y = Ny_node;
            for cycle =1:Nloopy
                M_y = fix( (L_y+R_y)./2 );
                if y_enode(M_y) > Y(i,j)
                    R_y = M_y;
                elseif y_enode(M_y) < Y(i,j)
                    L_y = M_y;
                end
            end
            y_node(i,j) = L_y;
        end
    end
  

    % Interpolation from markers to nodes.
    for j = 1:Nx_marker
        for i = 1:Ny_marker
            % Below is also OK
            %dis_x = (x_marker(j)./x_e_step + 1 - x_node(j,1))*x_e_step;
            dis_x = X(i,j) - (x_node(i,j)-1)*x_e_step;
            if(dis_x < x_e_step/2)
                x_node(i,j) = x_node(i,j);
                dis_x = dis_x;
            else
                x_node(i,j) = x_node(i,j)+ 1;
                dis_x = x_e_step - dis_x;
            end
            %dis_y = (y_marker(i)./y_e_step + 1 - y_node(i,1))*y_e_step;
            dis_y = Y(i,j) - (y_node(i,j)-1)*y_e_step;
            if(dis_y < y_e_step/2)
                y_node(i,j) = y_node(i,j);
                dis_y = dis_y;
            else
                y_node(i,j) = y_node(i,j)+ 1;
                dis_y = y_e_step - dis_y;
            end
            % Each marker that carries the original density distribution 
            % is interpolated to the new node after moving, so the index
            % can still be used on the original density distribution.
            w_m_x_node(y_node(i,j),x_node(i,j)) = w_m_x_node(y_node(i,j),x_node(i,j)) + (1 - dis_x./x_e_step).*(1 - dis_y./y_e_step);
            den_w_m(y_node(i,j),x_node(i,j)) = den_w_m(y_node(i,j),x_node(i,j)) + den_marker(i,j).*(1 - dis_x./x_e_step).*(1 - dis_y./y_e_step);
            vis_w_m(y_node(i,j),x_node(i,j)) = vis_w_m(y_node(i,j),x_node(i,j)) + vis_marker(i,j).*(1 - dis_x./x_e_step).*(1 - dis_y./y_e_step);
        end
    end
    % Computing the value of density and viscosity of E-nodes. 
    for j = 1:Nx_node
        for i = 1:Ny_node
            node_density(i,j) = den_w_m(i,j)./w_m_x_node(i,j);
            node_var_vis_s(i,j) = vis_w_m(i,j)./w_m_x_node(i,j);
        end
    end
    % Computing the harmonic density.
    for j = 2:Nx_node
        for i = 2:Ny_node
            % Range of var_vis_n is 2:Ny 2:Nx.
            node_var_vis_n(i,j) = 4./( 1/node_var_vis_s(i,j)+1/node_var_vis_s(i-1,j)...
                    +1/node_var_vis_s(i,j-1)+1/node_var_vis_s(i-1,j-1) );
        end
    end
    % Computing the value of minimal viscosity in the model.
    Kcont = 2*min(min(node_var_vis_n(2:Ny_node,2:Nx_node)))./(x_e_step+y_e_step);

    %% 
    % Solve the 2D-Possion equation.
    
    % The solution of the velocity field is only related to 
    % the distribution of viscosity and density of the E-nodes.
    
    % Set index:that can enhance the velocity of computing.
    for i = 1:Ny_node+1
        for j = 1:Nx_node+1
            in_node(i,j) = (j-1)*(Ny_node+1)+i;
            in_vx(i,j) = 3*in_node(i,j)-2;
            in_vy(i,j) = 3*in_node(i,j)-1;
            in_p(i,j) = 3*in_node(i,j);
        end
    end
    % Set coefficients and right hand side matrix.
    for i = 1:Ny_node+1
        for j = 1:Nx_node+1
            % Condition of Vx
            if(i==1 || i==Ny_node+1 || j==1 || j==Nx_node || j==Nx_node+1)
                % Boundary condition
                coe(in_vx(i,j),in_vx(i,j)) = 1;% vx(i,j) = 0
                % Right hand side
                R(in_vx(i,j),1) = 0;
                % Top free slip
                if(i==1 && j>1 && j<Nx_node) % vx(i,j)-vx(i+1,j) = 0
                    coe(in_vx(i,j),in_vx(i+1,j)) = bc_top; 
                end
                % Bottom free slip
                if(i==Ny_node+1 && j>1 && j<Nx_node)% vx(i,j)-vx(i-1,j) = 0
                    coe(in_vx(i,j),in_vx(i-1,j)) = bc_bottom; 
                end
            % X-Stokes equation    
            else
                coe(in_vx(i,j),in_vx(i,j)) = -2*node_var_vis_n(i,j+1)/(x_e_step.^2)-...
                    2*node_var_vis_n(i,j)/(x_e_step.^2)-node_var_vis_s(i,j)/(y_e_step.^2)...
                    -node_var_vis_s(i-1,j)/(y_e_step.^2);%vx3
                coe(in_vx(i,j),in_vx(i,j-1)) = 2*node_var_vis_n(i,j)./(x_e_step.^2);%vx1
                coe(in_vx(i,j),in_vx(i,j+1)) = 2*node_var_vis_n(i,j+1)./(x_e_step.^2);%vx5
                coe(in_vx(i,j),in_vx(i-1,j)) = node_var_vis_s(i-1,j)./(y_e_step.^2);%vx2
                coe(in_vx(i,j),in_vx(i+1,j)) = node_var_vis_s(i,j)./(y_e_step.^2);%vx4

                coe(in_vx(i,j),in_vy(i-1,j)) = node_var_vis_s(i-1,j)./(x_e_step*y_e_step);%vy1
                coe(in_vx(i,j),in_vy(i,j)) = -node_var_vis_s(i,j)./(x_e_step*y_e_step);%vy2
                coe(in_vx(i,j),in_vy(i-1,j+1)) = -node_var_vis_s(i-1,j)./(x_e_step*y_e_step);%vy3
                coe(in_vx(i,j),in_vy(i,j+1)) = node_var_vis_s(i,j)./(x_e_step*y_e_step);%vy4

                coe(in_vx(i,j),in_p(i,j+1)) = -Kcont./x_e_step;%P2'
                coe(in_vx(i,j),in_p(i,j)) = Kcont./x_e_step;%P1'
                % Right hand side    
                R(in_vx(i,j),1)=0;    
            end
            % Condition of Vy
            if(j==1 || j==Nx_node+1 || i==1 || i==Ny_node || i==Ny_node+1)
                % Boundary condition
                coe(in_vy(i,j),in_vy(i,j)) = 1;% vy(i,j) = 0
                % Right hand side
                R(in_vy(i,j),1) = 0;
                % Left free slip
                if(j==1 && i>1 && i<Ny_node) % vy(i,j)-vy(i,j+1) = 0
                    coe(in_vy(i,j),in_vy(i,j+1)) = bc_left; 
                end
                % Right free slip
                if(j==Nx_node+1 && i>1 && i<Ny_node)% vy(i,j)-vy(i,j-1) = 0
                    coe(in_vy(i,j),in_vy(i,j-1)) = bc_right; 
                end
            % Y-Stokes equation    
            else
                coe(in_vy(i,j),in_vy(i,j)) = -2*node_var_vis_n(i+1,j)/(y_e_step.^2)...
                    -2*node_var_vis_n(i,j)/(y_e_step.^2)-node_var_vis_s(i,j)/(x_e_step.^2)...
                    -node_var_vis_s(i,j-1)/(x_e_step.^2);%vy3
                coe(in_vy(i,j),in_vy(i,j-1)) = node_var_vis_s(i,j-1)./(x_e_step.^2);%vy1
                coe(in_vy(i,j),in_vy(i,j+1)) = node_var_vis_s(i,j)./(x_e_step.^2);%vy5
                coe(in_vy(i,j),in_vy(i-1,j)) = 2*node_var_vis_n(i,j)./(y_e_step.^2);%vy2
                coe(in_vy(i,j),in_vy(i+1,j)) = 2*node_var_vis_n(i+1,j)./(y_e_step.^2);%vy4

                coe(in_vy(i,j),in_vx(i,j-1)) = node_var_vis_s(i,j-1)./(x_e_step*y_e_step);%vx1
                coe(in_vy(i,j),in_vx(i+1,j-1)) = -node_var_vis_s(i,j-1)./(x_e_step*y_e_step);%vx2
                coe(in_vy(i,j),in_vx(i,j)) = -node_var_vis_s(i,j)./(x_e_step*y_e_step);%vx3
                coe(in_vy(i,j),in_vx(i+1,j)) = node_var_vis_s(i,j)./(x_e_step*y_e_step);%vx4

                coe(in_vy(i,j),in_p(i+1,j)) = -Kcont./y_e_step;%P2'
                coe(in_vy(i,j),in_p(i,j)) = Kcont./y_e_step;%P1'
                % Right hand side    
                R(in_vy(i,j),1) = -g_y.*( node_density(i,j-1)+node_density(i,j) )./2;     
            end
            % Condition of P
            if(i==1 || j==1 || i==Ny_node+1 || j==Nx_node+1 || (i==2 && j==2))        
                % Boundary Condition
                coe(in_p(i,j),in_p(i,j))=1; %p(i,j) = 0 
                % Right hand side
                R(in_p(i,j),1)=0; 
                if(i==2 && j==2)
                    coe(in_p(i,j),in_p(i,j))=1*Kcont;% p(2,2) = 0,p=p'*Kcont
                    R(in_p(i,j),1)=0; 
                end
            % Continuity equation    
            else
                coe(in_p(i,j),in_vx(i,j-1)) = -Kcont./x_e_step;%vx1
                coe(in_p(i,j),in_vx(i,j))   =  Kcont./x_e_step;%vx2
                coe(in_p(i,j),in_vy(i-1,j)) = -Kcont./y_e_step;%vy1
                coe(in_p(i,j),in_vy(i,j))   =  Kcont./y_e_step;%vy2
                % Right hand side
                R(in_p(i,j),1)=0;
            end
        end
    end
    % Computing the solution U:include vx,vy and p
    U = coe \ R;

    % Decompose the solution of global matrix.
    for j = 1:Nx_node+1
        for i = 1:Ny_node+1
            vx_matrix(i,j) = U(in_vx(i,j),1);
            vy_matrix(i,j) = U(in_vy(i,j),1);
            p_matrix(i,j) = U(in_p(i,j),1)*Kcont;
        end
    end
    
    % Computing average velocity components at cell centres.
    for j = 1:Nx_node+1
        for i = 1:Ny_node+1
            if (i~=1 && j ~=1)
                average_vx(i,j) = ( vx_matrix(i,j)+vx_matrix(i-1,j)+vx_matrix(i,j-1)+vx_matrix(i-1,j-1) )./4;           
                average_vy(i,j) = ( vy_matrix(i,j)+vy_matrix(i-1,j)+vy_matrix(i,j-1)+vy_matrix(i-1,j-1) )./4;           
            end
        end
    end
    % Applying Free slip condition in the average velocity.
    for j = 1:Nx_node+1
        for i = 1:Ny_node+1
            if (i ==1)
                % x-axis(orthogonal to the y-axis) :vy = 0,vx = vx
                average_vy(i,j) = 0;
                if(j>1 && j<Nx_node+1)
                    average_vx(i,j) = average_vx(i+1,j);
                end
            elseif (j==1)
                % y-axis(orthogonal to the x-axis) :vx = 0,vy = vy
                average_vx(i,j) = 0;
                if(i>1 && i< Ny_node+1)
                    average_vy(i,j) = average_vy(i,j+1);
                end
            end
        end
    end
    %%   
    % Interpolate vx and vy components from E-nodes to L-markers.
    for j = 1:Nx_marker
        for i = 1:Ny_marker
            % Computing dis_x and dis_y.
            % Below note is also OK
            %dis_x = (x_marker(j)./x_e_step + 1 - x_node(j,1))*x_e_step;
            %dis_y = (y_marker(i)./y_e_step + 1 - y_node(i,1))*y_e_step;
            dis_x = X(i,j) - (x_node(i,j)-1)*x_e_step;
            dis_y = Y(i,j) - (y_node(i,j)-1)*y_e_step; 
            % Interpolation from E-nodes to L-markers
            disxm = dis_x./x_e_step;
            disym = dis_y./y_e_step;
            vx_inter1 = (2/3)* vx_matrix(x_node1(i,j),y_node1(i,j))+(1/3)*...
                average_vx(x_node1(i,j),y_node1(i,j));
            vx_inter2 = (2/3)* vx_matrix(x_node1(i,j)+1,y_node1(i,j))+(1/3)*...
                average_vx(x_node1(i,j)+1,y_node1(i,j));
            vx_inter3 = (2/3)* vx_matrix(x_node1(i,j),y_node1(i,j)+1)+(1/3)*...
                average_vx(x_node1(i,j),y_node1(i,j)+1);
            vx_inter4 = (2/3)* vx_matrix(x_node1(i,j)+1,y_node1(i,j)+1)+(1/3)*...
                average_vx(x_node1(i,j)+1,y_node1(i,j)+1);
            vy_inter1 = (2/3)* vy_matrix(x_node1(i,j),y_node1(i,j))+(1/3)*...
                average_vy(x_node1(i,j),y_node1(i,j));
            vy_inter2 = (2/3)* vy_matrix(x_node1(i,j)+1,y_node1(i,j))+(1/3)*...
                average_vy(x_node1(i,j)+1,y_node1(i,j));
            vy_inter3 = (2/3)* vy_matrix(x_node1(i,j),y_node1(i,j)+1)+(1/3)*...
                average_vy(x_node1(i,j),y_node1(i,j)+1);
            vy_inter4 = (2/3)* vy_matrix(x_node1(i,j)+1,y_node1(i,j)+1)+(1/3)*...
                average_vy(x_node1(i,j)+1,y_node1(i,j)+1);
            
            vx_markers(i,j) = vx_inter1*(1-disxm)*...
                (1-disym)+vx_inter2*disxm*(1-disym)...
                +vx_inter3*disym*(1-disxm)+...
                vx_inter4*disxm*disym;                  
            vy_markers(i,j) = vy_inter1*(1-disxm)*...
                (1-disym)+vy_inter2*disxm*(1-disym)...
                +vy_inter3*disym*(1-disxm)+...
                vy_inter4*disxm*disym;                  
        end
    end
    %%  
    % Markers transport from instant t to next t.
    for j = 1:Nx_marker
        for i = 1:Ny_marker
            t_e_step_x = x_e_step./4./( max(max(vx_markers)) );
            t_e_step_y = y_e_step./4./( max(max(vy_markers)) );
            X(i,j) = X(i,j) + vx_markers(i,j)*t_e_step_x;
            Y(i,j) = Y(i,j) + vy_markers(i,j)*t_e_step_y;
            if (X(i,j) > Lx)
                X(i,j) = X(i,j) - Lx;
            elseif(X(i,j) < 0)
                X(i,j) = X(i,j) + Lx;
            end
            if (Y(i,j) > Ly)
                Y(i,j) = Y(i,j) - Ly;
            elseif(Y(i,j) < 0)
                Y(i,j) = Y(i,j) + Ly;
            end
        end
    end
    % Show the process of density's transport.
    if mod(t, output_interval) == 0
%         pcolor(x,y,node_density);
        pcolor(x,y,node_var_vis_s);
        hold on;
        scale = 1;
        quiver(x,y,vx_matrix(1:Ny_node,1:Nx_node),vy_matrix(1:Ny_node,1:Nx_node),scale,color = 'w');
        xlabel('Horizontal(Km)')
        ylabel('Vertical(Km)')
        title(['Node-density after ',num2str(t-1),' deltat'])
        set(gca,'xaxislocation','top');
        set (gca,'YDir','reverse')
        colormap('JET');  
        colorbar;
        shading interp;
        pause(0.01);
    end
end

 

 

 

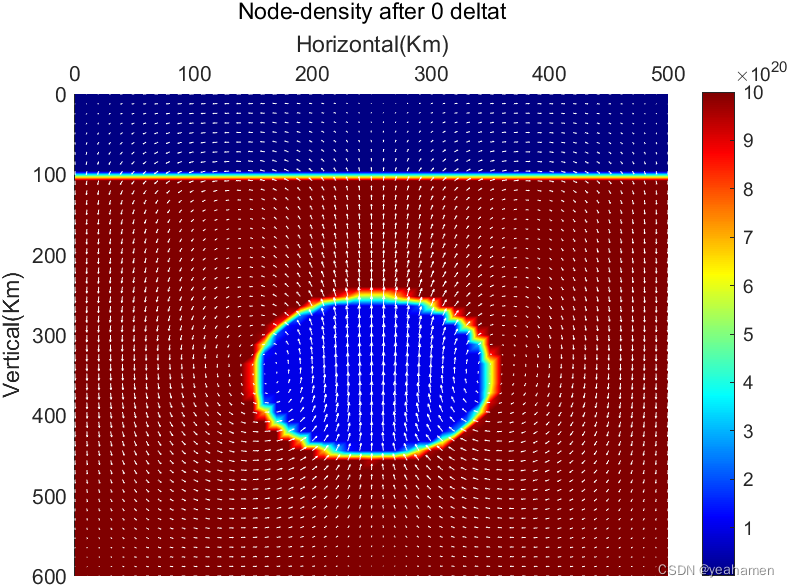
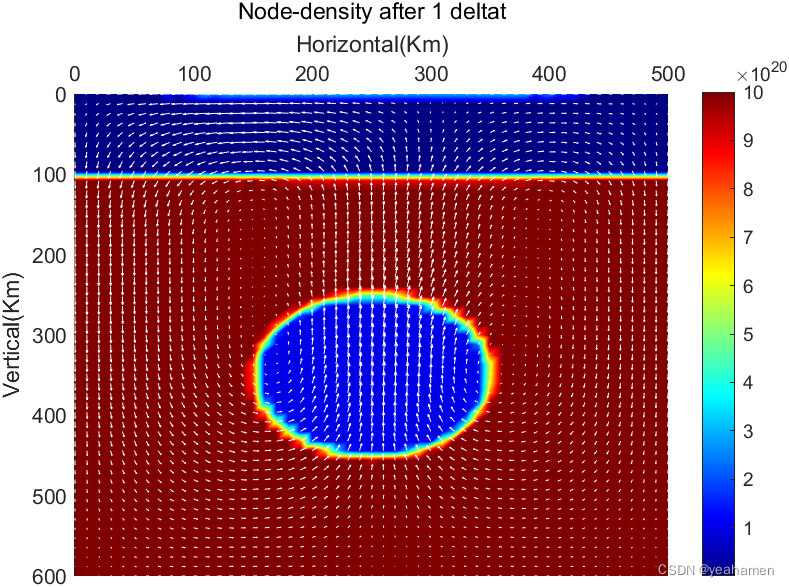
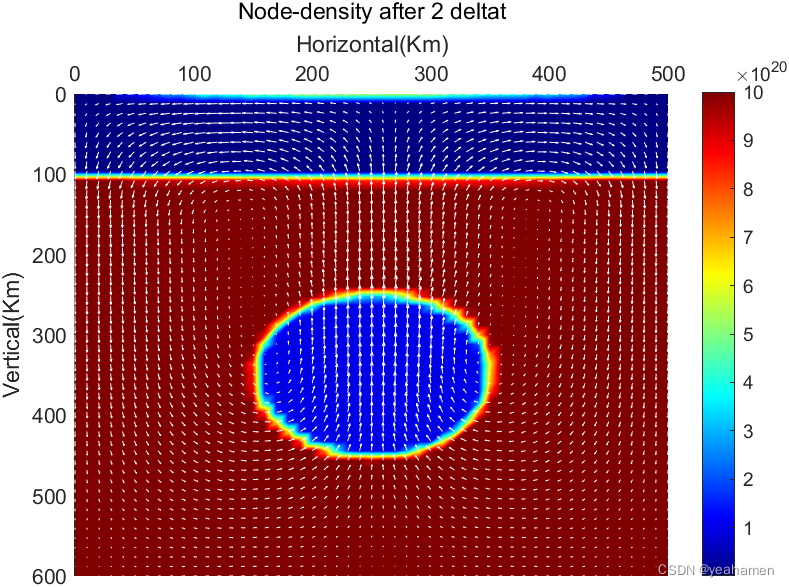
 Change node-density to node-viscosity.