什么是栈
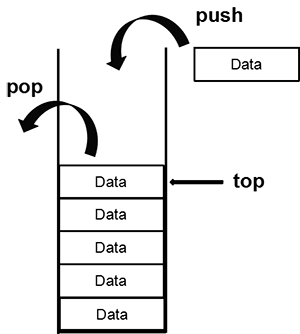
栈是一种特殊的表。我们可以把栈形象地想象成一个木桶:你可以往木桶里存放物品,也可以从木桶里拿取物品。但是每次你只能对木桶顶部的物品进行操作,而无法直接操作木桶底部的物品,除非你把位于其上的所有物品全部取出。
栈的作用
栈的用处很大,下面列举几个主要的应用场合:
1.保存函数调用的参数值;
2.符号匹配([ ], { }, ( ));
3.后缀、中缀表达式的解析。
总之,栈在底层的编译器设计中扮演着及其重要的角色。
栈的实现
一般来说,栈有两种实现方式:链表和数组。链表的优势在于可以动态分配内存;数组的优势则在于速度快,但是需要实现分配固定大小的一块内存。由于一般情况下栈的大小不会太大,而且基本上可以预测出一个最大上限,所以用数组来实现更为常见。笔者实现了一个栈基于数组的栈模板类,支持了绝大部分栈操作。
栈的定义:
template<class T>
class Stack
{
public:
Stack();
~Stack();
bool isEmpty();
bool isFull();
int size();
void create(int maxSize);
void clear();
void destroy();
void push(T val);
void pop();
T peek();
T peekAndPop();
private:
T *array;//用于保存数据的数组
int capacity;//栈当前保存数据的个数
int top;//栈的顶部索引
};下面是具体的栈操作实现:
1.判断栈是否为空
template<class T>
bool Stack<T>::isEmpty()
{
return top == -1;
}2.判断栈是否已满
template<class T>
bool Stack<T>::isFull()
{
return top == capacity - 1;
}3.获取当前栈的大小
template<class T>
int Stack<T>::size()
{
return top + 1;
}4.创建栈
template<class T>
void Stack<T>::create(int maxSize)
{
capacity = maxSize;
array = new T[maxSize];
}5.清空栈
template<class T>
void Stack<T>::clear()
{
top = -1;
}6.删除栈
template<class T>
void Stack<T>::destroy()
{
delete [] array;
top = -1;
}7.压栈
template<class T>
void Stack<T>::push(T val)
{
if (!isFull())
{
array[++top] = val;
}
}8.出栈
template<class T>
void Stack<T>::pop()
{
if (!isEmpty())
{
top--;
}
}9.获取栈顶的数据
template<class T>
T Stack<T>::peek()
{
if (!isEmpty())
{
return array[top];
}
return NULL;
}10.获取栈顶的数据并将其出栈
template<class T>
T Stack<T>::peekAndPop()
{
if (!isEmpty())
{
return array[top--];
}
return NULL;
}栈的应用实例:中缀表达式的计算
中缀表达式指的是形如“100 + 37 - 22 * (7 -4) / 4”结构的表达式。表达式包含数字和操作符两中字符,中间用空格隔开。这种表达式比较符合人的阅读模式,但是程序却很难直接理解其中的逻辑。因此,我们需要对中缀表达式进行一些处理,具体步骤如下:
1.符号匹配检测。符号匹配检测指的是对[ ], { }, ( )等相对出现的符号进行匹配检测,这里检测的是( 和 )的匹配;
2.将中缀表达式转换成后缀表达式。后缀表达式也叫“逆波兰”(reverse Polish)记法。举个例子,后缀表达式“3 4 * 5 +”转化成中缀表达式为“3 * 4 + 5”,这里要做的正好是该转换的逆过程;
3. 计算后缀表达式的值。
值得一提的是,这三个步骤都用到了栈,可见栈用处之广泛。
1.符号匹配检测
char leftSymbols[] = {'(', '{', '[', '\'', '\"'};
char rightSymbols[] = {')', '}', ']', '\'', '\"'};
//sentence为需要被检测的表达式,leftSymbols和rightSymbols分别为左右匹配的字符,symbolNum为匹配字符的个数
bool SymbolMatcher::matchTest(const char *sentence, const char leftSymbols[], const char rightSymbols[], int symbolNum)//匹配
{
int len = strlen(sentence);
stack->create(len);
for (int i=0; i<len; i++)
{
char c = sentence[i];
if (find(leftSymbols, leftSymbols + symbolNum, c) != leftSymbols + symbolNum)//如果该字符是一个左匹配字符,直接压栈
{
stack->push(c);
}
else if (find(rightSymbols, rightSymbols + symbolNum, c) != rightSymbols + symbolNum)//如果该字符是一个右匹配字符
{
if (stack->isEmpty())//如果为空栈,说明匹配失败
{
return false;
}
else//否则,判断栈顶的字符是不是和该右匹配字符匹配的左匹配字符
{
char topc = stack->peekAndPop();
if (find(leftSymbols, leftSymbols + symbolNum, topc) - leftSymbols != find(rightSymbols, rightSymbols + symbolNum, c) - rightSymbols)
{
return false;
}
}
}
}
return true;
}2.将中缀表达式转换成后缀表达式
首先实现一个c++ string的split函数
void split(string s, string delim, vector<string> &ret)
{
size_t last = 0;
size_t index = s.find_first_of(delim, last);
while (index != string::npos)
{
ret.push_back(s.substr(last, index - last));
last = index+1;
index = s.find_first_of(delim, last);
}
if (index - last > 0)
{
ret.push_back(s.substr(last, index - last));
}
}然后将中缀表达式转换成后缀表达式
void InfixCalculator::infixToPostfix(const char *sentence, string &str)
{
vector<string> splits;
split(sentence, " ", splits);//分割字符串
int num = splits.size();
stack->create(num);//创建栈
for (size_t i=0; i<num; i++)//遍历分割的字符串序列
{
string s = splits[i];
string tops;
if (s == "+" || s == "-")
{
while(!stack->isEmpty())
{
tops = stack->peek();
if(tops == "+" || tops == "-" || tops == "*" || tops == "/")
{
stack->pop();
str.append(tops + " ");
}
else
{
break;
}
}
stack->push(s);
}
else if (s == "*" || s == "/")
{
while(!stack->isEmpty())
{
tops = stack->peek();
if(tops == "*" || tops == "/")
{
stack->pop();
str.append(tops + " ");
}
else
{
break;
}
}
stack->push(s);
}
else if (s == "(")
{
stack->push(s);
}
else if (s == ")")
{
while(!stack->isEmpty())
{
tops = stack->peek();
if (tops != "(")
{
stack->pop();
str.append(tops + " ");
}
else
{
break;
}
}
stack->pop();
}
else
{
str.append(s + " ");
}
}
while(!stack->isEmpty())
{
str.append(stack->peekAndPop() + " ");
}
str = str.substr(0, str.size() - 1);
}3.计算后缀表达式的值
bool PostfixCalculator::calc(const char *sentence, double &ret)
{
vector<string> splits;
split(sentence, " ", splits);//分割字符串
int num = splits.size();
stack->create(num);//创建栈
for (int i=0; i<num; i++)//遍历分割的字符串序列
{
//具体规则是:1.如果遇到数字就压栈 2.如果遇到操作符就把栈顶的两个元素出栈并进行运算,然后将运算结果压栈
string s = splits[i];
if (s == "+")
{
if (stack->size() < 2)
{
return false;
}
double b = stack->peekAndPop();
double a = stack->peekAndPop();
double sum = a + b;
stack->push(sum);
}
else if (s == "-")
{
if (stack->size() < 2)
{
return false;
}
double b = stack->peekAndPop();
double a = stack->peekAndPop();
double difference = a - b;
stack->push(difference);
}
else if (s == "*")
{
if (stack->size() < 2)
{
return false;
}
double b = stack->peekAndPop();
double a = stack->peekAndPop();
double product = a * b;
stack->push(product);
}
else if (s == "/")
{
if (stack->size() < 2)
{
return false;
}
double b = stack->peekAndPop();
double a = stack->peekAndPop();
if (b == 0.0)
{
return false;
}
double quotient = a / b;
stack->push(quotient);
}
else
{
double d = atof(s.c_str());
stack->push(d);
}
}
if (stack->size() != 1)
{
return false;
}
ret = stack->peekAndPop();
return true;
}结果展示
测试程序
#include "infixcalculator.h"
using namespace std;
int main()
{
InfixCalculator infixCalculator;
double ret;
if(!infixCalculator.calc("10 / 6 * 8 + ( 3 * 4 - 7 ) / 5", ret))
{
cout << "Expression is invalid!" << endl;
}
else
{
cout << ret << endl;
}
if(!infixCalculator.calc("10 / 6 * 8 + ( ( 3 * 4 - 7 ) / 5", ret))
{
cout << "Expression is invalid!" << endl;
}
else
{
cout << ret << endl;
}
return 0;
}运行结果








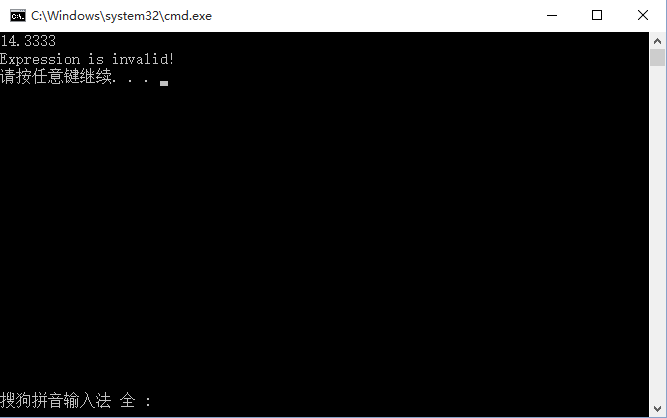
















 2766
2766

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








