算法设计中经常会用到递归,利用递归式的方法可以清晰地显示算法的整个过程,而对于分析算法的复杂度,解递归式就有了用处,这里的方法来自于《算法导论》。
(一)代换法(substitution method):
实质上就是数学归纳法,先对一个小的值做假设,然后推测更大的值得正确性。由于是数学归纳法,那么我们就需要对值进行猜测。现在,我们看下面这个例子:

我们先假设一个结论T(n) = O(lg(n - b)),并且假设对T(n / 2上取整)成立(这就是数学归纳法了),那么把T(n / 2上取整)用假设的结论进行代换,我们有T(n) <= lg((n - b)) / 2上取整)
<= lg((n - b) / 2 + 1) + 1 = lg(n - b + 2),对于任意的b >= 2,即满足要求T(n) <= lg(n) = O(lgn)。证毕。
这是一个很简单的例子,但是其中有些事情还是要交代的。
一个是结论的猜测不是一个容易的事情。另一个是在上面的例子中我没有直接下结论说T(n) = O(lg(n)),而是减去了一个常数b,这是为什么呢?答案是:we can prove something stronger for a given value by assuming something stronger for smaller values.还有一点值得说明,请看下面这个例子:

这里出现了sqrt(n),我们采用变量代换的方法:令n = 2 ^ m,则上式变为T(2 ^ m) = 2T(2 ^ (m / 2) ),再设S(m) = T(2 ^ m),则得到S(m) = 2S(m / 2) + 1。我们先假设S(m) = m - b <= O(m),且对S(m / 2)成立,那么S(m) = 2 * (m - b) / 2 + 1 = m - b + 1,对于任意的b >= 1都有S(m) = O(m),然后回代有T(n) = T( 2 ^ m) = S(m) = O(m) = O(lgn)。
这里我们采用了变量代换的方法。如果假设时,感觉变量不明朗,那么这是一种很有效的方法。
(二)递归树方法(recursion tree):
递归树最适合猜出合适的结果,然后用代换法验证
利用递归树方法求算法复杂度我想最好的例子就是归并排序了,这里我不想拿归并排序做例子,而只是用书中一些更简单形象的例子来说明:

根据上式我们建立递归式T(n) = 3T(n / 4) + cn^2,这里我们抛去上下界函数的影响(sloppiness that we can tolerate),并且把Theta(n ^ 2)用cn^2代替。下面建立递归树模型:




在递归树中,每一个结点都代表一个子代价,每层的代价是该层所有子代价的总和,总问题的代价就是所有层的代价总和。
所以,我们利用递归树求解代价,需要知道什么呢,一个是每一层的代价,一个是层数,就是这两个。
这些,都需要我们用觉察的态度来发现,而事实证明,这不是一件难事,很多情况下是有规律可循的。
我们且看上面这个例子,递归树的构造很简单,当递归调用到边界是,就达到了常量T(1),达到常量T(1)所用到的递归次数就是整个递归树的深度,我们从图中可以得到第i层的结点的代价为n / ( 4 ^ i ),当n / (4 ^ i) = 1即i = log4(n)时,递归到达了边界,所以,整个递归树的深度就是i = log4(n)。我们要求的总的代价是所有的总和,结果为O(n ^ 2)。计算过程我就不再累述了。但是,递归树并不是都是这样的满的树,也就是不是每一层的结点都是相同的结构,所以我们在构造递归树的时候要仔细看好这一点,才能保证在计算时不会出错。
当叶子不全在一个高度上时,我们可以先忽略这个误差,认为全是在最底层,然后用代换法验证是否成立。
(三)主方法(master method):
The master theorem concerns recurrence relations of the form:
In the application to the analysis of a recursive algorithm, the constants and function take on the following significance:
- n is the size of the problem.
- a is the number of subproblems in the recursion.
- n/b is the size of each subproblem. (Here it is assumed that all subproblems are essentially the same size.)
- f (n) is the cost of the work done outside the recursive calls, which includes the cost of dividing the problem and the cost of merging the solutions to the subproblems.
It is possible to determine an asymptotic tight bound in these three cases:
Case 1
Generic form
If  where
where  (using Big O notation)
(using Big O notation)
then:
Example
As one can see from the formula above:
-
 , so
, so
-
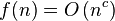 , where
, where

Next, we see if we satisfy the case 1 condition:
-
 .
.
It follows from the first case of the master theorem that
(indeed, the exact solution of the recurrence relation is 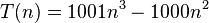 , assuming
, assuming  ).
).
Case 2
Generic form
If it is true, for some constant k ≥ 0, that:
-
 where
where

then:
Example

As we can see in the formula above the variables get the following values:
-

-
 where
where

Next, we see if we satisfy the case 2 condition:
-
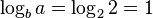 , and therefore, yes,
, and therefore, yes,

So it follows from the second case of the master theorem:
Thus the given recurrence relation T(n) was in Θ(n log n).
(This result is confirmed by the exact solution of the recurrence relation, which is 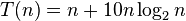 , assuming
, assuming  .)
.)
Case 3
Generic form
If it is true that:
-
 where
where

and if it is also true that:
-
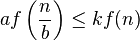 for some constant
for some constant
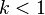 and sufficiently large
and sufficiently large
 (often called the
regularity condition)
(often called the
regularity condition)
then:
Example[edit]
As we can see in the formula above the variables get the following values:
-

-
 , where
, where

Next, we see if we satisfy the case 3 condition:
-
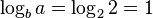 , and therefore, yes,
, and therefore, yes,

The regularity condition also holds:
-
 , choosing
, choosing

So it follows from the third case of the master theorem:
Thus the given recurrence relation T(n) was in Θ(n2), that complies with the f (n) of the original formula.
(This result is confirmed by the exact solution of the recurrence relation, which is  , assuming
, assuming  .)
.)
Inadmissible equations
The following equations cannot be solved using the master theorem:
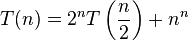
- a is not a constant; the number of subproblems should be fixed
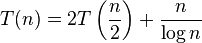
-
non-polynomial difference between f(n) and
 (see below)
(see below)
-
non-polynomial difference between f(n) and

- a<1 cannot have less than one sub problem

- f(n) which is the combination time is not positive

- case 3 but regularity violation.
In the second inadmissible example above, the difference between  and
and  can be expressed with the ratio
can be expressed with the ratio 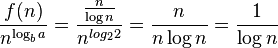 . It is clear that
. It is clear that 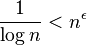 for any constant
for any constant  . Therefore, the difference is not polynomial and the Master Theorem does not apply.
. Therefore, the difference is not polynomial and the Master Theorem does not apply.








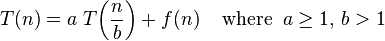
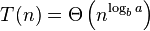



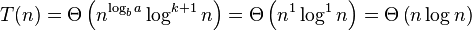

















 6134
6134

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








