马尔可夫不等式 Markov's inequality

最新推荐文章于 2024-05-27 18:48:47 发布

andyyang0212

最新推荐文章于 2024-05-27 18:48:47 发布

阅读量8.9k

点赞数 3

分类专栏：数学文章标签：概率论数学

本文链接：https://blog.csdn.net/andyyang0212/article/details/39270489

版权

数学专栏收录该内容

1 篇文章 0 订阅

订阅专栏

If X is any nonnegative integrable random variable and a > 0, then

$\mathbb{P}(X \geq a) \leq \frac{\mathbb{E}(X)}{a}.$
$\mu(\{x\in X:|f(x)|\geq \varepsilon \}) \leq {1\over \varepsilon}\int_X |f|\,d\mu.$

In the language of measure theory, Markov's inequality states that if (X, Σ, μ) is a measure space, ƒ is a measurable extended real-valued function, and $\varepsilon>0$ , then

证明

For any event E, let I_E be the indicator random variable of E, that is, I_E = 1 if E occurs and I_E = 0 otherwise.

Using this notation, we have I_(X ≥ a) = 1 if the event X ≥ a occurs, and I_(X ≥ a) = 0 if X < a. Then, given a > 0,

aI_{(X \geq a)} \leq X\,

which is clear if we consider the two possible values of I_(X ≥ a). If X < a, then I_(X ≥ a) = 0, and so aI_(X ≥ a) = 0 ≤ X. Otherwise, we have X ≥ a, for which I_(X ≥ a) = 1 and so aI_(X ≥ a) = a ≤ X.

Since 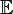$\mathbb{E}$ is a monotonically increasing function, taking expectation of both sides of an inequality cannot reverse it. Therefore

\mathbb{E}(aI_{(X \geq a)}) \leq \mathbb{E}(X).\,

Now, using linearity of expectations, the left side of this inequality is the same as

a\mathbb{E}(I_{(X \geq a)}) = a(1\cdot\mathbb{P}(X \geq a) + 0\cdot\mathbb{P}(X < a)) = a\mathbb{P}(X \geq a).\,

Thus we have

a\mathbb{P}(X \geq a) \leq \mathbb{E}(X)\,

and since a > 0, we can divide both sides by a.

andyyang0212

关注

3
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
马尔可夫不等式 Markov's inequality

If X is any nonnegative integrable random variable and a > 0, thenIn the language of measure theory, Markov's inequality states that if (X, Σ, μ) is a measure space, ƒ is a measurable
复制链接

扫一扫

专栏目录