java实现左式堆

最新推荐文章于 2024-07-07 15:32:59 发布

anlian523

最新推荐文章于 2024-07-07 15:32:59 发布

阅读量476

点赞数

分类专栏：数据结构与算法

本文链接：https://blog.csdn.net/anlian523/article/details/78115886

版权

数据结构与算法专栏收录该内容

30 篇文章 16 订阅

订阅专栏

任一节点X的零路径长（null path length）npl（X）定义为到从X到一个不具有两个儿子的节点的最短路径的长。

不具有两个儿子的节点即是叶子节点和单孩子节点。

所以叶子节点和单孩子节点的npl都是0，因为自身到自身的距离为0.

规定空节点即null，则npl（null）为-1.此规定也为以下定理服务。

定理：任一节点的零路径长比它的两个儿子的零路径长的最小值大1，所以说叶子节点和单孩子节点的零路径长为0，因为这两种节点都有一个孩子是空节点，即儿子中npl最小值为-1，根据定理，这两种节点的npl=-1+1=0.

左式堆的性质：对于堆中的每一个节点X，左儿子的零路径长是大于等于右儿子的零路径长。

代码如下，注释帮助理解：

// LeftistHeap class
//
// CONSTRUCTION: with a negative infinity sentinel
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x )       --> Insert x
// Comparable deleteMin( )--> Return and remove smallest item
// Comparable findMin( )  --> Return smallest item
// boolean isEmpty( )     --> Return true if empty; else false
// void makeEmpty( )      --> Remove all items
// void merge( rhs )      --> Absorb rhs into this heap
// ******************ERRORS********************************
// Throws UnderflowException as appropriate

/**
 * Implements a leftist heap.
 * Note that all "matching" is based on the compareTo method.
 * @author Mark Allen Weiss
 */
public class LeftistHeap<AnyType extends Comparable<? super AnyType>>
{
    /**
     * Construct the leftist heap.
     */
    public LeftistHeap( )
    {
        root = null;//构造函数，根为空
    }

    /**
     * Merge rhs into the priority queue.
     * rhs becomes empty. rhs must be different from this.
     * @param rhs the other leftist heap.
     */
    public void merge( LeftistHeap<AnyType> rhs )
    {
        if( this == rhs )    // Avoid aliasing problems如果是同样的两个堆
            return;

        root = merge( root, rhs.root );//重载进入参数为两个节点的函数。为俩个根节点
        rhs.root = null;//此时传进来的rhs已经被合并，直接引用置空
    }

    /**
     * Internal method to merge two roots.
     * Deals with deviant cases and calls recursive merge1.
     */
    private LeftistNode<AnyType> merge( LeftistNode<AnyType> h1, LeftistNode<AnyType> h2 )
    {
        if( h1 == null )//如果是第一次进入则是排除掉某个堆为空的情况
            return h2;  //如果不是第一次，那就可能是递归过程的终点之一
        if( h2 == null )
            return h1;  //递归终点之一
        if( h1.element.compareTo( h2.element ) < 0 )//将两个根进行比较，小的根为第一个参数，大的为第二个参数
            return merge1( h1, h2 );//进入到实际的合并函数中
        else
            return merge1( h2, h1 );
    }

    /**
     * Internal method to merge two roots.
     * Assumes trees are not empty, and h1's root contains smallest item.
     */
    private LeftistNode<AnyType> merge1( LeftistNode<AnyType> h1, LeftistNode<AnyType> h2 )
    {
        if( h1.left == null )   // Single node如果左子树为空，那么根据左式堆的性质，肯定是个单节点
            h1.left = h2;       // Other fields in h1 already accurate h2已经满足左式堆了，递归终点之一
            //这个终点，其实就是，h1是小的根，肯定是把h2往h1上放，而h1.left == null其实就是h1为单节点，而这是
            //merge1函数的唯一特殊情况
        else
        {
            h1.right = merge( h1.right, h2 );
            if( h1.left.npl < h1.right.npl ) //合并后如果左比右的零路径长小
                swapChildren( h1 );
            h1.npl = h1.right.npl + 1;//因为性质，节点的零路径长的等于两儿子节点的零路径长的最小值加1，而
            //而左儿子的零路径长是>=右儿子的零路径长的，所以直接按右儿子的零路径长加1就好
        }
        return h1;
    }

    /**
     * Swaps t's two children.
     */
    private static <AnyType> void swapChildren( LeftistNode<AnyType> t )
    {   //交换左右子树
        LeftistNode<AnyType> tmp = t.left;
        t.left = t.right;
        t.right = tmp;
    }

    /**
     * Insert into the priority queue, maintaining heap order.
     * @param x the item to insert.
     */
    public void insert( AnyType x )
    {//插入单节点就是特殊的合并，直接调用真实的merge函数
        root = merge( new LeftistNode<>( x ), root );//参数顺序并不重要，因为merge函数会进行比较的
    }

    /**
     * Find the smallest item in the priority queue.
     * @return the smallest item, or throw UnderflowException if empty.
     */
    public AnyType findMin( )
    {
        if( isEmpty( ) )
            throw new UnderflowException( );
        return root.element;
    }

    /**
     * Remove the smallest item from the priority queue.
     * @return the smallest item, or throw UnderflowException if empty.
     */
    public AnyType deleteMin( )
    {
        if( isEmpty( ) )
            throw new UnderflowException( );
        //删除就是删除根，再合并左右子树
        AnyType minItem = root.element;
        root = merge( root.left, root.right );

        return minItem;
    }

    /**
     * Test if the priority queue is logically empty.
     * @return true if empty, false otherwise.
     */
    public boolean isEmpty( )
    {
        return root == null;
    }
    /**
     * Make the priority queue logically empty.
     */
    public void makeEmpty( )
    {
        root = null;
    }

    private static class LeftistNode<AnyType>
    {
            // Constructors
        LeftistNode( AnyType theElement )
        {
            this( theElement, null, null );
        }

        LeftistNode( AnyType theElement, LeftistNode<AnyType> lt, LeftistNode<AnyType> rt )
        {
            element = theElement;
            left    = lt;
            right   = rt;
            npl     = 0;
        }

        AnyType              element;      // The data in the node
        LeftistNode<AnyType> left;         // Left child
        LeftistNode<AnyType> right;        // Right child
        int                  npl;          // null path length
    }
    
    private LeftistNode<AnyType> root;    // root

    public static void main( String [ ] args )
    {
        int numItems = 100;
        LeftistHeap<Integer> h  = new LeftistHeap<>( );
        LeftistHeap<Integer> h1 = new LeftistHeap<>( );
        int i = 37;

        for( i = 37; i != 0; i = ( i + 37 ) % numItems )
            if( i % 2 == 0 )
                h1.insert( i );
            else
                h.insert( i );
        
        h.merge( h1 );//合并，最终你会发现堆里的数为1-99，这些数
        for( i = 1; i < numItems; i++ )
            if( h.deleteMin( ) == i )
                System.out.println( "Oops! " + i );//你会发现根为1，删除掉根后，根为2，以此类推
    }
}

左式堆最重要的操作就是合并，是一个递归过程，此操作的普通情况是将H1 H2(H1的根节点比H2的小)，将H1的右子堆与H2合并，将合并后的新堆，再作为H1的右子堆。而其他情况都是特殊情况，在注释已经说明，是递归终点。

在说一下主函数的for循环，看似很奇怪，循环出现的数字是99个看似乱序的数字，实际上观察后你会发现：

1.这些肯定是1-99的这99个数字的乱序。

2.第一次出现的数和最后一次的数加起来等于100，第二次和倒数第二次的数也是，以此类推。

其实可以这么理解：

数字以37的步伐开始填充1-99这99个位置（因为每次循环后就会37+37），第一次填充的数就是第一次循环的数，想象位置首尾相连，最终会把这些位置都填充完。

为什么出现的数没有0和100呢，是因为：0根本不可能，因为都是一直在加的，而加的数都是正数。100出现时是循环的终点，在最后一次循环，System.out.println(i)，即输出了最后一个i值，然后执行i = ( i + 37 ) % numItems，而这里i+37加起来肯定等于100，因为是终点。所以最后输出的数肯定100-37即63.

如果你把循环里的37都改成别的数，分两种情况：

1.如果别的数不能被100整除，那么出现的数就是99个，即某种顺序的1-99

2.如果别的数能被100整除，那么出现的数的个数就是，（100/改的数）-1。道理很简单，因为能被整除，所以不会填充过程从尾跳到首的情况。

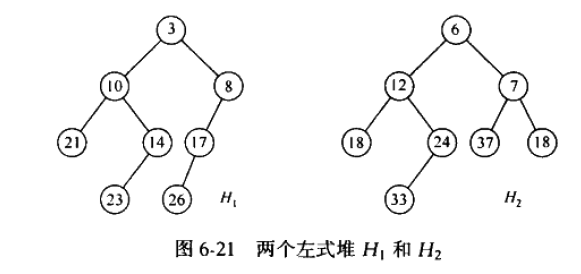
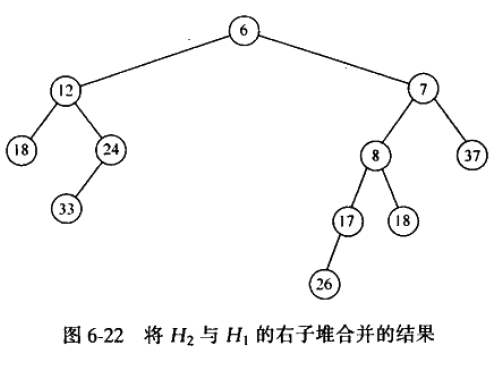
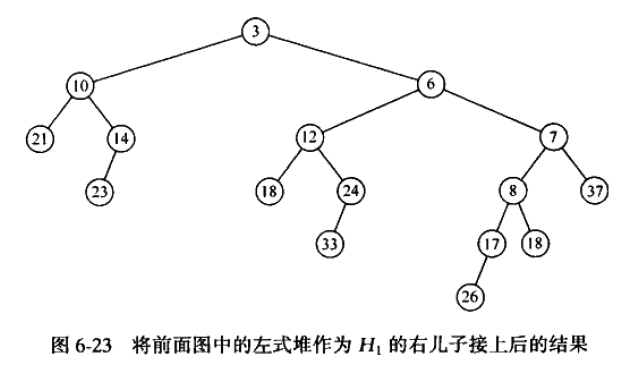
下面贴一下合并的图解过程：