机器学习（一）——线性回归、分类与逻辑回归

http://antkillerfarm.github.io/

序

这是根据Andrew Ng的《机器学习讲义》，编写的系列blog。

http://www.cnblogs.com/jerrylead/archive/2012/05/08/2489725.html

这是网友jerrylead翻译整理的版本，也是本文的一个重要的参考。

http://www.tcse.cn/~xulijie/

这是jerrylead的个人主页。

我写的版本在jerrylead版本的基础上，略有增删，添加了一下其他资料里的内容。

还有就是使用Mathjax书写公式，便于其他人的修改与传播。

线性回归

线性回归属于有监督学习（supervised learning）的其中一种方法。

对于一个给定的训练集（training set）$(x,y)$，其中$y=h(x)=h(x_1,x_2,\dots,x_n)$，在$h$未知的情况下，求得$h$或者$h$的近似解的过程，被称为猜测（hypothesis）。hypothesis的目的是，能在给定$x$的情况下，预测$y$。

如果$y$是连续函数，那么这个过程叫做回归（regression）问题。如果$y$是离散函数，那么这个过程叫做分类（classification）问题。

$$h_{\theta}(x)=\theta_0+\theta_1x_1+\dots+\theta_nx_n=\sum_{i=0}^n\theta_ix_i=\theta^Tx \tag{1}$$

满足公式1条件的回归问题，被称作线性回归（Linear Regression）。

为了评估公式1中待定系数$\theta$的预测准确度，我们定义如下代价函数（cost function）：

$$J(\theta)=\frac{1}{2}\sum_{i=0}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 \tag{2}$$

其中，m表示训练集的个数（从0算起），$x^{(i)}$表示第i个训练样本。

代价函数的表达式，实际上就是正态分布的方差计算公式，它体现了拟合后的函数曲线与样本集之间的偏差程度。显然，代价函数的值越小，预测准确度越高。

Jacobian矩阵

Jacobian矩阵是矩阵A的一阶导数矩阵，定义如下：

$$J(A)=\frac{\mathrm{d}f}{\mathrm{d}x}= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}$$

注：Carl Gustav Jacob Jacobi，1804～1851，德国数学家，柏林大学博士。

当$m=1$时，该矩阵又被称为梯度向量：

$$\nabla(A)=\begin{bmatrix} \frac{\partial f}{\partial x_1} & \cdots & \frac{\partial f}{\partial x_n} \\ \end{bmatrix}$$

Hessian矩阵

Hessian矩阵是矩阵A的二阶导数矩阵，定义如下：

$$H(A)= \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\partial x_n} \\ \frac{\partial^2 f}{\partial x_2\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n\partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\ \end{bmatrix}$$

注：Ludwig Otto Hesse，1811～1874，德国数学家，毕业于柯尼斯堡大学，Jacobi的学生。

因为$\frac{\partial^2 f}{\partial x_i\partial x_j}=\frac{\partial^2 f}{\partial x_j\partial x_i}$(克莱罗定理，Clairaut’s theorem)，所以Hessian矩阵通常是一个对称矩阵。

参考：

http://blog.csdn.net/dsbatigol/article/details/12558891

梯度下降算法

公式2的求极值问题，实际上就是求驻点（stationary point）的问题，即求$\nabla(f)=0$的点的问题。

梯度下降（gradient descent）算法的原理，从直观来说，就是沿着梯度向量的反方向，向坡底前进。该算法是一个递归算法，其迭代公式为：

$$x_{k+1}=x_k-t_kA_k\nabla f(x_k)$$

其中，$t_k$表示迭代的步长，$\nabla f(x_k)$为梯度向量，$A_k$为系数矩阵。根据$t_k$和$A_k$的取法不同会产生出各种各样的变种算法。

例如，当$A_k=H(x_k)^{-1}$时，就是著名的牛顿迭代法（Newton Method）。可以证明，牛顿迭代法具有二阶收敛性（在二阶以内的所有系数矩阵中，收敛最快）。

名称	梯度下降算法	牛顿迭代法
迭代次数	收敛慢，迭代次数多。	收敛快，迭代次数少。
迭代计算复杂度	$O(n)$	$O(n^3)$
实现难点	步长需要一定的方法来确定。	$H(x_k)$需要满秩，且$H(x_k)^{-1}$的计算比较复杂，尤其是维数很高的时候。

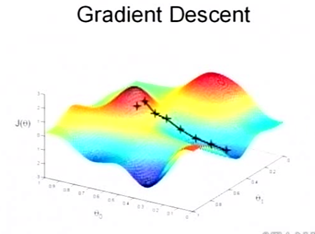
梯度下降算法只有当函数为凸函数时，才会严格收敛到最小值。否则的话，可能只是极小值，而非最小值。如下图所示：

凸集（Convex set）的图例如下所示：

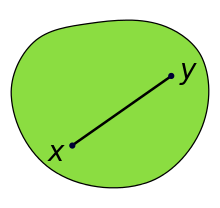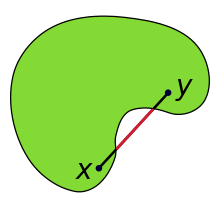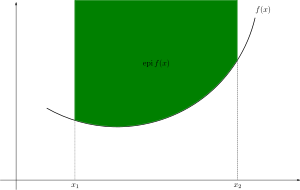Convex set	non-Convex set	convex function

参考：

http://freemind.pluskid.org/machine-learning/gradient-descent-wolfe-s-condition-and-logistic-regression/

http://freemind.pluskid.org/machine-learning/newton-method/

LMS算法

LMS（least mean squares，最小均方）算法，也是一种迭代算法。其迭代公式为：

$$\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta_j} \tag{3}$$

其中，$:=$表示赋值操作，$J(\theta)$是公式2所示的代价函数，$\alpha$被称作学习率（learning rate）。

可以看出，LMS的迭代公式是梯度下降算法的一个特例，其中，$\alpha$相当于步长，系数矩阵$A=E$，这里的$E$表示单位矩阵。

将公式2代入公式3，可得：

$$\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j \tag{4}$$

迭代方式分为两种：

1.批量梯度下降（batch gradient descent）算法。方法如下：

Repeat until convergence {
$\theta_j:=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j$(for every j)
}

2.随机梯度下降（stochastic gradient descent）算法。方法如下：

Loop {
for i=1 to m, {
$\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j$(for every j)
}
}

名称 | 批量梯度下降 | 随机梯度下降
|:–:|:–:|:–:|
特点 | 每向前走一步，都需要遍历整个训练样本集。 | 一个样本接着一个样本的处理数据。
计算复杂度 | 大 | 小
收敛程度 | 收敛 | 由于新样本引入新的误差，该算法只能收敛到一定程度，而不能无限逼近最小值。

正规方程组算法

正规方程组（Normal Equations）算法，是传统的以解方程的方式求最小值的方法。

如果，令

$$X=\begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \vdots \\ (x^{(m)})^T \end{bmatrix}, \vec{y}=\begin{bmatrix} (y^{(1)}) \\ (y^{(2)}) \\ \vdots \\ (y^{(m)}) \end{bmatrix}$$

则：

$$\theta=(X^TX)^{-1}X^T\vec{y}$$

这种解方程的算法，实际上就是通常所说的最小二乘法（Least squares）。

优点：解是精确解，而不是近似解。不是迭代算法，程序实现简单。不在意$X$特征的scale。比如，特征向量$X=\{x_1, x_2\}$, 其中$x_1$的range为1~2000，而$x_2$的range为1~4，可以看到它们的范围相差了500倍。如果使用梯度下降方法的话，会导致椭圆变得很窄很长，而出现梯度下降困难，甚至无法下降梯度（因为导数乘上步长后可能会冲到椭圆的外面）的问题。

缺点：维数高的时候，矩阵求逆运算的计算量很大。

插值问题

回归问题在数学上和插值问题是同一类问题。除了线性插值（回归）之外，还有多项式插值（回归）问题。

这里以一元函数为例，描述一下多项式插值问题。

对于给定的$k+1$$个点$$(x_0,y_0),\dots,(x_k,y_k)$，求$f(x)=\sum_{i=0}^ka_ix^i$经过给定的$k+1$个点。显然$k=1$的时候，是线性插值。

多项式插值算法有很多种，最经典是以下两种：

1.拉格朗日插值算法（the interpolation polynomial in the Lagrange form）

$$L(x)=\sum_{j=0}^ky_jl_j(x),l_j(x)=\prod_{0\le m\le k\atop m\neq j}\frac{x-x_m}{x_j-x_m}$$

2.牛顿插值算法（the interpolation polynomial in the Newton form）

$$N(x)=\sum_{j=0}^ka_jn_j(x),n_j(x)=\prod_{i=0}^{j-1}(x-x_i),a_j=[y_0,\dots,y_j]$$

此外还有分段插值法，即将整个定义域分为若干区间，在区间内部进行线性插值或多项式插值。

欠拟合与过拟合

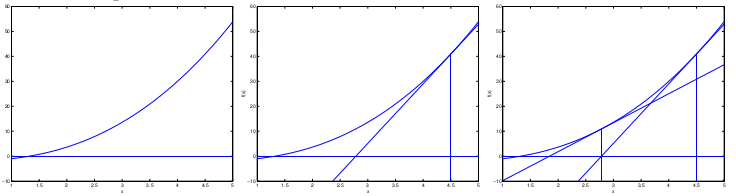
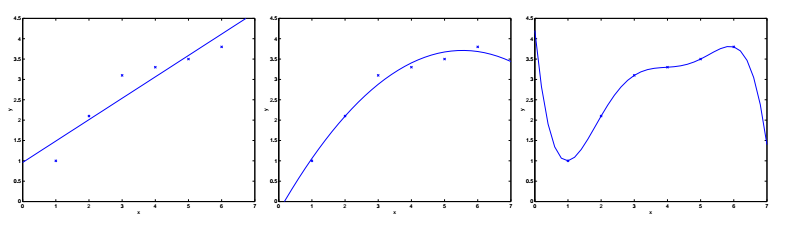
对于上图所示的6个采样点，采用线性回归时（左图），拟合程度不佳。如果采用二次曲线（中图）的话，效果就要好得多了。但也不是越多越好，比如五次曲线（右图）的情况下，虽然曲线完美的经过了6个采样点，但却偏离了实际情况——假设横轴表示房屋面积，纵轴表示房屋售价。

我们把左图的情况叫做欠拟合（Underfitting），右图的情况叫做过拟合（Overfitting）。

这里换个角度看：如果我们把上述多项式回归中的$x,x^2,\dots,x^n$看作是线性回归时的特征集的话，那么多项式回归就可以转化成为线性回归。

从中可以看出，欠拟合或过拟合实际上就是线性回归中的特征集选取问题。特征集选取不当，就会导致预测不准。

局部加权线性回归

局部加权线性回归（LWR，locally weighted linear regression）算法是一种对特征集选取不敏感的算法。它将公式2中的代价函数修改为：

$$J(\theta)=\frac{1}{2}\sum_{i=0}^m\omega^{(i)}(h_{\theta}(x^{(i)})-y^{(i)})^2 \tag{5}$$

其中，$\omega^{(i)}$被称为权重，它有多种选取方法，最常用的是：

$$\omega^{(i)}=\exp\left(-\frac{(x^{(i)}-x)^2}{2\tau^2}\right)$$

其中，$\tau$被称为带宽（bandwidth）。实际上，这就是一个高斯滤波器。离采样点x越近，其权重越接近1。

分类与逻辑回归

二分类

结果集y的取值只有0和1的分类问题被称为二分类，其中0被称为negative class，1被称为positive class，也可用“-”和“+”来表示。

逻辑回归

为了将线性回归的结果约束到$[0,1]$区间，我们将公式1修改为：

$$h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \tag{6}$$

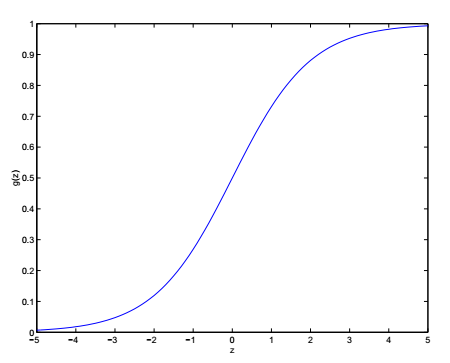
公式6又被称为logistic function或sigmoid function。函数$g(z)$的图像如下所示：

事实上，任何$[0,1]$区间的平滑增函数，都可以作为$g(z)$，但公式6的好处在于

$$g'(z)=\frac{1}{(1+e^{-z})^2}e^{-z}=\frac{1}{(1+e^{-z})}\left(1-\frac{1}{(1+e^{-z})}\right)=g(z)(1-g(z))\tag{7}$$

评估逻辑回归（Logistic regression）的质量，需要用到最大似然估计（maximum likelihood estimator）方法（由Ronald Aylmer Fisher提出）。最大似然估计是在“模型已定，参数未知”的情况下，寻找使模型出现的概率最大的参数集$\theta$的方法。显然，参数集$\theta$所确定的模型，其出现概率越大，模型的准确度越高。

最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的（independent and identically distributed，IID），即：

$$f(x_1,\dots,x_n;\theta)=f(x_1;\theta)\times \dots \times f(x_n;\theta)$$

似然估计函数如下所示：

$$L(\theta)=\prod_{i=1}^mp(y^{(i)}\vert x^{(i)};\theta)$$