蓝桥杯 2017 省 AB包子凑数

P8646 [蓝桥杯 2017 省 AB] 包子凑数

题目描述

小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有 $N$ 种蒸笼，其中第 $i$ 种蒸笼恰好能放 $A_i$ 个包子。每种蒸笼都有非常多笼，可以认为是无限笼。

每当有顾客想买 $X$ 个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有 $X$ 个包子。比如一共有 $3$ 种蒸笼，分别能放 $3$ 、 $4$ 和 $5$ 个包子。当顾客想买 $11$ 个包子时，大叔就会选 $2$ 笼 $3$ 个的再加 $1$ 笼 $5$ 个的（也可能选出 $1$ 笼 $3$ 个的再加 $2$ 笼 $4$ 个的）。

当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有 $3$ 种蒸笼，分别能放 $4$ 、 $5$ 和 $6$ 个包子。而顾客想买 $7$ 个包子时，大叔就凑不出来了。

小明想知道一共有多少种数目是包子大叔凑不出来的。

输入格式

第一行包含一个整数 $N$。$(1\le N\le 100)$。

以下 $N$ 行每行包含一个整数 $A_i$。$(1\le A_i\le 100)$。

输出格式

一个整数代表答案。如果凑不出的数目有无限多个，输出 INF。

输入输出样例 #1

输入 #1

2  
4  
5

输出 #1

6

输入输出样例 #2

输入 #2

2  
4  
6

输出 #2

INF

说明/提示

对于样例 $1$，凑不出的数目包括：$1,2,3,6,7,11$。

对于样例 $2$，所有奇数都凑不出来，所以有无限多个。

蓝桥杯 2017 省赛 A 组 H 题。

--------------------------------------------------------------------------------------

思路

其中 x就是我们要凑的数，A为包子数，K为包子笼数

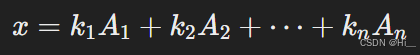
令g为A1,A2…An的最大公约数
上式为

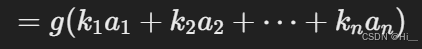
则可以看到x是最大公约数g的倍数，则当g>1时则有无穷多凑不出来的数字

所以
首先判断最大公约数g是否>1
然后动态规划，把所有关于Ai的线性组合求出来

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int mgcd(int n,int m)
{
	while(m)
	{
		int tmp=m;
		m=n%m;
		n=tmp;
	}
	return n;
}

ll n;
ll arr[105];
ll dp[100005]; 
int main(void)
{
	cin>>n;
	for(int i=0;i<n;i++)
	cin>>arr[i];
	
	int g=mgcd(arr[0],arr[1]);
	for(int i=2;i<n;i++)
	{
		g=mgcd(g,arr[i]);
	}
	if(g>1)
	{
		cout<<"INF";
		return 0;
	}
	
	dp[0]=1;
	for(int i=0;i<n;i++)
	{
		for(int j=arr[i];j<100005;j++)
		{
			//若dp[j-arr[i]]能求出来 那么dp[j]通过加上Ai也能求出来
			dp[j]=max(dp[j],dp[j-arr[i]]);
		}
	}
	
	ll ans=0;
	for(int i=0;i<100005;i++)
	{
		if(dp[i]==0)
		{
			ans++;
		}
	}
	cout<<ans;
	return 0;
}