Lucas定理
A、B是非负整数,p是质数。AB写成p进制:A=a[n]a[n-1]...a[0],B=b[n]b[n-1]...b[0]。
则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0]) modp同
即:Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)
以求解n! % p为例,把n分段,每p个一段,每一段求的结果是一样的。但是需要单独处理每一段的末尾p, 2p, ...,把p提取出来,会发现剩下的数正好又是(n / p)!,相当于划归成了一个子问题,这样递归求解即可。这个是单独处理n!的情况,当然C(n,m)就是n!/(m!*(n-m)!),每一个阶乘都用上面的方法处理的话,就是Lucas定理了,注意这儿的p是素数是有必要的。
Lucas最大的数据处理能力是p在10^5左右,不能再大了,hdu 3037就是10^5级别的!
未写main函数
const maxn=100005;
var n,m:int64;
fac:array [0..maxn] of int64;
function quickmod(a,b,mol:int64):int64;
var ans:int64;
begin
ans:=1;
while b<>0 do
begin
if (b and 1)=1 then ans:=(ans*a) mod mol;
a:=a*a mod mol;
b:=b>>1;
end;
exit(ans);
end;
function get_fact(p:int64):int64;
var i:longint;
begin
fac[0]:=1;
for i:=1 to p do
fac[i]:=(fac[i-1]*i) mod p;
end;
function lucas(n,m,p:int64):int64;
var ans,aa,bb:int64;
begin
ans:=1;
while (a>0) and (k>0) do
begin
aa:=a mod p;
bb:=b mod p;
if aa<bb then exit(0);
ans:=ans*fac[aa]*quickmod(fac[bb]*fac[aa-bb] mod p,p-2,p) mod p;
a:=a div p;
k:=k div p;
end;
exit(ans);
end;
当p很大怎么搞?显然这样直接开数组会MLE
我们可以这样做。
分子相乘取模,分母相乘取模
对分母求逆元,分子乘逆元取模
给个代码


const mol=1000000007;
var n,m:longint;
function inv(a,p:int64):int64;
var b,c,q,k1,k2,k3:int64;
begin
b:=p;
c:=a mod b;
q:=a div b;
k1:=1;
k2:=0;
k3:=(k1+p-q*k2 mod p) mod p;
while (c xor 1)<>0 do
begin
a:=b;
b:=c;
c:=a mod b;
q:=a div b;
k1:=k2;
k2:=k3;
k3:=(k1+p-q*k2 mod p) mod p;
end;
exit(k3);
end;
function calc(x,y:int64):int64;
var i,j,ans,up,down:int64;
begin
i:=y+1;
j:=x;
up:=1;
down:=1;
while i<=j do
begin
up:=up*i mod mol;
inc(i);
end;
i:=x-y;
while i>=1 do
begin
down:=down*i mod mol;
dec(i);
end;
ans:=inv(down,mol);
ans:=up*ans mod mol;
exit(ans);
end;
begin
read(n,m);
writeln(calc(n+m,m));
end.
再来说逆元:
对于正整数

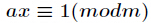
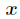


逆元一般用扩展欧几里得算法来求得,如果
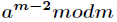
推导过程如下
求现在来看一个逆元最常见问题,求如下表达式的值(已知
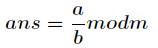
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求

种通用的求逆元方法,适合所有情况。公式如下
现在我们来证明它,已知
接下来来实战一下,看几个关于逆元的题目。(转自ACdreamer犇的blog)
题目:http://poj.org/problem?id=1845
题意:给定两个正整数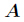
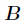

分析:很容易知道,先把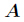
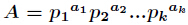
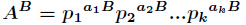
的所有因子和的表达式如下
第二种方法就是用等比数列求和公式,但是要用逆元。用如下公式即可
因为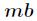
其实有些题需要用到


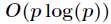
如果对于一个1000000级别的素数
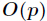
它的推导过程如下,设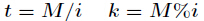
对上式两边同时除
再把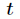
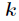
初始化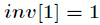


另外


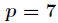
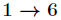
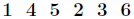
题目:http://www.lydsy.com/JudgeOnline/problem.php?id=2186
题意:求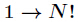
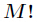
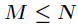
分析:因为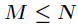
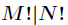
对于两个正整数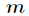
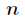
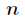
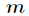
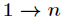
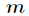
本结论是很好证明的,因为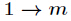
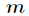
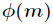
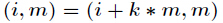
结论成立。那么对于本题,答案就是
其中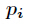
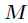
求逆元就有技巧了,用刚刚介绍的递推法预处理,否则会TLE的。
接下来还有一个关于逆元的有意思的题目,描述如下
证明:由
其中
所以只需要证明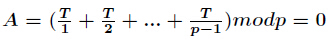
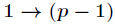

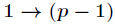
所以进一步得到
证明完毕!







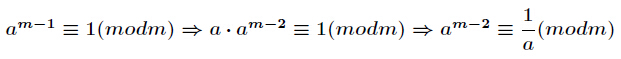
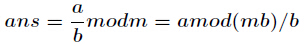
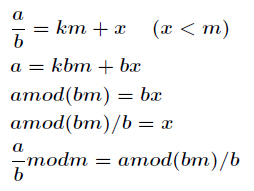
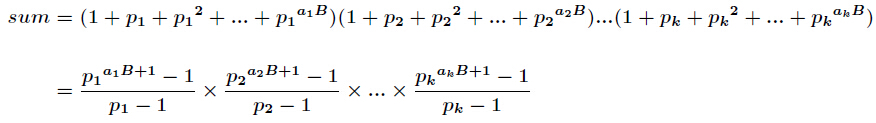
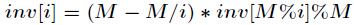
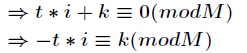
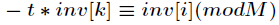
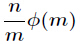
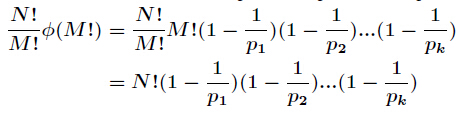

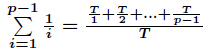
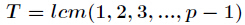
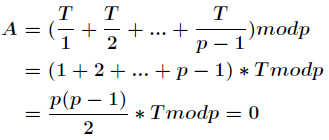














 310
310

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








