KNN分类器-CSDN博客

KNN学习（K-Nearest Neighbor algorithm，K最邻近方法）是一种统计分类器，对数据的特征变量的筛选尤其有效。

基本原理

KNN的基本思想是：输入没有标签（标注数据的类别），即没有经过分类的新数据，首先提取新数据的特征并与測试集中的每一个数据特征进行比較；然后从測试集中提取K个最邻近（最类似）的数据特征标签，统计这K个最邻近数据中出现次数最多的分类，将其作为新的数据类别。
KNN的这样的基本思想有点类似于生活中的“物以类聚。人以群分”。
在KNN学习中，首先计算待分类数据特征与训练数据特征之间的距离并排序。取出距离近期的K个训练数据特征。然后根据这K个相近训练数据特征所属类别来判定新样本类别：假设它们都属于一类，那么新的样本也属于这个类；否则，对每一个候选类别进行评分，依照某种规则确定新的样本的类别。

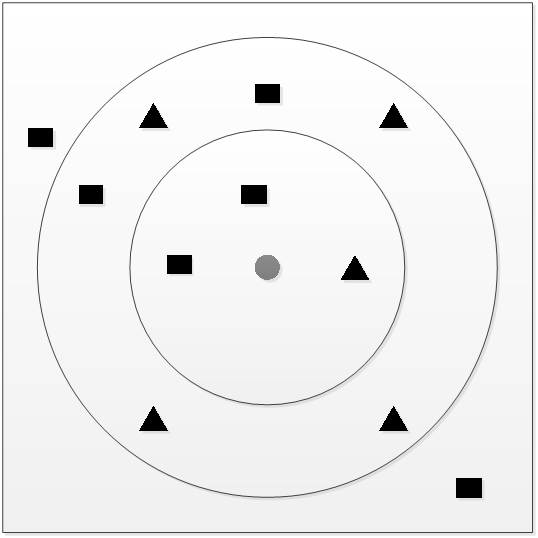
笔者借用以下这个图来做更形象的解释：
这里写图片描写叙述
如上图，图中最小的那个圆圈代表新的待分类数据。三角形和矩形分别代表已知的类型，如今须要推断圆圈属于菱形那一类还是矩形那一类。

可是我该以什么样的根据来推断呢？

看离圆形近期（K=1）的那个类型是什么，由图可知，离圆形近期的是三角形，故将新数据判定为属于三角形这个类别。
看离圆形近期的3个数据（K=3）的类型是什么，由图可知离圆形近期的三个中间有两个是矩形，一个是三角形，故将新数据判定为属于矩形这个类别。
看离圆形近期的9个数据（K=9）的类型是什么，由图可知离圆形近期的9个数据中间，有五个是三角形。四个是矩形。故新数据判定为属于三角形这个类别。

上面所说的三种情况也能够说成是1-近邻方法、3-近邻方法、9-近邻方法。。。当然，K还能够取更大的值，当样本足够多，且样本类别的分布足够好的话，那么K值越大，划分的类别就越正确。而KNN中的K表示的就是划分数据时。所取类似样本的个数。

我们都知道，当K=1时，其抗干扰能力就较差。由于假如样本中出现了某种偶然的类别，那么新的数据非常有可能被分错。为了添加分类的可靠性，能够考察待測数据的K个近期邻样本。统计这K个近邻样本中属于哪一类别的样本最多，就将样本X判属于该类。
当然。假设在样本有限的情况下，KNN算法的误判概率和距离的详细測度方法就有了直接关系。即用何种方式判定哪些数据与新数据近邻。不同的样本选择不同的距离測量函数，这能够提高分类的正确率。通常情况下，KNN能够採用Euclidean（欧几里得）、Manhattan（曼哈顿）、Mahalanobis（马氏距离）等距离用于计算。

Euclidean距离为： $d (x ⃗, y ⃗) = [\sum i = 1 n (x i - y i) 2]$ $x ⃗ = (x 1, x 2, . . ., x n)$ $y ⃗ = (y 1, y 2, . . ., y n)$
Manhattan距离为： $d (x ⃗, y ⃗) = \sum i = 1 n | x i - y i |$
Mahalanobis距离为： $d (x ⃗, y ⃗) = (x ⃗ - y ⃗)' V - 1 (x ⃗ - y ⃗)$ 当中n为特征的维数，V为x⃗ 和y⃗ 所在的数据集的协方差函数。

以下给出KNN学习的伪代码：

Algorithm  KNN(A[n],k,x)
    Input:
        A[n]为N个训练样本的特征，K为近邻数，x为新的样本；
    Initialize:
        取A[1]~A[k]作为x的初始近邻。
        计算測试样本与x间的欧式距离d(x,A[i]),i=1,2...,k;
        按d(x,A[i])升序排序。
        计算最远样本与x间距离D。即max{d(x,A[i])}；
    for(i=k+1;i<=n;i++)
        计算A[i]与x之间的距离d(x,A[i])；
        if （d(x,A[i])）<D  then  用A[i]取代最远样本。
        依照d(x,A[i])升序排序；
        计算最远样本与x间的距离D，即max{d(x,A[i])}；
    End for
    计算前K个样本A[i],i=1,2...,k所属类别的概率。
    具有最大概率的类别即为样本x的类；
    Output:x所属的类别。

KNN的不足

1、添加某些类别的样本容量非常大，而其它类样本容量非常小，即已知的样本数量不均衡。有可能当输入一个和小容量类同样的的新样本时，该样本的K个近邻中，大容量类的样本占多数，从而导致误分类。
针对此种情况能够採用加权的方法，即和该样本距离小的近邻所相应的权值越大，将权值纳入分类的參考根据。
2、分类时须要先计算待分类样本和全体已知样本的距离。才干求得所需的K近邻点，计算量较大，尤其是样本数量较多时。
针对这样的情况能够事先对已知样本点进行剪辑。去除对分类作用不大的样本，这一处理步骤仅适用于样本容量较大的情况，假设在原始样本数量较少时採用这样的处理。反而会添加误分类的概率。

改进的KNN算法

KNN学习easy受噪声影响，尤其是样本中的孤立点对分类或回归处理有非常大的影响。因此通常也对已知样本进行滤波和筛选，去除对分类有干扰的样本。

K值得选取也会影响分类结果。因此需根据每类样本的数目和分散程度选取合理的K值，而且对不同的应用也要考虑K值得选择。

基于组合分类器的KNN改进算法

经常使用的组合分类器方法有投票法、非投票法、动态法和静态法等，比方简单的投票法中全部的基分类器对分类採取同样的权值；权值投票法中每一个基分类器具有相关的动态权重，该权重能够随时间变化。

首先随机选择属性子集。构建多个K近邻分类器；然后对未分类元组进行分类。最后把分类器的分类结果依照投票法进行组合，将得票最多的分类器作为终于组合近邻分类器的输出。

基于核映射的KNN改进算法

将原空间Rn中的样本x映射到一个高维的核空间F中，突出不同类别样本之间的特征差异出。使得样本在核空间中变得线性可分或者近似线性可分，其流程例如以下所看到的：
首先进行非线性映射：

Φ : R n \to F, x \to Φ (x)

然后在高维的核空间。待分类的样本变为

(Φ(x1),...,Φ(xn))。随意两个样本

Φ(xi)。

Φ(xj)之间的距离为：

∥ Φ (x i) - Φ (x j) ∥ 2 = K (x i, x i) + K (x j, x j)

当中

K(∗,∗)为核函数，在此基础上进行KNN分类。

实践代码

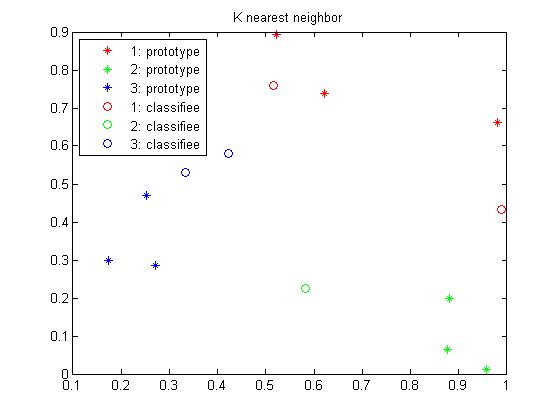
以下给出一个简单的KNN分类的MATLAB实践代码：
main.m文件

function main
trainData = [
    0.6213    0.5226    0.9797    0.9568    0.8801    0.8757    0.1730    0.2714    0.2523
    0.7373    0.8939    0.6614    0.0118    0.1991    0.0648    0.2987    0.2844    0.4692
    ];
trainClass = [
    1     1     1     2     2     2     3     3     3
    ];
testData = [
    0.9883    0.5828    0.4235    0.5155    0.3340
    0.4329    0.2259    0.5798    0.7604    0.5298
    ];

% main
testClass = cvKnn(testData, trainData, trainClass);

% plot prototype vectors
classLabel = unique(trainClass);
nClass     = length(classLabel);
plotLabel = {'r*', 'g*', 'b*'};
figure;
for i=1:nClass
    A = trainData(:, trainClass == classLabel(i));
    plot(A(1,:), A(2,:), plotLabel{i});
    hold on;
end

% plot classifiee vectors
plotLabel = {'ro', 'go', 'bo'};
for i=1:nClass
    A = testData(:, testClass == classLabel(i));
    plot(A(1,:), A(2,:), plotLabel{i});
    hold on;
end
legend('1: prototype','2: prototype', '3: prototype', '1: classifiee', '2: classifiee', '3: classifiee', 'Location', 'NorthWest');
title('K nearest neighbor');
hold off;

KNN.m文件

function [Class, Rank] = cvKnn(X, Proto, ProtoClass, K, distFunc)
if ~exist('K', 'var') || isempty(K)
    K = 1;%默觉得K = 1
end
if ~exist('distFunc', 'var') || isempty(distFunc)
    distFunc = @cvEucdist;
end
if size(X, 1) ~= size(Proto, 1)
    error('Dimensions of classifiee vectors and prototype vectors do not match.');
end
[D, N] = size(X);

% Calculate euclidean distances between classifiees and prototypes
d = distFunc(X, Proto);

if K == 1, % sort distances only if K>1
    [mini, IndexProto] = min(d, [], 2); % 2 == row%每列的最小元素
    Class = ProtoClass(IndexProto);
    if nargout == 2, % instance indices in similarity descending order
        [sorted, ind] = sort(d'); % PxN
        RankIndex = ProtoClass(ind); %,e.g., [2 1 2 3 1 5 4 1 2]'
        % conv into, e.g., [2 1 3 5 4]'
        for n = 1:N
            [ClassLabel, ind] = unique(RankIndex(:,n),'first');
            [sorted, ind] = sort(ind);
            Rank(:,n) = ClassLabel(ind);
        end
    end
else
    [sorted, IndexProto] = sort(d'); % PxN
    clear d。
    % K closest
    IndexProto = IndexProto(1:K,:);
    KnnClass = ProtoClass(IndexProto);
    % Find all class labels
    ClassLabel = unique(ProtoClass);
    nClass = length(ClassLabel);
    for i = 1:nClass
        ClassCounter(i,:) = sum(KnnClass == ClassLabel(i));
    end
    [maxi, winnerLabelIndex] = max(ClassCounter, [], 1); % 1 == col
    % Future Work: Handle ties somehow
    Class = ClassLabel(winnerLabelIndex);
end

Eucdist.m文件

function d = cvEucdist(X, Y)
 if ~exist('Y', 'var') || isempty(Y)
     %% Y = zeros(size(X, 1), 1);
     U = ones(size(X, 1), 1);
     d = abs(X'.^2*U).'; return;
 end
 V = ~isnan(X); X(~V) = 0; % V = ones(D, N); 
 %clear V;
 U = ~isnan(Y); Y(~U) = 0; % U = ones(D, P); 
 %clear U;
 %d = abs(X'.^2*U - 2*X'*Y + V'*Y.^2);
 d1 = X'.^2*U;
 d3 = V'*Y.^2;
 d2 = X'*Y;
 d = abs(d1-2*d2+d3);