先解释下名词的意思。
无向图的割:就是去掉一些边。使得原图不连通。最小割就是要去掉边的数量最小。
解决问题的经常使用办法就是Stoer-Wagner 算法;
先说下这个算法的步骤后面给出证明:
1.min=MAXINT,固定一个顶点P
2.从点P用类似prim的s算法扩展出“最大生成树”,记录最后扩展的顶点和最后扩展的边
3.计算最后扩展到的顶点的分割值(即与此顶点相连的全部边权和),若比min小更新min
4.合并最后扩展的那条边的两个端点为一个顶点
5.转到2,合并N-1次后结束
6.min即为所求,输出min
这个算法过程不难理解,我在这里还是简单的演示下算法的过程,
任选一个点P,開始了扩展之路初始化wage数组的值都是0。而且已把点P放入了已扩展点的集合;
第一个点P扩展完的wage数组的值例如以下图
(图中边上的权值是表示两点间相连的边的条数,也能够觉得是两点间的连通度)
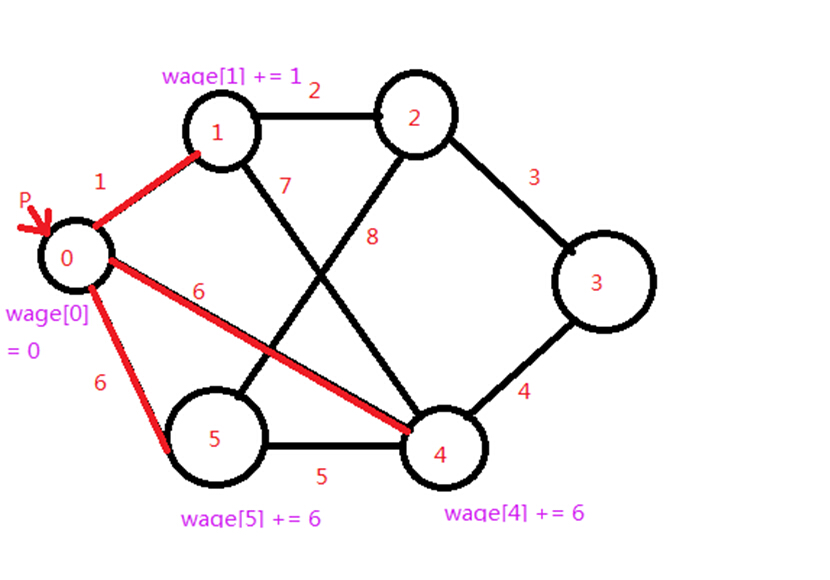
wage[4]的值最大这时候把点4增加到已訪问集合;
下一次就选取wage数组最大值的点(也就是点4)開始向外扩展,注意在扩展点4的时候点P不会再被更新,
由于它已经进入被扩展集合了。过程同上。
重复扩展。。
。
扩展到最后两个点的时候我们记为S,T。
当中T是最后一个点。
这时候我们得到了wage[S] 和 wage[T];
如今有例如以下性质:
1,wage[T]是将单点T分离出原图的最小的割的值(这里说的是把T这个点单独拿出去);
2,wage[T]的值是将S或T单独分离出原图的最小割值中较小的那一个。
首先性质一非常好证明,由于你最后更新到wage[T]的时候 wage[T]的值就是全部与它相连的边的权值的和,显然成立;
性质二的证明分为两种情况,S与T有边相连,和无边相连;
S与T有边相连时,在通过S进行扩展时,因为先选择S所以扩展前wage[S]>=wage[T] 在扩展时 wage[T]的值必定会添加S与T之间的权值。
可是这个权值也是属于S的
两个相加了同一个数,因为之前wage[S]>=wage[T] 所以相加同一个数后不等式仍然成立。
同理S,T无边相连也能够仿照上面的解释;
以下要进行合点操作了,我们须要证明一件事情就是合点操作后不会影响终于的答案,
说明这个问题前,我们先进行以下的一个讨论。
算法进行到这就到了合并点的步骤了,我们先来分析下上面prim算法的过程,
首先对于上面的性质1和性质2你要已经理解了以下的说明你才会认为清晰。
到眼下为止好像对于我们实用处的就是最后那两个点S,T。我们不禁要问下,
假设仅仅是为了选出两个点。有必要这么麻烦吗(最大生成树)?
直接任意选两个点。计算出相应的wage的值,
即计算把他们单独切割出去的值,比較大小。小的记为T大的记为S。然后跟新min。
好像也满足了上面所要的结果。
显然这么做不正确。我们考虑以下一种情况
我们先来想一想切割后的情况,如果我们找到了原图的最小割然后依照最小割集进行切割。
那么原图一定被分为两部分且仅仅能是两部分,记为A,B ;
A,B彼此连同,切割后的A,B 显然是不连通的。
为了简化证明过程我如果 原图A与B 仅有一条边相连。当然这条边的值就是最小割的值。
这条边连接的两个点一个在A中一个在B中 分别记为啊a,b。
假设A中或B中仅仅有一个点,那么你依照任意选点的方法不会影响最后的答案,我们这里要讨论A和B中点的个数大于1。
这时假设你还任意的找两个点进行更新min 合点操作就会出错了。
这非常好想,由于假设你选的是a,b 两个点,
那么你计算出的wage肯定是大于最小割,由于不管a,b都肯定与至少2个点相连。而终于的答案是a,b间边的权值。
这时假设把a,b合点后再进行上面的反复操作显然已经把最佳答案错过了。
所以上面的这选点的prim是为了确定一个顺序问题,我还以这个样例来说,
通过prim选出的两个点S,T一定都在A中或者在B中(前提是A,B中包括2个或以上的点)
也仅仅有在这个前提下进行点的合并才不会影响最后的答案。
我们先来证明下这两个点一定在一边而不会是一边一个(前提是A,B中包括2个或以上的点)
证明:
最好还是设我们prim 过程的第一个点在A中,那么它一定先在A中的点開始扩展操作,
进行prim扩展若干次后首次计算B中点的wage 时
一定是A,B相连的那个点
此时wage[b]的值为最小割的值,接下来。
假设A中可扩展的点的wage值都大于wage[b],
那一定是A中的点都扩展玩了才会去扩展B中的点
那么最后的两个点一定都在B中。
否者,首次由b点開始扩展时候,
我们能够肯定的就是在A中可扩展的点的wage值都小于wage[b],
假设接下来B中的可扩展的点的wage值一直都大于A中可扩展点的wage值
那么就是B中的点全都扩展完然后再进行A中的扩展最后两个点就都在A中。
否则。在B中扩展若干次,再次回到A中扩展的时候,
B中可扩展点的wage值都小于A中的可扩展点的值,
由前面可知这个值一定小于wage[b]。
接下来就是依照这个思路。假设一直在A中那么最后的点在B中,
假设再次回到B中扩展可知此时A中可扩展的点的wage值都小于B中可扩展点的wage值,重复重复下去,
假设最后A中一个点,B中一个点,会出现什么情况呢?显然最后的那个点的wage值小于wage[b]了。
这样更新完原图的最小割更小了。这显然这显然矛盾了。
矛盾的原因就在于prim的过程根本就没法实现一个在A中一个在B中。
有了这么个结论再讨论合点不影响最后答案就非常显然了,略微想一想画一画就懂了这里就不细致说了
假设S,T相连, 我已经更新了将S,T切割单独切割出去时最小割的值。
那么如今即使将S和T合并也不会影响全局最小割的求解。
假设S,T不直接相连时,假设答案是S,T合并后的解显然将两者一起分离的时候已经将T单独分开了。
肯定不会是最优的答案由于画蛇添足啊。所以将S和T合并。并不会影响后面的计算。
到此我就粗略的说完了 无向图最小割的算法的正确性。以及证明。
合点操作之所以不影响答案的关键是prim算法的步骤决定了选点的顺序。
代码例如以下O(n^3)优化的事实上效率并没有提高。
。
这个要依据题目数据决定。
測试题目:厦大OJ 1100。
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define maxn 105
#define inf 1000000
int node[maxn],cnt[maxn],vis[maxn],p[maxn][maxn];
int main()
{
int n,m,a,b,ans=inf;
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++)
{
if(i<n)
node[i]=i;
scanf("%d%d",&a,&b);
p[a][b]++;
p[b][a]++;
}
while(n>1)
{
memset(vis,0,sizeof(vis));
vis[node[0] ] =1;
int maxi = 1;
for(int i=0;i<n;i++)
{
cnt[node[i] ]=p[ node[i] ][node[0] ];
if(cnt[node[i] ]>cnt[ node[maxi] ])
{
maxi=i;
}
}
int pre = 0;
for(int s=1;s<n;s++)
{
if(s==n-1)
{
ans=min(ans,cnt[node[maxi] ]);
for(int k=0;k<n;k++)
p[node[k] ][node[pre] ] =p[node[pre] ][node [k] ] += p[node[k] ][node[maxi] ];
node[maxi] = node[--n];
}
vis[node[maxi] ] =1;
pre=maxi;
maxi=-1;
for(int i=0;i<n;i++)
{
if(!vis[node[i]])
{
cnt[node[i] ] += p[node[i] ][node[pre] ];
if(maxi==-1 || cnt[node[i] ]>cnt[node[maxi] ])
{
maxi = i;
}
}
}
}
}
printf("%d\n",ans);
return 0;
}





















 7711
7711











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








