单调队列优化dp 入门 洛谷P2627 修剪草坪

https://www.luogu.org/problem/P2627

题意：给一个长度为nn的数组。现在让你选一些数，并且选的数中不能有在数组中长度超过kk的连续段。求选出的数的和的最大值。

分析：共三种解决方案。

Solution One

顺推.

令 dp[i][0] 表示在前 i 头奶牛中,选了第 i 头奶牛能获得的最大效率

dp[i][1] 表示在前 i 头奶牛中,不选第 i 头奶牛能获得的最大效率

显然可以得出以下转移方程 ( 注意 K 是题目给出的区间长度)

$dp[i][0]=max(dp[i-1][0],dp[i-1][1])$

$dp[i][1]=max\{dp[j][0]+\sum\limits_{j=i-K+1}^{i}E_j \}$

可以预处理出前缀和优化掉一重循环,转移方程就变成了如下所示

$dp[i][1]=max\{dp[j][0]+Sum[i]-Sum[j]\}$

因为最终都要加上一个 Sum[i] ,所以可以把 Sum[i] 移到 max函数外,所以

$dp[i][1]=max\{dp[j][0]-Sum[j]\}+Sum[i]\ \ \ (i-K\leq j < i)$

 

这时候我们可以发现,要使 dp[i][1] 最大,我们就要让 dp[ j ][ 0 ]-Sum[ j ] 尽可能的大,所以只需要用一个单调队列维护长度为 K 的区间中 dp[ j ][ 0 ]-Sum[ j ]dp[ j ][ 0 ]−Sum[ j ] 的最大值就好了.

维护过程还要注意队列中初始就要设置一个val=0，ind=0 的元素表示不减少，然后每次都往单调队列里添加元素，而不是用 i >= K 后再往队列里加，否则会少掉不选前 K 个的最优解情况。

#include <cstdio>
 2 #include <iostream>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 using namespace std;
 7 
 8 typedef long long ll;
 9 const int maxn = 1e6+7;
10 ll a[maxn];
11 ll sum[maxn];
12 ll dp[maxn][2];
13 struct node{
14     int ind;
15     ll val;
16 }que[maxn];
17 
18 
19 int main(){
20     int n,k;
21     scanf("%d%d",&n,&k);
22     for(int i=1; i<=n; i++){
23         scanf("%d",a+i);
24         sum[i] = sum[i-1] +a[i];
25     }
26 
27     int head=0,tail=1;
28     que[0].val = 0;
29     que[0].ind = 0;
30     for(int i=1; i<=n; i++){
31         dp[i][0] = max(dp[i-1][0],dp[i-1][1] );
32 
33         while(head<tail && que[head].ind<=i-k-1) {head++;}
34         while(head<tail && que[tail-1].val<(dp[i][0]-sum[i]) ) tail--;
35         que[tail].val = dp[i][0]-sum[i];
36         que[tail++].ind = i;
37 
38         dp[i][1] = que[head].val+sum[i];
39         
40         // printf("ans=%lld\n", dp[i][1]);
41     }
42 
43     printf("%lld\n", max(dp[n][0],dp[n][1]));
44 }

View Code

 

 

Solution Two

顺推.但状态和之前描述的有些不同

令 dp[i] 表示到前 i 头奶牛为止能得到的最大效率

我们可以在区间 [i−K,i] 间枚举休息的奶牛,所以转移方程就可以初步推出

$ dp[i]=max\{dp[j-1]+\sum\limits_{k=j+1}^{i}E_k\}\ \ \ (i-K\leq j\leq i)  $

同样,我们预处理出前缀和进行优化

$ dp[i]=max\{dp[j-1]+Sum[i]-Sum[j]\}\ \ \ (i-K\leq j\leq i) $

然后也是把  Sum[i]  移到外面

$dp[i]=max\{dp[j-1]-Sum[j]\}+Sum[i]\ \ \ (i-K\leq j\leq i)$

我们发现,这里又可以用一个单调队列维护 dp[j-1]-Sum[j]  ,问题也就迎刃而解了.

 （本质上，就是状态只用 到前几头奶牛 表示，然后通过枚举休息的那只奶牛确定这个位置的最大效率，接着顺推就可以正确dp下去了

    并且，每个位置到前 k 个位置，必须有一头牛休息，因此就有枚举范围了，求值时就是枚举休息的牛的前一头的dp值加上后一头牛到 i 位置的区间的总和。）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;
const int maxn=1e5+7;
ll dp[maxn];
int e[maxn];
ll sum[maxn];
struct node{
    ll val;
    int ind;
}que[maxn];

int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1; i<=n; i++){
        scanf("%d",e+i);
        sum[i] = sum[i-1]+e[i];
    }
    int head=0,tail=1;
    que[0].val=0;
    que[0].ind=0;
    for(int i=1; i<=n; i++){
        while(head<tail && que[head].ind<i-k) head++;
        while(head<tail && que[tail-1].val<dp[i-1]-sum[i]) tail--;  //..tail又漏了-1
        que[tail].ind=i;
        que[tail++].val=dp[i-1]-sum[i];

        dp[i] = que[head].val+sum[i];
    }
    printf("%lld\n", dp[n]);
}

View Code

 

 

Solution Three

逆推,正难则反.

重点讲逆推法

由于题目要求区间 [1,N] 中不能有连续超过 K 头的奶牛,也就是两头休息的奶牛间的距离是 >=K 的 (这里的"距离"指奶牛的数量,单位 1 即为一头奶牛),并且我们要求的是能获得的最大的效率,反过来想,也就是当损失的效率值越少时,能获得的效率也就越大,所以我们可以将问题转化为求出最小的效率损失.

想到这里,dp 的模型就很自然而然地出来了

令 dp[i] 表示前 i 头奶牛且第 i 头奶牛不工作时的最小损失

则状态转移方程为

$dp[i]=min\{dp[j]\}+E[i]\ \ \ (i-K-1\leq j<i)$

这里 j 的左边界为 i−K−1 而不是 i−K 的原因是如果不选第 i 头奶牛则上一头休息的奶牛的位置就是 i−K−1 ,也就是说,此时我们单调队列维护的是长度为 K+1 的区间中 dp[j] 的最小值.

另外,这里有个小技巧就是最后一段区间的奶牛可能全都不休息,所以我们可以加一个编号为 N+1 的虚点,最终答案即为 

 

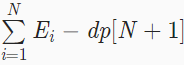
 (可以画下图理解区间范围为 K+1 )

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;
const int maxn=1e5+7;
ll dp[maxn];
int e[maxn];
struct node{
    ll val;
    int ind;
}que[maxn];

int main(){
    int n,k;
    ll sum=0;
    scanf("%d%d",&n,&k);
    for(int i=1; i<=n; i++){
        scanf("%d",e+i);
        sum += e[i];
    }
    int head=1,tail=1;
    que[1].ind = 0;
    que[1].val = 0;
    for(int i=1; i<=n+1; i++){          //要考虑到最后几头都选取的情况，就来个虚拟的第n+1头牛就好了
        dp[i] = que[head].val + e[i];
        // printf("%lld\n", que[head].val);
        while(head<=tail && que[head].ind<=i-k-1) head++;
        while(head<=tail && que[tail].val>dp[i]) tail--;   /
        que[++tail].val = dp[i];
        que[tail].ind = i;
    }

    printf("%lld\n", sum-dp[n+1]);
}

View Code

 

 

 

 

转载于:https://www.cnblogs.com/-Zzz-/p/11409934.html