深入浅出计算机组成原理16-浮点数和定点数（下）：深入理解浮点数到底有什么用？

浮点数的二进制转化

我们首先来看，十进制的浮点数怎么表示成二进制。

我们输入一个任意的十进制浮点数，背后都会对应一个二进制表示。比方说，我们输入了一个十进制浮点数 9.1。那么按照之前的讲解，在二进制里面，我们应该把它变成一个“符号位 s+ 指数位 e+ 有效位数 f”的组合。第一步，我们要做的，就是把这个数变成二进制。

首先，我们把这个数的整数部分，变成一个二进制。这个我们前面讲二进制的时候已经讲过了。这里的 9，换算之后就是 1001。

接着，我们把对应的小数部分也换算成二进制。小数怎么换成二进制呢？我们先来定义一下，小数的二进制表示是怎么回事。我们拿 0.1001 这样一个二进制小数来举例说明。和上面的整数相反，我们把小数点后的每一位，都表示对应的 2 的 -N 次方。那么 0.1001，转化成十进制就是：

1×2⁻¹+0×2⁻²+0×2⁻³+1×2⁻⁴=0.5625

和整数的二进制表示采用“除以 2，然后看余数”的方式相比，小数部分转换成二进制是用一个相似的反方向操作，就是乘以 2，然后看看是否超过 1。如果超过 1，我们就记下 1，并把结果减去 1，进一步循环操作。在这里，我们就会看到，0.1 其实变成了一个无限循环的二进制小数，0.000110011。这里的“0011”会无限循环下去。

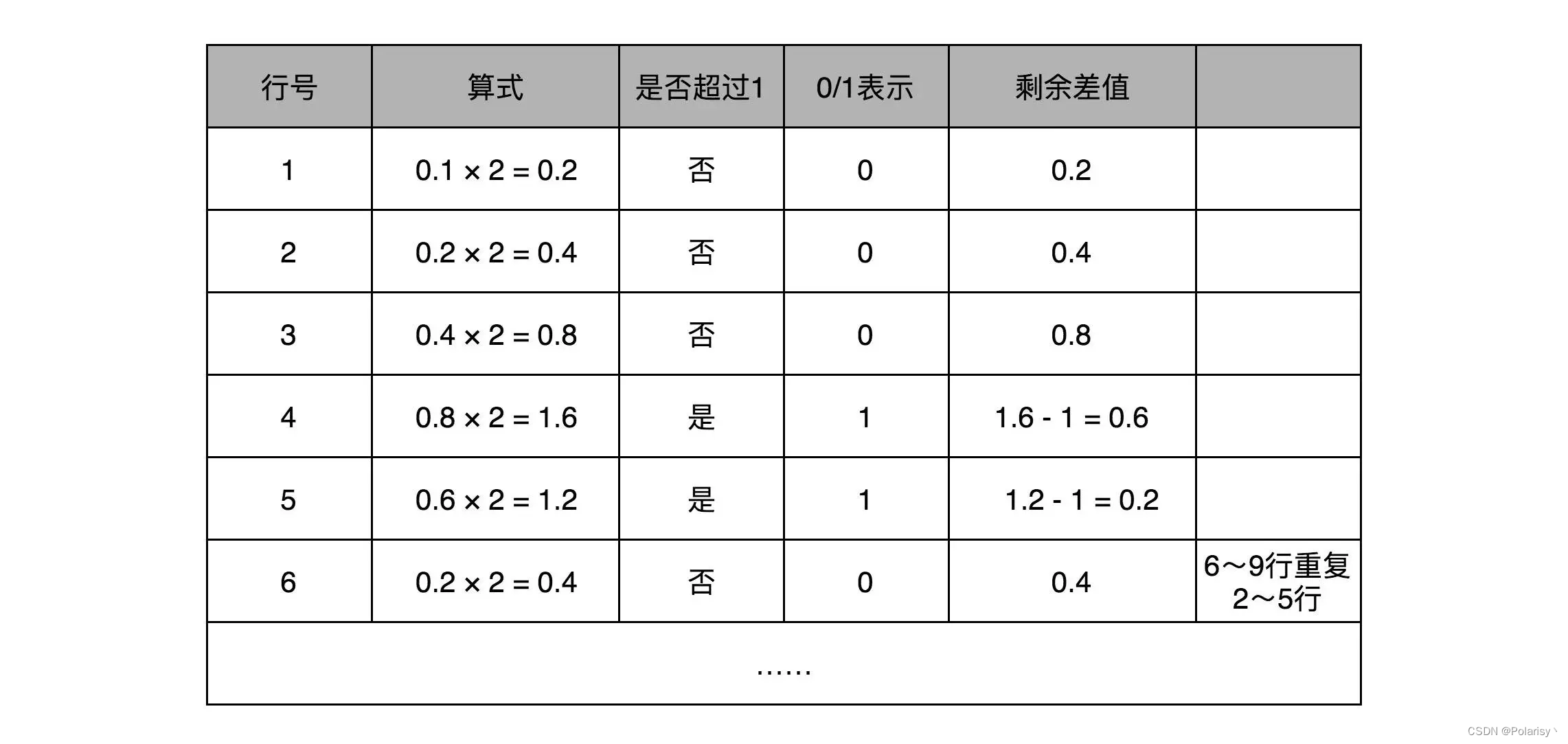
然后，我们把整数部分和小数部分拼接在一起，9.1 这个十进制数就变成了 1001.000110011…这样一个二进制表示。

上一讲我们讲过，浮点数其实是用二进制的科学计数法来表示的，所以我们可以把小数点左移三位，这个数就变成了：

1.001000110011…×2³

那这个二进制的科学计数法表示，我们就可以对应到了浮点数的格式里了。这里的符号位 s = 0，对应的有效位 f=001000110011…。因为 f 最长只有 23 位，那这里“0011”无限循环，最多到 23 位就截止了。于是，f=00100011001100110011 001。最后的一个“0011”循环中的最后一个“1”会被截断掉。对应的指数为 e，代表的应该是 3。因为指数位有正又有负，所以指数位在 127 之前代表负数，之后代表正数，那 3 其实对应的是加上 127 的偏移量 130，转化成二进制，就是 130，对应的就是指数位的二进制，表示出来就是 10000010。

然后，我们把“s+e+f”拼在一起，就可以得到浮点数 9.1 的二进制表示了。最终得到的二进制表示就变成了：

010000010 0010 0011001100110011 001

如果我们再把这个浮点数表示换算成十进制， 实际准确的值是 9.09999942779541015625。相信你现在应该不会感觉奇怪了。

这个也解释了为什么，在上一讲一开始，0.3+0.6=0.899999。因为 0.3 转化成浮点数之后，和这里的 9.1 一样，并不是精确的 0.3 了，0.6 和 0.9 也是一样的，最后的计算会出现精度问题。

浮点数的加法和精度损失

搞清楚了怎么把一个十进制的数值，转化成 IEEE-754 标准下的浮点数表示，我们现在来看一看浮点数的加法是怎么进行的。其实原理也很简单，你记住六个字就行了，那就是先对齐、再计算。

两个浮点数的指数位可能是不一样的，所以我们要把两个的指数位，变成一样的，然后只去计算有效位的加法就好了。

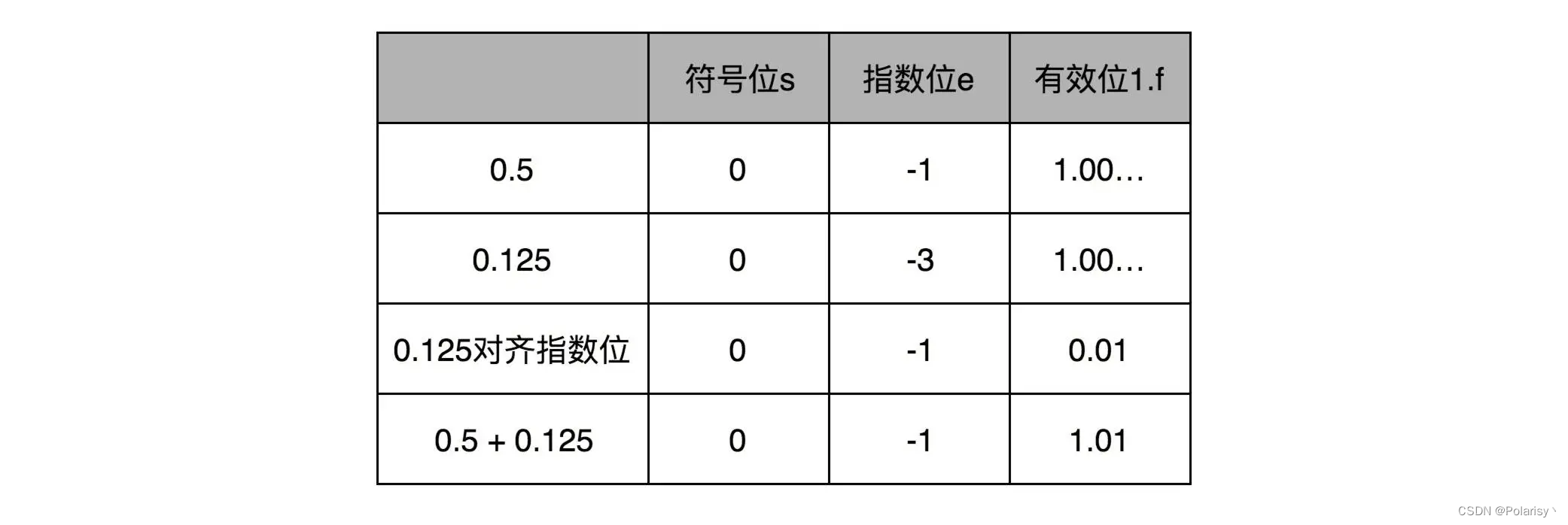
比如 0.5，表示成浮点数，对应的指数位是 -1，有效位是 00…（后面全是 0，记住 f 前默认有一个 1）。0.125 表示成浮点数，对应的指数位是 -3，有效位也还是 00…（后面全是 0，记住 f 前默认有一个 1）。

那我们在计算 0.5+0.125 的浮点数运算的时候，首先要把两个的指数位对齐，也就是把指数位都统一成两个其中较大的 -1。对应的有效位 1.00…也要对应右移两位，因为 f 前面有一个默认的 1，所以就会变成 0.01。然后我们计算两者相加的有效位 1.f，就变成了有效位 1.01，而指数位是 -1，这样就得到了我们想要的加法后的结果。

指数位为什么是小阶对大阶？指数位从-3对齐至-1，有效位则需要对应右移两位；显然，从-1对齐至-3，有效位则需要对应左移两位，此时带来的精度损失比右移通常要大。所以，指数位对阶的原则是小阶对大阶。

实现这样一个加法，也只需要位移。和整数加法类似的半加器和全加器的方法就能够实现，在电路层面，也并没有引入太多新的复杂性。

回到浮点数的加法过程，你会发现，其中指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。两个相加数的指数位差的越大，位移的位数越大，可能丢失的精度也就越大。当然，也有可能你的运气非常好，右移丢失的有效位都是 0。这种情况下，对应的加法虽然丢失了需要加的数字的精度，但是因为对应的值都是 0，实际的加法的数值结果不会有精度损失。

32 位浮点数的有效位长度一共只有 23 位，如果两个数的指数位差出 23 位，较小的数右移 24 位之后，所有的有效位就都丢失了。这也就意味着，虽然浮点数可以表示上到 3.40×10³⁸，下到 1.17×10⁻³⁸ 这样的数值范围。但是在实际计算的时候，只要两个数，差出 2²⁴，也就是差不多 1600 万倍，那这两个数相加之后，结果完全不会变化。

你可以试一下，我下面用一个简单的 Java 程序，让一个值为 2000 万的 32 位浮点数和 1 相加，你会发现，+1 这个过程因为精度损失，被“完全抛弃”了。

public class FloatPrecision {
  public static void main(String[] args) {
    float a = 20000000.0f;
    float b = 1.0f;
    float c = a + b;
    System.out.println("c is " + c);
    float d = c - a;
    System.out.println("d is " + d);
  }
}

对应的输出结果就是：

c is 2.0E7
d is 0.0

Kahan Summation 算法

那么，我们有没有什么办法来解决这个精度丢失问题呢？虽然我们在计算浮点数的时候，常常可以容忍一定的精度损失，但是像上面那样，如果我们连续加 2000 万个 1，2000 万的数值都会被精度损失丢掉了，就会影响我们的计算结果。

一个常见的应用场景是，在一些“积少成多”的计算过程中，比如在机器学习中，我们经常要计算海量样本计算出来的梯度或者 loss，于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大，但是随着累积值的越来越大，就会出现“大数吃小数”的情况。

我们可以做一个简单的实验，用一个循环相加 2000 万个 1.0f，最终的结果会是 1600 万左右，而不是 2000 万。这是因为，加到 1600 万之后的加法因为精度丢失都没有了。这个代码比起上面的使用 2000 万来加 1.0 更具有现实意义。

public class FloatPrecision {
  public static void main(String[] args) {
    float sum = 0.0f;
    for (int i = 0; i < 20000000; i++) {
      float x = 1.0f;
      sum += x;      
    }
    System.out.println("sum is " + sum);   
  }  
}

对应的输出结果是：

sum is 1.6777216E7

面对这个问题，聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题。算法的对应代码我也放在文稿中了。从中你可以看到，同样是 2000 万个 1.0f 相加，用这种算法我们得到了准确的 2000 万的结果。

public class KahanSummation {
  public static void main(String[] args) {
    float sum = 0.0f;
    float c = 0.0f;
    for (int i = 0; i < 20000000; i++) {
      float x = 1.0f;
      float y = x - c;
      float t = sum + y;
      c = (t-sum)-y;
      sum = t;      
    }
    System.out.println("sum is " + sum);   
  }  
}

对应的输出结果就是：

sum is 2.0E7

其实这个算法的原理其实并不复杂，就是在每次的计算过程中，都用一次减法，把当前加法计算中损失的精度记录下来，然后在后面的循环中，把这个精度损失放在要加的小数上，再做一次运算。

总结延伸

到这里，我们已经讲完了浮点数的表示、加法计算以及可能会遇到的精度损失问题。可以看到，虽然浮点数能够表示的数据范围变大了很多，但是在实际应用的时候，由于存在精度损失，会导致加法的结果和我们的预期不同，乃至于完全没有加上的情况。

所以，一般情况下，在实践应用中，对于需要精确数值的，比如银行存款、电商交易，我们都会使用定点数或者整数类型。

比方说，你一定在 MySQL 里用过 decimal(12,2)，来表示订单金额。如果我们的银行存款用 32 位浮点数表示，就会出现，马云的账户里有 2 千万，我的账户里只剩 1 块钱。结果银行一汇总总金额，那 1 块钱在账上就“不翼而飞”了。

而浮点数呢，则更适合我们不需要有一个非常精确的计算结果的情况。因为在真实的物理世界里，很多数值本来就不是精确的，我们只需要有限范围内的精度就好了。比如，从我家到办公室的距离，就不存在一个 100% 精确的值。我们可以精确到公里、米，甚至厘米，但是既没有必要、也没有可能去精确到微米乃至纳米。