Stata：异质性DID代码详解

阅读全文：Stata：异质性DID代码详解

作者：严安冬 (加州大学河滨分校)  
邮箱：ayan013@ucr.edu

 

编者注：本文由原作者在 Di Liu 博士于 Stata Webinar 展示的异质性 DID 课程的基础上，对代码细节进行了解释并提供了案例。原 Stata Webinar 可以通过 Webinars | Stata (注册后可以浏览) 找到，译者将课程视频和 PDF 文件的链接附在下面

• Recording
• Course materials (.pdf)

Source：Saadaoui, J., 2023, Blog, Heterogeneous Difference-in-Differences with Stata -Link-

 

1. 回顾 TWFE 模型的问题

我们首先考虑双重固定效应 (TWFE) 模型下可能出现的问题：

yit=θt+ηi+ditα+νityit​=θt​+ηi​+dit​α+νit​

其中处理效应的估计量可以分解为：

α=∑wkGoodDIDk+∑wjBadDIDjα=∑wk​GoodDIDk​+∑wj​BadDIDj​

我们考虑三种不同的控制组与处理组的比较情形：

1. 新处理组 vs 控制组 (从不处理组) (良好)
2. 新处理组 vs 尚未处理组 (良好)
3. 新处理组 vs 已经处理组 (差)

在上述模型中，我们用 ditdit​ 作为虚拟变量来表示个体 ii 在时间 tt 期是否受到了处理。我们需要了解在上述的双重固定效应的估计量中，它可能混合了“好”的比较 (情况 1 和情况 2) 和“坏”的比较 (情况 3)。原因在于，当我们将新处理组与对照组 (情况 1) 和尚未处理组 (情况 2) 进行比较时，我们是能够识别处理效应的，这样的控制对照是“好”的。然而，当处理效应存在异质性时，将新处理组与已经处理组 (情况 3) 进行比较是存在偏误的，而这时的控制对照是“坏”的。

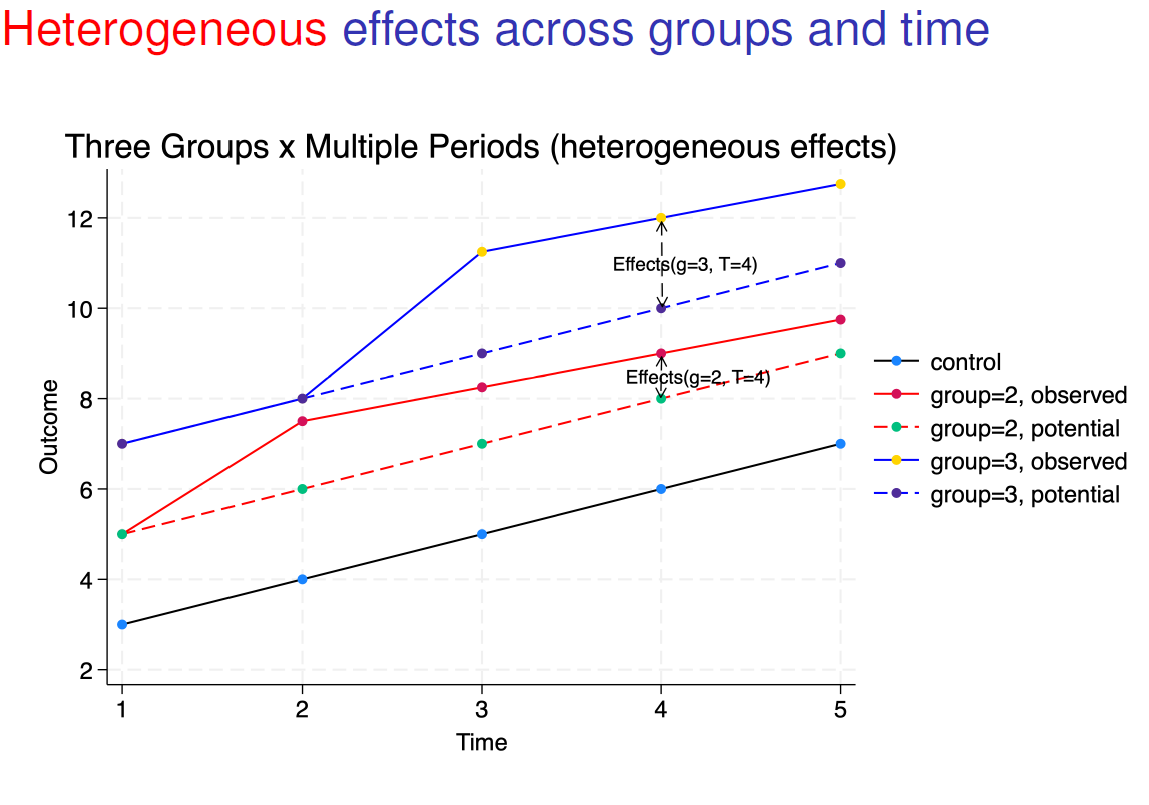
TWFE 估计量在存在异质性效果的情况下，是对“好”比较和“坏”比较的加权平均，并且它打破了平行趋势假设，所以得到的估计量是可能存在偏误的 (上图中的实蓝线与实红线对比；红色组为早处理组，蓝色组为晚处理组，且蓝色组和红色组的处理效应系数不同，存在异质性)。在同质性效果的情况下，如下图所示，TFWE 估计量是有效的，因为平行趋势假设成立，你可以通过比较从 T = 3 期开始处理的实蓝线和实红线来获得对处理组 3 的平均效果 (在上一张图中，存在异质性效果的情况下，两条线并不平行) 。

 

2. Stata 18 中异质性 DID 的新指令

2.1 实证案例及作图

在 Stata 18 中，新增了两个指令 xthdidregress 和 hdidregress，分别用于面板数据和重复截面数据的估计。这两个指令提供了四种估计量的选择，分别是由 Callaway and Sant’Anna (2021) 提出的 ra，ipw，aipw，以及由 Wooldridge (2021) 提出的 twfe。

这些新指令的使用可以通过以下案例来加以阐释 (本案例为Callaway and Sant’Anna (2021) 论文中的第五节的实证分析)：考虑的结果变量为美国县级的青年就业率，处理变量为州政府实施的最低工资政策。数据涵盖了 2002 年至 2007 年的多期数据，其中处理发生在 2004 年、2006 年和 2007 年这三个时间点。

2.2 ATET 结果

我们用 xthdidregress 作为例子，以下是 指令的实现代码：

# Define Covariates 定义协变量
global covars i.region pop medinc white hs pov c.pop#c.pop c.medinc#c.medinc

# Use AIPW estimator 使用AIPW估计量
xthdidregress aipw (lemp $covars) (treat $covars), group(state)

在这里，我们控制了协变量来保证条件平行趋势，回归总共会有 18 个组与时间的 ATET 估计值 (6 年 ×× 3 组)，标准误在州的层级上进行聚类调整。我们可以用 atetplot 指令得到对处理组的平均处理效应 (ATET) 的趋势图：

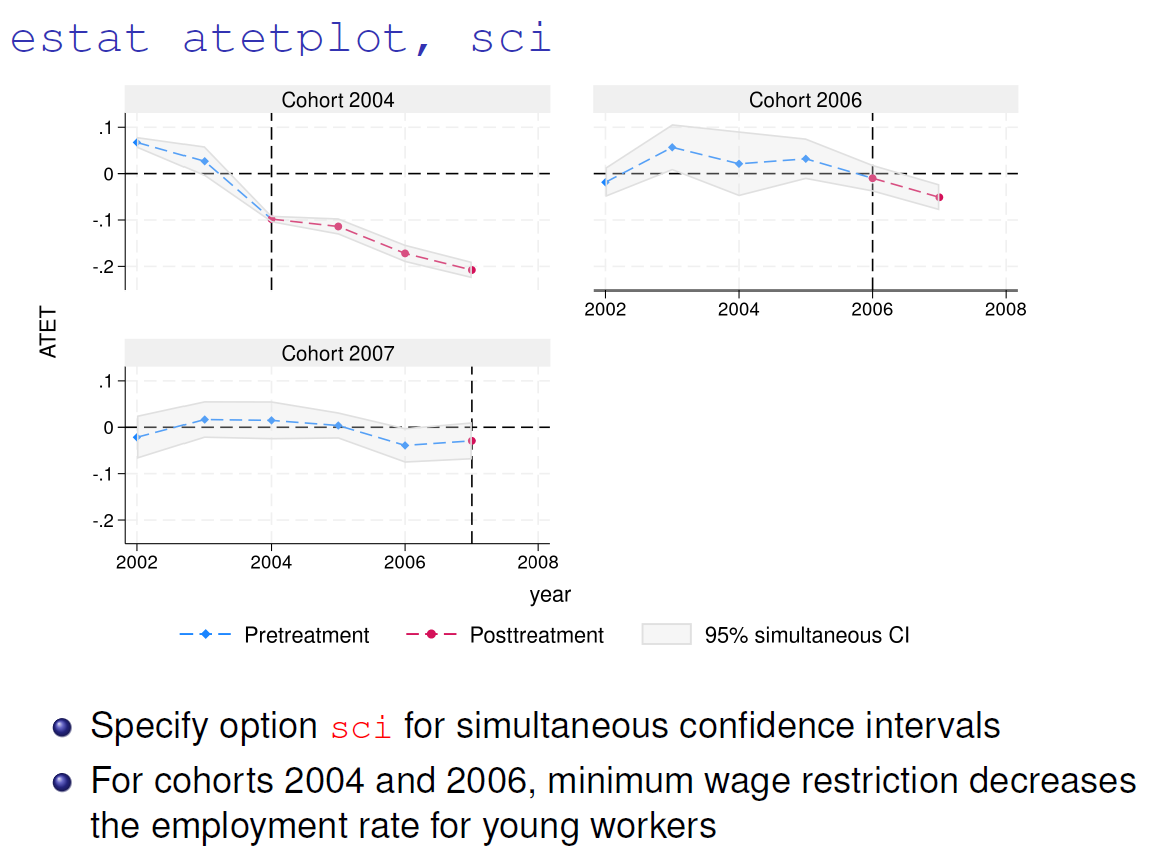
estat atetplot, sci

其中，我们使用 sci 选项来同时得到置信区间。结果如下图所示：

 阅读全文：Stata：异质性Stata：