Tarjan 算法

Tarjan 算法

一.算法简介

Tarjan 算法一种由Robert Tarjan提出的求解有向图强连通分量的算法，它能做到线性时间的复杂度。

 

我们定义：

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

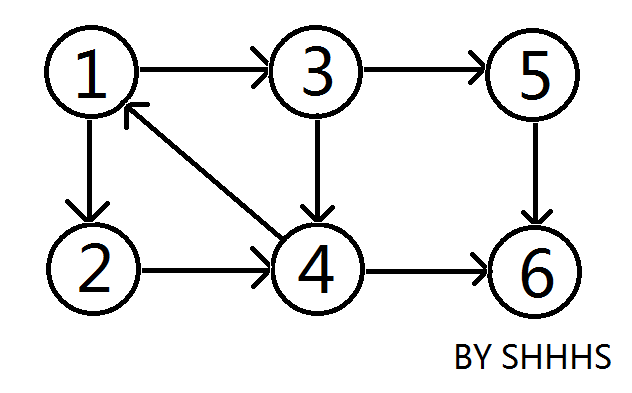
例如：在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

再Tarjan算法中，有如下定义。

DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

 

二.算法图示

以1为Tarjan 算法的起始点，如图

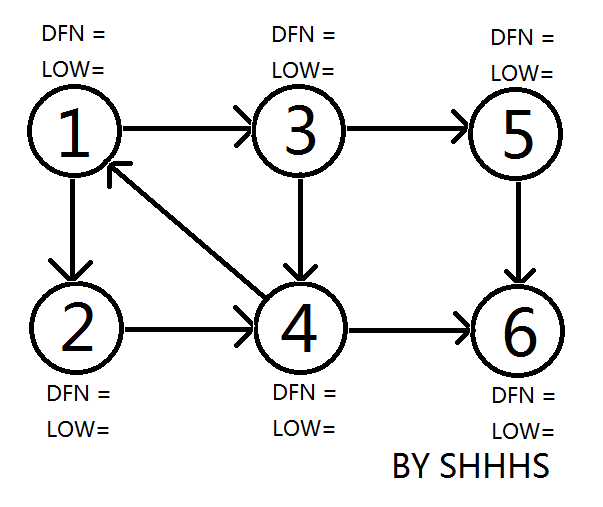
顺次DFS搜到节点6

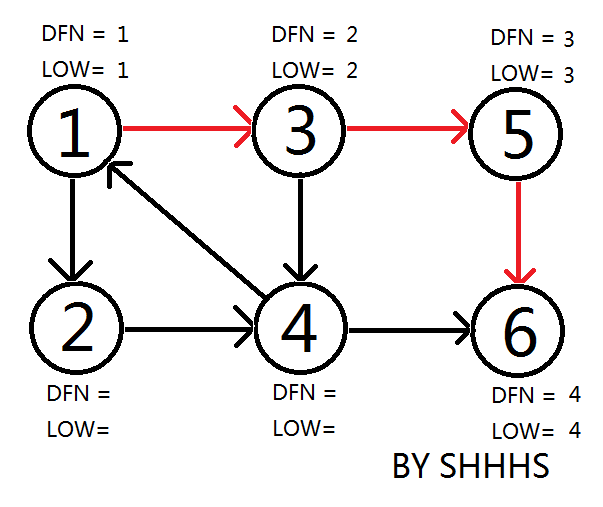
 回溯时发现LOW[ 5 ]==DFN[ 5 ] ,  LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

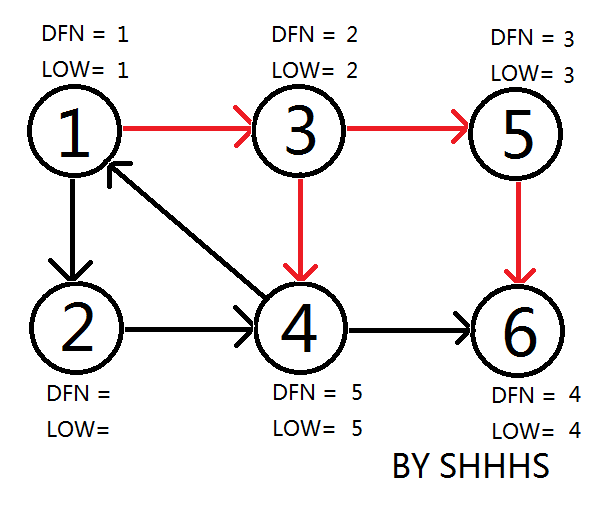
拓展节点1 ， 发现1再栈中更新LOW[ 4 ]，LOW[ 3 ] 的值为1

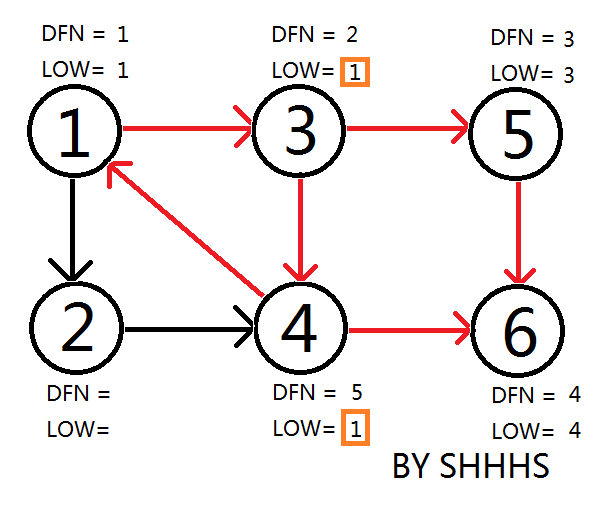
 回溯节点1，拓展节点2

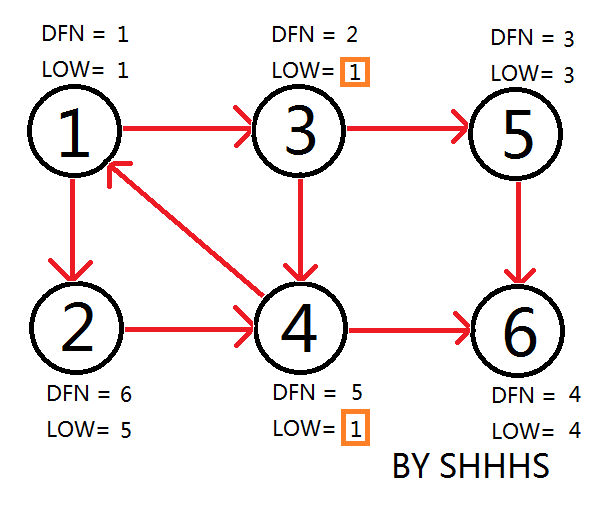
自此，Tarjan Algorithm 结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

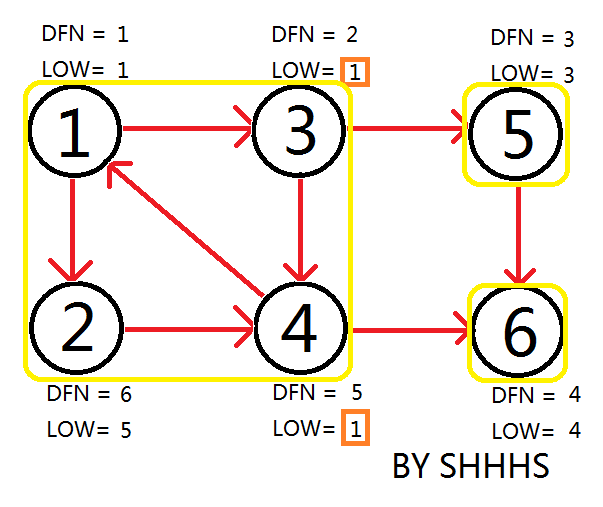
不难发现，Tarjan Algorithm 的时间复杂度为O(E+V).

三.算法模板

 1 void Tarjan ( int x ) {
 2          dfn[ x ] = ++dfs_num ;
 3          low[ x ] = dfs_num ;
 4          vis [ x ] = true ;//是否在栈中
 5          stack [ ++top ] = x ;
 6          for ( int i=head[ x ] ; i!=0 ; i=e[i].next ){
 7                   int temp = e[ i ].to ;
 8                   if ( !dfn[ temp ] ){
 9                            Tarjan ( temp ) ;
10                            low[ x ] = gmin ( low[ x ] , low[ temp ] ) ;
11                  }
12                  else if ( vis[ temp ])low[ x ] = gmin ( low[ x ] , dfn[ temp ] ) ;
13          }
14          if ( dfn[ x ]==low[ x ] ) {//构成强连通分量
15                   vis[ x ] = false ;
16                   color[ x ] = ++col_num ;//染色
17                   while ( stack[ top ] != x ) {//清空
18                            color [stack[ top ]] = col_num ;
19                            vis [ stack[ top-- ] ] = false ;
20                  }
21                  top -- ;
22          }
23 }

 

注：本文章上部分内容转载自http://www.cppblog.com/sosi/archive/2010/09/26/127797.html；一方面是网上有很多关于tarjan算法的介绍，我觉得都没有这个他的文章介绍的简明易懂或者没有具体的实现。另一方面，自己也顺便用java实现了一下，所以发表出来和大家分享分享!

 

[有向图强连通分量]

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

 

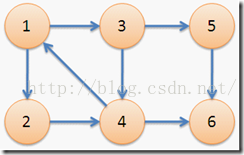
[Tarjan算法]

Tarjan算法是基于对图深度优

定义DFN(u)D记录搜索到该u的时间，也就是第几个搜索u的。Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

 

 

算法伪代码如下

tarjan(u)
{

    DFN[u]=Low[u]=++Index     // 为节点u设定次序编号和Low初值

    Stack.push(u)                     // 将节点u压入栈中

    for each (u, v) in E               // 枚举每一条边

          if (v is not visted)          // 如果节点v未被访问过

                  tarjan(v)              // 继续向下找

                  Low[u] = min(Low[u], Low[v])

            else if (v in S)            // 如果节点v还在栈内

            Low[u] = min(Low[u], DFN[v])

    if (DFN[u] == Low[u])        // 如果节点u是强连通分量的根

       repeat

           v = S.pop                  // 将v退栈，为该强连通分量中一个顶点

           print v

      until (u== v)

}

 

 

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

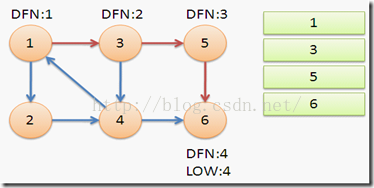
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

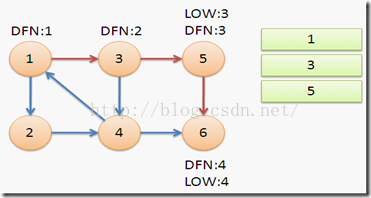
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

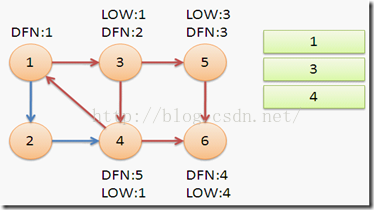
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

 

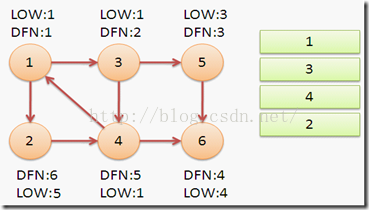
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

算法java实现如下：

Tarjan类：

 

1. import java.util.ArrayList;

2. import java.util.Arrays;

3. import java.util.List;

4. import java.util.Stack;

5.  
6.  

7. public class Tarjan {

8. private int numOfNode;

9. private List< ArrayList<Integer> > graph;//图

10. private List< ArrayList<Integer> > result;//保存极大强连通图

11. private boolean[] inStack;//节点是否在栈内，因为在stack中寻找一个节点不方便。这种方式查找快

12. private Stack<Integer> stack;

13. private int[] dfn;

14. private int[] low;

15. private int time;//

16.  

17. public Tarjan(List< ArrayList<Integer> > graph,int numOfNode){

18. this.graph = graph;

19. this.numOfNode = numOfNode;

20. this.inStack = new boolean[numOfNode];

21. this.stack = new Stack<Integer>();

22. dfn = new int[numOfNode];

23. low = new int[numOfNode];

24. Arrays.fill(dfn, -1);//将dfn所有元素都置为-1，其中dfn[i]=-1代表i还有没被访问过。

25. Arrays.fill(low, -1);

26. result = new ArrayList<ArrayList<Integer>>();

27. }

28.  

29. public List< ArrayList<Integer> > run(){

30. for(int i=0;i<numOfNode;i++){

31. if(dfn[i]==-1){

32. tarjan(i);

33. }

34. }

35. return result;

36. }

37.  

38. public void tarjan(int current){

39. dfn[current]=low[current]=time++;

40. inStack[current]=true;

41. stack.push(current);

42.  

43. for(int i=0;i<graph.get(current).size();i++){

44. int next = graph.get(current).get(i);

45. if(dfn[next]==-1){//-1代表没有被访问

46. tarjan(next);

47. low[current]=Math.min(low[current], low[next]);

48. }else if(inStack[next]){

49. low[current]=Math.min(low[current], dfn[next]);

50. }

51. }

52.  

53. if(low[current]==dfn[current]){

54. ArrayList<Integer> temp =new ArrayList<Integer>();

55. int j = -1;

56. while(current!=j){

57. j = stack.pop();

58. inStack[j]=false;

59. temp.add(j);

60. }

61. result.add(temp);

62. }

63. }

64.  

65. }

66.  
67.  

测试类：

 

 

1. import java.util.ArrayList;

2. import java.util.List;

3. import java.util.Stack;

4.  
5.  

6. public class Main {

7. public static void main(String[] args) {

8. //创建图

9. int numOfNode = 6;

10. List< ArrayList<Integer> > graph = new ArrayList<ArrayList<Integer>>();

11. for(int i=0;i<numOfNode;i++){

12. graph.add(new ArrayList<Integer>());

13. }

14. graph.get(0).add(1);

15. graph.get(0).add(2);

16. graph.get(1).add(3);

17. graph.get(2).add(3);

18. graph.get(2).add(4);

19. graph.get(3).add(0);

20. graph.get(3).add(5);

21. graph.get(4).add(5);

22. //调用Tarjan算法求极大连通子图

23. Tarjan t = new Tarjan(graph, numOfNode);

24. List< ArrayList<Integer> > result = t.run();

25. //打印结果

26. for(int i=0;i<result.size();i++){

27. for(int j=0;j<result.get(i).size();j++){

28. System.out.print(result.get(i).get(j)+" ");

29. }

30. System.out.println();

31. }

32.  

33. }

34. }

先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。