计算流体力学简介(七)——频散关系保持(DRP)格式

色散误差

前面的计算中分析了一阶格式的格式粘性，并且提到了一阶格式的格式粘性是泰勒展开的最低阶误差项，因为格式是一阶所以最低阶误差就是二阶项，表现为粘性，因此称为格式粘性。但是前面也有提到泰勒展开的误差项中偶数阶误差项表现为耗散，奇数阶表现为色散。因此其实一阶格式的最高阶误差应当分为奇数阶和偶数阶分别分析。当保留三阶误差项时即可得到一个色散项。这个色散项会使得各频率分量以不同与微分方程描述的传播速度运动，最终经过长时间的推进积累，个频率分量就会分离，产生类似三棱镜对太阳光的作用，因此称为色散。由于一阶迎风格式的耗散很大，在出现明显色散之前就能力就耗散完了，因此这里使用中心差分加人工粘性的做法来简单展示一下色散误差的作用。
具体推进如下
$u_i^{n+1}=u_i^n-\frac{\Delta t}{2\Delta x}(u_{i+1}^n-u_{i-1}^n)+\nu \frac{\Delta t}{\Delta x^2}(u_{i+1}^n-2u_i^n+u_{i-1}^n)$

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
const int NE=20,//空间点数
NS=10000,//时间步数
SKIP_STEP=100;
const double rb=-5,l=10,//计算域左边界，计算域长度
dt=0.2,//时间步长
dx=l/NE;
void init_guass(vector<double> &u0)//设置高斯函数初场
{
    for(int i=0;i<u0.size();i++) 
	{
		u0[i]=exp(-pow((l*double(i)/(NE-1)+rb),2));
	}
}
void advance(vector<double>& u)
{
    vector<double> t(u);
    double nu=0.02;
    for(int i=0;i<u.size()-1;i++)
    {
        u[i]=t[i]-0.5*(t[i+1]-t[i-1])*dt/dx+nu*(t[i+1]-2*t[i]+t[i-1])/(dx*dx);
    }
    int i=u.size()-1;
    u[i]=t[i]-0.5*(t[0]-t[i-1])*dt/dx+nu*(t[0]-2*t[i]+t[i-1])/(dx*dx);
    i=0;
    u[i]=t[i]-0.5*(t[i+1]-t[u.size()-1])*dt/dx+nu*(t[i+1]-2*t[i]+t[u.size()-1])/(dx*dx);
}
ostream& operator<<(ostream& out,const vector<double>& A)
{
        for(int j=0;j<A.size()-1;j++)
        {
            out<<A[j]<<'\t';
        }
        out<<A[A.size()-1];
    return out;
}
int main()
{
    vector<double> u(NE+1);
    init_guass(u);
    cout<<NE+1<<'\t'<<NS/SKIP_STEP<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<u<<'\n';
    for(int i=0;i<NS;i++)
    {
        advance(u);
        if(NS%SKIP_STEP==0)cout<<u<<'\n';
    }
    return 0;
}

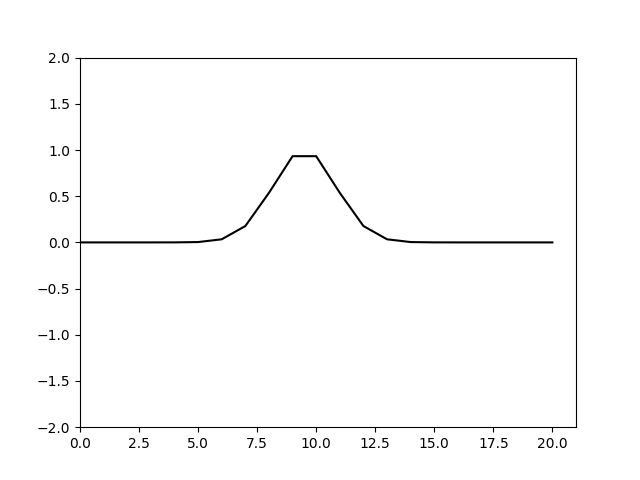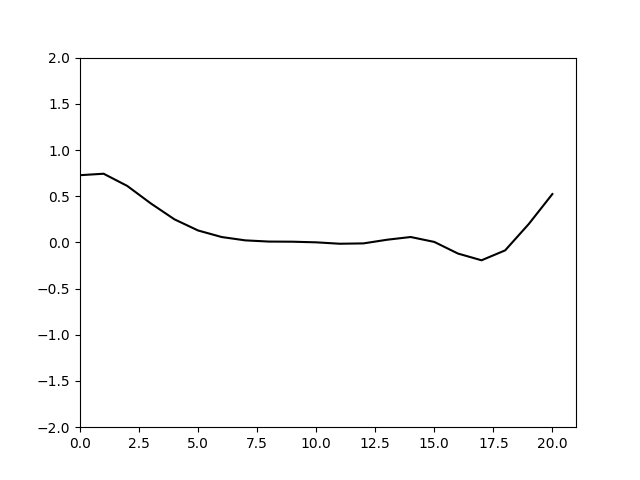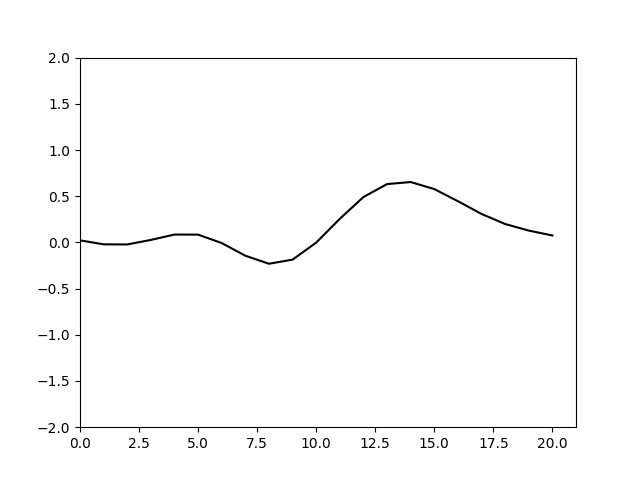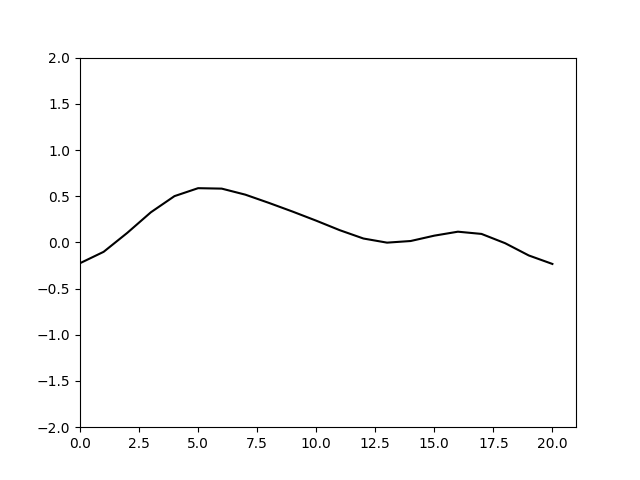
可以看到随着计算的进行不同频率的波形发生了分离，也就是色散。频率越高的信号色散现象越明显，要消除这种色散就要使得空间步长足够小确保可以分辨相应的信号。
在计算声学中，当声源包含很高频信号时，在传播过程中如果色散过于明显则会使得最终得到的声学信号不准确，因此在计算声学中常常对频散关系做一定的调整，使得相同的网格密度($\Delta x$)下可以分辨更高波数的信号。
在计算声学中有一个叫PPW(Points Per Wavelength，每波长网格点数量)的格式参数，用于表示当前格式分辨特定波长时需要的网格点数(例如要分辨无量纲波长为0.1的信号，则需要$\Delta x\le \frac{0.1}{PPW}$)。对于一个特定的差分格式，它的PPW越小，就表明其保证高波数(低波长)不发生明显色散所需要的网格数量更少。

基本原理

经典的DRP格式是七点格式，这里为了简单，推导五点格式。因为DRP格式的目的是消除色散误差，因此以没有耗散误差的中心差分格式为基础来进行频散关系优化。
正常五点中心差分格式的阶数是四阶，要满足优化频散关系就需要降阶，为了满足中心差分的对称性，因此五点中心差分格式实际上只有两个参数。这里降阶就是放开一个参数，用于优化频散关系，这样格式会降阶为二阶格式。记五点中心差分的参数分别为$k_1,k_2$则有
$\frac{\partial u}{\partial x}=k_2{u}_{i+2}+k_1{u}_{i+1}-k_1{u}_{i-1}-k_2{u}_{i-2}$
做泰勒展开后偶数阶展开项都会自动消去。一阶展开项系数需满足为
$2k_2+k_1+k_1+2k_2=1$
化简得
$k_1=\frac{1-4k_2}{2}$
对原差分近似做傅里叶变换得到。
$\sum j\alpha a_i{e}^{j\alpha x}=\frac{\sum a_i{e}^{j\alpha x}(k_2{e}^{2j\alpha \Delta x}+k_1{e}^{j\alpha \Delta x}-k_1{e}^{-j\alpha \Delta x}-k_2{e}^{-2j\alpha \Delta x})}{\Delta x}$
两边约去相同的量并将$e^{j\alpha \Delta x}$展开化简后得任意波数$\alpha$应满足
$\alpha \Delta x=2(k_{2}sin(2\alpha \Delta x)+k_{1}sin(\alpha \Delta x))$代入$k_1,k_2$的关系式得到
$\alpha \Delta x=(1-4k_2)sin(\alpha \Delta x)+2k_{2}sin(2\alpha \Delta x)$令误差
$E={\int }_a^b(\alpha \Delta x-2k_{2}sin(2\alpha \Delta x)+(4k_2-1)sin(\alpha \Delta x){)}^{2}d(\alpha \Delta x)$
所以求解DRP格式的系数就变为了求适当的$k_2$使得$E$取得最小值。
在误差$E$中有两个可调参数$a,b$和一个待求参数$k_2$，$a,b$表示格式需要在哪个范围内保持相应的频散关系。误差$E$积分中的函数是偶函数，因此我们直接取$a=0$，而$b$的值越大我们就能让差分近似在更大的区间$[a,b]$上尽可能的接近原本的微分结果，但是通常$b$越大$E$的最小值也会随之增大。例如当$b=\pi /4$时得到的$E_{min}=E_1$，$b=\pi$时得到的$E_{min}=E_2$通常$E_2>E_1$。所以我们应当尽可能保持$b$足够大而$E_{min}$又足够小。
这里取$b=1.2$令$\frac{\partial E}{\partial k_2}=0$解出$$\begin{gathered} {k}_1=0.7090664489143 \\ {k}_2=-0.1045332244572 \end{gathered}$$
将不同格式的相位变化与$\alpha \Delta x$的关系绘制成曲线如下

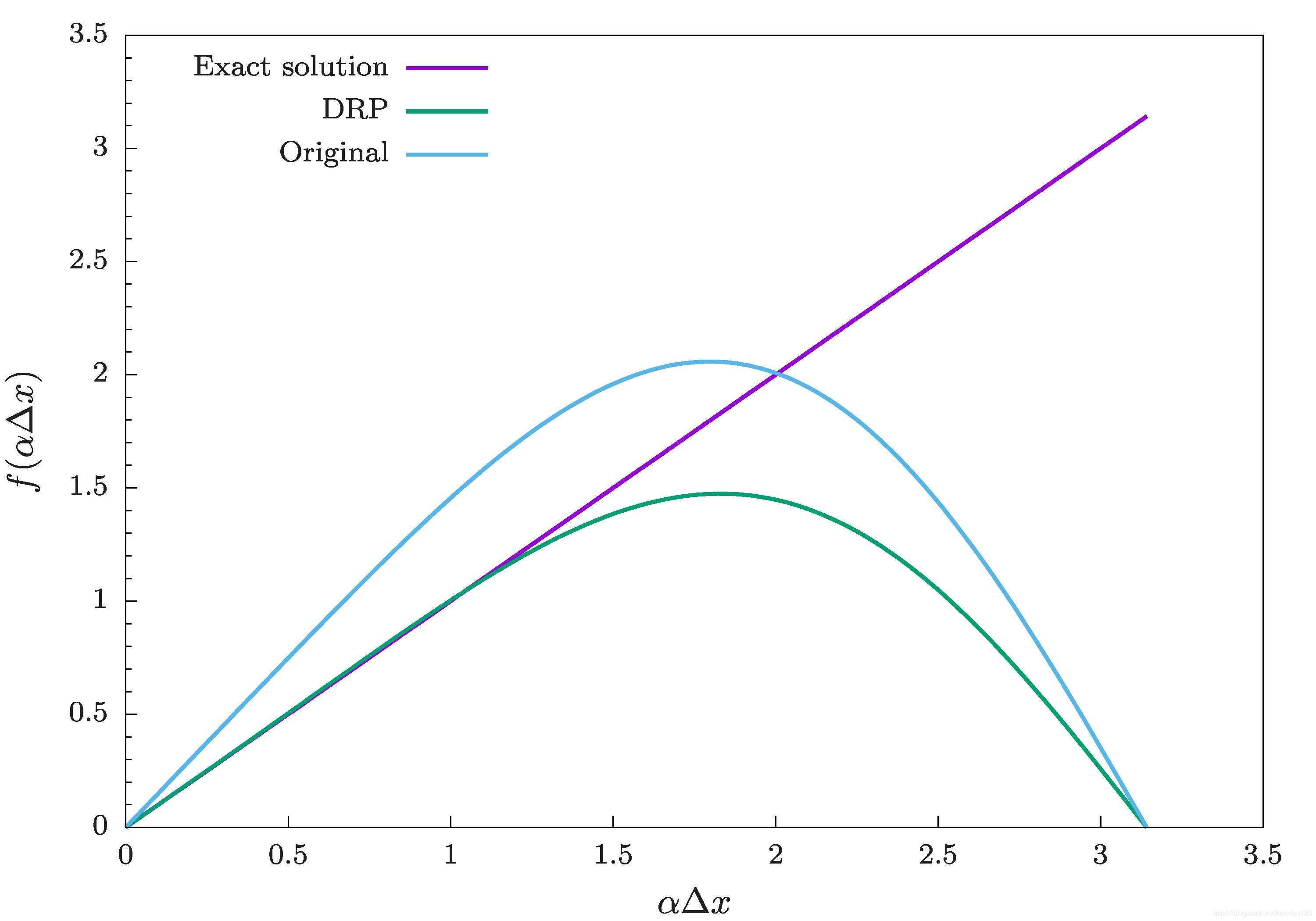
可以看到相比于标准的中心差分格式，DRP格式在$\alpha \Delta x$靠近0的位置更加接近精确解。也就是说DRP格式的频散关系更加接近精确解，因此这种方法构造来的格式称为Dispersion Relation Preserving(频散关系保持)格式。
根据绘制的曲线可以看到经过优化大约在$[0,1.1]$的区间内保证正确的频散关系。由$\alpha =\frac{2\pi }{\lambda }$得到$\frac{2\pi \Delta x}{\lambda }\le 1.1$时频散关系准确。变形后得到$PPW=\frac{\lambda }{\Delta x}\ge \frac{2\pi }{1.1}\approx 6$所以改格式的PPW为6，要分辨的最短波长信号${\lambda }_{min}$，则空间步长最大为$\Delta x=\frac{{\lambda }_{min}}{6}$。
同样的方法也可以通过降阶来获得优化的时间推进格式，以及优化的人工粘性(滤波)格式，这里就不再一一介绍了，方程也不再解了。

对流方程

这里就展示一下之前的作业。
题目如下

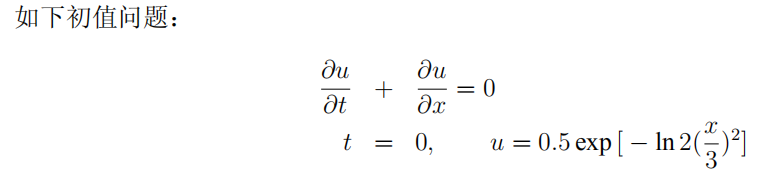
计算无量纲时间为400时的波形
$\Delta x=\Delta t=0.2$
使用十一点九阶DRP格式，以及优化过的人工粘性和优化的四步三阶R-K方法推进。实线是计算结果，三角是解析结果。可以看到几乎没有任何耗散和色散。

而相同的时间空间步长，使空间用中心差分时间欧拉前差的方法计算结果如下

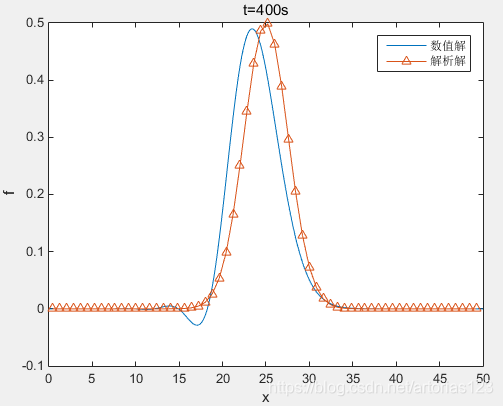
可以看到计算结果和解析解已经发生了明显的偏移，并且出现了不同波数分量的分离。

非线性方程

题目如下

t=18,36,72时的波形如下



可以看到当存在间断时DRP格式依然可以处理。