相机+机械臂组成的手眼系统,如同人的眼睛和手,眼睛看到东西后,让手能够准确的移动到物体的位置并抓取。相机所能看到的图像是2D屏幕,而手的移动是在3D空间中,因此手眼系统的功能就是能够将相机所拍摄到的2D画面,转换为手所在的3D空间的坐标。
常见的手眼系统有两种安装形式:

图a)的安装方式,相机安装在机械臂上,称之为眼在手上(eye in hand);图b)的安装方式,相机固定在机械臂之外的安装架上,称之为眼在手外(eye to hand)。
无论是眼在手上还是眼在手外,本质上都是将相机图像中的像素坐标系,转换到机械臂所在的空间坐标系中,手眼系统标定的意义就是找到从相机画面的像素坐标系转换到机械臂所在的三维空间的机械臂坐标系的变换过程,从而实现通过像素坐标以及到目标的距离可以准确的求解目标在机械臂坐标空间的三维坐标。
其中转换过程可以分为相机部分和机械臂部分,相机部分包含
- 像素坐标系
- 图像坐标系
- 相机坐标系
机械臂部分包含
- 基座坐标系
- 末端坐标系
- 夹具/工具坐标系
由于相机部分的坐标转换具备相同的规律和方法,而机械臂坐标根据使用夹具/工具的不同可能会有不同的结果,因此,我们在做手眼标定时,往往标定的是相机到机械臂末端(法兰盘)的变换关系,机械臂末端的坐标是可以直接读取并且保证精度。我们接下来描述的机器人坐标都认为是机械臂末端法兰盘的坐标,机械臂基座坐标系、工具坐标系转换的这一部分通常由机器人集成商来完成,对于视觉应用我们先不讨论机器人坐标部分,我们先只关注相机部分。
所以,我们先来分析手眼系统中相机相关的坐标系概念与转换关系。
相机模型
在讨论坐标系之前,我们先来了解一下相机模型。手眼系统的眼完成将二维平面(单位像素)映射到三维世界中的坐标点(单位为米),这个过程可以用一个相机模型来描述:
相机模型通常分为两类,一类是针孔模型,一类是鱼眼模型。
针孔模型:也叫小孔成像模型,是基于相机透镜畸变较小的情况下,物体的反射光经过透镜折射到图像传感器上,物和像之间的位置关系满足相似三角形的关系,即物体表面的坐标点和图像坐标点经过透镜后坐标之间为线性关系。
鱼眼模型:鱼眼镜头通常由多个不同的透镜组成,入射光经过多次折射投影到图像传感器上,鱼眼镜头因此可以获得更大范围的视角。因为多透镜的组合,鱼眼成像模型较为复杂,但是可以近似为单位球面的投影模型。
相机相关的坐标系
工业相机通常畸变程度较小,我们可以用针孔模型来计算,因此,按照针孔模型的小孔成像原理,手眼系统所涉及的相机各个坐标系表示如下图:

图中涉及到以下四个坐标系
uv:像素坐标系,原点为图像左上角,单位pixel
o-xy:图像坐标系,基于相机中感光元器件的现实平面空间,原点为成像平面中点,单位mm
Oc-XcYcZc:相机坐标系,光心为原点,单位m
Or-XrYrZr: 机器人坐标系,描述机械臂移动的位置,单位m
P:机器人坐标系中的一点,表示识别目标在机械臂三维空间中的位置
p:点p在图像中的成像点,在图像坐标系中的坐标为(x,y),在像素坐标系中的坐标为(u,v)
注:以下讨论的所有坐标系满足笛卡尔坐标系右手法则。
像素坐标系转换为图像坐标系

其中,O-uv是像素坐标系,O-xy是图像坐标系,要完成从pixel量纲到mm量纲的转换,就需要知道xy方向的像素尺寸dx和dy,单位mm,表示一个像素点的在传感器上的实际尺寸大小。设图像分辨率为1280x960,传感器尺寸为32mmx24mm,转换关系:
d
x
=
32
m
m
/
1280
d_x = 32mm / 1280
dx=32mm/1280
d
y
=
24
m
m
/
960
d_y = 24mm / 960
dy=24mm/960
x
=
(
u
−
640
)
d
x
=
u
d
x
−
640
d
x
=
u
d
x
−
u
0
d
x
x = (u - 640)d_x = ud_x - 640d_x = udx - u_0d_x
x=(u−640)dx=udx−640dx=udx−u0dx
y
=
(
v
−
480
)
d
y
=
v
d
y
−
480
d
y
=
v
d
y
−
v
0
d
y
y = (v - 480)d_y = vd_y - 480d_y = vd_y - v_0d_y
y=(v−480)dy=vdy−480dy=vdy−v0dy
其中u_0和v_0为像素坐标系到图像坐标系的平移分量。
矩阵运算形式:
[
x
y
1
]
=
[
d
x
0
−
u
0
d
x
0
d
y
−
v
0
d
y
0
0
1
]
[
u
v
1
]
\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] = \left[ \begin{matrix} d_x && 0 && -u_0d_x \\0 && d_y && -v_0d_y \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right]
⎣⎡xy1⎦⎤=⎣⎡dx000dy0−u0dx−v0dy1⎦⎤⎣⎡uv1⎦⎤
图像坐标系转换为相机坐标系

点p是图像坐标系上的一点,P是相机坐标系上的一点,f是相机焦距,O到Oc也就是传感器到光心的距离。由相似三角形可以计算:
X
c
x
=
Z
c
f
=
Y
c
y
\frac {Xc}{x} = \frac {Zc}{f} = \frac {Yc}{y}
xXc=fZc=yYc
转换关系:
X
c
=
Z
c
f
×
x
Xc = \frac {Zc}{f} \times x
Xc=fZc×x
Y
c
=
Z
c
f
×
y
Yc = \frac {Zc}{f} \times y
Yc=fZc×y
矩阵运算形式:
[
x
c
y
c
z
c
]
=
z
c
[
1
f
0
0
0
1
f
0
0
0
1
]
[
x
y
1
]
=
z
c
[
1
f
0
0
0
1
f
0
0
0
1
]
[
d
x
0
−
u
0
d
x
0
d
y
−
v
0
d
y
0
0
1
]
[
u
v
1
]
\left[ \begin{matrix} x_c\\y_c\\z_c \end{matrix} \right] = z_c \left[ \begin{matrix} \frac{1}{f} && 0 && 0 \\0 && \frac{1}{f} && 0 \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} x\\y\\1 \end{matrix} \right] = z_c \left[ \begin{matrix} \frac{1}{f} && 0 && 0 \\0 && \frac{1}{f} && 0 \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} d_x && 0 && -u_0d_x \\0 && d_y && -v_0d_y \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right]
⎣⎡xcyczc⎦⎤=zc⎣⎡f1000f10001⎦⎤⎣⎡xy1⎦⎤=zc⎣⎡f1000f10001⎦⎤⎣⎡dx000dy0−u0dx−v0dy1⎦⎤⎣⎡uv1⎦⎤
Zc表示相机距离目标的距离,可以通过3D相机直接获取,因此可以转换为二维平面上的坐标计算。
相机坐标系转换为机器人坐标系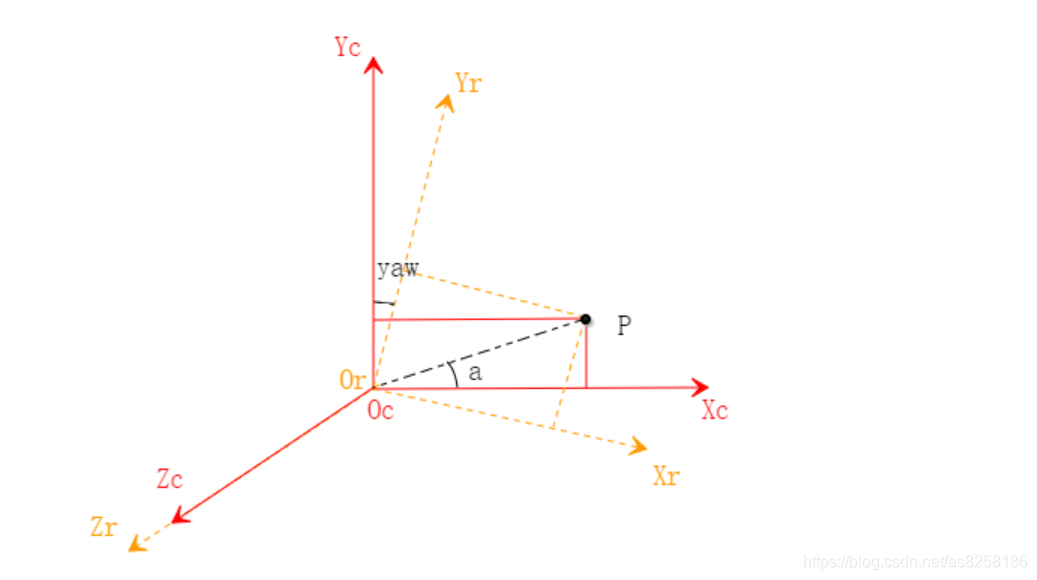
O_r-X_rY_rZ_r是机器人坐标系
O_c-X_cY_cZ_c是相机坐标系
P点在相机坐标系下的坐标为:(x_c,y_c,z_c),和x轴夹角为a,到原点的距离为R
假定机器人坐标系和相机坐标系Z轴重合,机器人坐标系绕着Z轴旋转一定的角度yaw
P点在机器人坐标系下(x_r,y_r,z_r)的坐标计算:
x r = R × cos ( a + y a w ) = R × c o s a × cos ( y a w ) − R × s i n a × s i n ( y a w ) x_r = R \times \cos(a+yaw) = R \times cosa \times \cos(yaw) - R \times sina \times sin(yaw) xr=R×cos(a+yaw)=R×cosa×cos(yaw)−R×sina×sin(yaw)
y r = R × sin ( a + y a w ) = R × s i n a × cos ( y a w ) + R × c o s a × s i n ( y a w ) y_r = R \times \sin(a+yaw) = R \times sina \times \cos(yaw) + R \times cosa \times sin(yaw) yr=R×sin(a+yaw)=R×sina×cos(yaw)+R×cosa×sin(yaw)
x c = R × c o s a x_c = R \times cosa xc=R×cosa
y
c
=
R
×
s
i
n
a
y_c = R \times sina
yc=R×sina
于是有:
x r = x c × cos ( y a w ) − y c × sin ( y a w ) x_r = x_c \times \cos(yaw) - y_c \times \sin(yaw) xr=xc×cos(yaw)−yc×sin(yaw)
y r = x c × sin ( y a w ) + y c × cos ( y a w ) y_r = x_c \times \sin(yaw) + y_c \times \cos(yaw) yr=xc×sin(yaw)+yc×cos(yaw)
z r = z c z_r = z_c zr=zc
转换为矩阵形式:
[
x
r
y
r
z
r
]
=
[
cos
(
y
a
w
)
−
sin
(
y
a
w
)
0
sin
(
y
a
w
)
cos
(
y
a
w
)
0
0
0
1
]
[
x
c
y
c
z
c
]
\left[ \begin{matrix} x_r\\y_r\\z_r \end{matrix} \right] = \left[ \begin{matrix} \cos(yaw) && -\sin(yaw) && 0 \\\sin(yaw) && \cos(yaw) && 0 \\0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} x_c\\y_c\\zc \end{matrix} \right]
⎣⎡xryrzr⎦⎤=⎣⎡cos(yaw)sin(yaw)0−sin(yaw)cos(yaw)0001⎦⎤⎣⎡xcyczc⎦⎤
其中
[
cos
(
y
a
w
)
−
sin
(
y
a
w
)
0
sin
(
y
a
w
)
cos
(
y
a
w
)
0
0
0
1
]
就
是
所
谓
的
绕
Z
轴
旋
转
a
角
度
的
旋
转
矩
阵
R
z
−
1
\left[ \begin{matrix} \cos(yaw) && -\sin(yaw) && 0 \\\sin(yaw) && \cos(yaw) && 0 \\0 && 0 && 1 \end{matrix} \right]就是所谓的绕Z轴旋转a角度的旋转矩阵R_z^{-1}
⎣⎡cos(yaw)sin(yaw)0−sin(yaw)cos(yaw)0001⎦⎤就是所谓的绕Z轴旋转a角度的旋转矩阵Rz−1
注 : 之 所 以 是 R z − 1 表 示 , 是 因 为 诸 如 o p e n c v 的 函 数 以 及 学 术 论 文 讨 论 , 都 是 以 机 器 人 坐 标 系 到 像 素 坐 标 系 的 旋 转 矩 阵 作 为 R , 这 里 我 们 是 以 像 素 坐 标 系 到 机 器 人 坐 标 系 变 换 来 讨 论 , 因 此 用 逆 矩 阵 R z − 1 来 表 示 注:之所以是R_z^{-1}表示,是因为诸如opencv的函数以及学术论文讨论,都是以机器人坐标系到像素坐标系的旋转矩阵作为R,这里我们是以像素坐标系到机器人坐标系变换来讨论,因此用逆矩阵 R_z^{-1} 来表示 注:之所以是Rz−1表示,是因为诸如opencv的函数以及学术论文讨论,都是以机器人坐标系到像素坐标系的旋转矩阵作为R,这里我们是以像素坐标系到机器人坐标系变换来讨论,因此用逆矩阵Rz−1来表示
同理可得,绕着X轴旋转roll的旋转矩阵为:
R
x
−
1
=
[
1
0
0
0
cos
(
r
o
l
l
)
−
sin
(
r
o
l
l
)
0
sin
(
r
o
l
l
)
cos
(
r
o
l
l
)
]
R_x^{-1} = \left[ \begin{matrix} 1 && 0 && 0 \\0 && \cos(roll) && -\sin(roll) \\0 && \sin(roll) && \cos(roll) \end{matrix} \right]
Rx−1=⎣⎡1000cos(roll)sin(roll)0−sin(roll)cos(roll)⎦⎤
绕着Y轴旋转pitch的旋转矩阵为:
R
y
−
1
=
[
cos
(
p
i
t
c
h
)
0
sin
(
p
i
t
c
h
)
0
1
0
−
sin
(
p
i
t
c
h
)
0
cos
(
p
i
t
c
h
)
]
R_y^{-1} = \left[ \begin{matrix} \cos(pitch) && 0 && \sin(pitch) \\0 && 1 && 0 \\-\sin(pitch) && 0 && \cos(pitch) \end{matrix} \right]
Ry−1=⎣⎡cos(pitch)0−sin(pitch)010sin(pitch)0cos(pitch)⎦⎤
当三个坐标轴都有旋转时,旋转矩阵:
R
−
1
=
R
z
−
1
R
y
−
1
R
x
−
1
=
[
cos
(
y
a
w
)
cos
(
p
i
t
c
h
)
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
−
sin
(
y
a
w
)
cos
(
r
o
l
l
)
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
c
o
s
(
r
o
l
l
)
+
sin
(
y
a
w
)
sin
(
r
o
l
l
)
sin
(
y
a
w
)
cos
(
p
i
t
c
h
)
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
+
cos
(
y
a
w
)
cos
(
r
o
l
l
)
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
−
cos
(
y
a
w
)
sin
(
r
o
l
l
)
−
sin
(
p
i
t
c
h
)
cos
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
cos
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
]
R^{-1} = R_z^{-1}R_y^{-1}R_x^{-1} = \left[ \begin{matrix} \cos(yaw)\cos(pitch) && \cos(yaw)\sin(pitch)\sin(roll) - \sin(yaw)\cos(roll) && \cos(yaw)\sin(pitch)cos(roll) + \sin(yaw)\sin(roll) \\\sin(yaw)\cos(pitch) && \sin(yaw)\sin(pitch)\sin(roll) + \cos(yaw)\cos(roll) && \sin(yaw)\sin(pitch)\cos(roll)-\cos(yaw)\sin(roll) \\-\sin(pitch) && \cos(pitch)\sin(roll) && \cos(pitch)\cos(roll) \end{matrix} \right]
R−1=Rz−1Ry−1Rx−1=⎣⎡cos(yaw)cos(pitch)sin(yaw)cos(pitch)−sin(pitch)cos(yaw)sin(pitch)sin(roll)−sin(yaw)cos(roll)sin(yaw)sin(pitch)sin(roll)+cos(yaw)cos(roll)cos(pitch)sin(roll)cos(yaw)sin(pitch)cos(roll)+sin(yaw)sin(roll)sin(yaw)sin(pitch)cos(roll)−cos(yaw)sin(roll)cos(pitch)cos(roll)⎦⎤
如果考虑平移,在X,Y,Z分量上加上一个固定的平移数值
[
Δ
x
Δ
y
Δ
z
]
,
构
成
3
×
1
\left[ \begin{matrix} \Delta x\\\Delta y\\\Delta z \end{matrix} \right],构成3 \times 1
⎣⎡ΔxΔyΔz⎦⎤,构成3×1
的平移矩阵-T
注:这里用-T表示是为了和Opencv的输出的tvecs区分,opencv输出平移矩阵是从机器人坐标系到像素坐标系,记为T。我们计算从像素坐标系到机器人坐标系时取反运算即可,记为-T
即:
[
x
r
y
r
z
r
]
=
R
−
1
(
[
x
c
y
c
z
c
]
−
T
)
\left[ \begin{matrix} x_r\\y_r\\z_r \end{matrix} \right] = R^{-1}( \left[ \begin{matrix} x_c\\y_c\\z_c \end{matrix} \right] - T)
⎣⎡xryrzr⎦⎤=R−1(⎣⎡xcyczc⎦⎤−T)
最终变换
把以上所有的公式合并起来,得到像素坐标到机器人坐标的变换公式:
[
x
r
y
r
z
r
]
=
R
−
1
(
z
c
×
[
1
f
0
0
0
1
f
0
0
0
1
]
[
d
x
0
−
u
0
d
x
0
d
y
−
v
0
d
y
0
0
1
]
[
u
v
1
]
−
T
)
\left[ \begin{matrix} x_r\\y_r\\z_r \end{matrix} \right] = R^{-1}(z_c \times \left[ \begin{matrix} \frac{1}{f} && 0 && 0 \\0 && \frac{1}{f} && 0 \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} d_x && 0 && -u_0d_x \\0 && d_y && -v_0d_y \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] - T)
⎣⎡xryrzr⎦⎤=R−1(zc×⎣⎡f1000f10001⎦⎤⎣⎡dx000dy0−u0dx−v0dy1⎦⎤⎣⎡uv1⎦⎤−T)
根据矩阵结合律运算结合中间两个矩阵:
[
x
r
y
r
z
r
]
=
R
−
1
(
z
c
×
[
d
x
f
0
−
u
0
d
x
f
0
d
y
f
−
v
0
d
y
f
0
0
1
]
[
u
v
1
]
−
T
)
\left[ \begin{matrix} x_r\\y_r\\z_r \end{matrix} \right] = R^{-1}(z_c \times \left[ \begin{matrix} \frac{d_x}{f} && 0 && -\frac{u_0d_x}{f} \\0 && \frac{d_y}{f} && -\frac{v_0d_y}{f} \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] - T)
⎣⎡xryrzr⎦⎤=R−1(zc×⎣⎢⎡fdx000fdy0−fu0dx−fv0dy1⎦⎥⎤⎣⎡uv1⎦⎤−T)
通
常
我
们
用
f
x
=
d
x
f
表
示
通常我们用f_x = \frac {d_x}{f}表示
通常我们用fx=fdx表示
[
x
r
y
r
z
r
]
=
R
−
1
(
z
c
×
[
1
f
x
0
−
u
0
f
x
0
1
f
y
−
v
0
f
y
0
0
1
]
[
u
v
1
]
−
T
)
\left[ \begin{matrix} x_r\\y_r\\z_r \end{matrix} \right] = R^{-1}( z_c \times \left[ \begin{matrix} \frac{1}{f_x} && 0 && -\frac{u_0}{f_x} \\0 && \frac{1}{f_y} && -\frac{v_0}{f_y} \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] - T)
⎣⎡xryrzr⎦⎤=R−1(zc×⎣⎡fx1000fy10−fxu0−fyv01⎦⎤⎣⎡uv1⎦⎤−T)
右边从左往右第一个是相机的外参矩阵的逆矩阵,第二个是相机的内参矩阵的逆矩阵(为什么是逆矩阵,因为opencv的函数计算的关系,下面会讲)
如果对矩阵不好理解,我们展开为线性方程:
x
r
=
cos
(
y
a
w
)
cos
(
p
i
t
c
h
)
×
(
z
c
×
u
−
u
0
f
x
−
Δ
x
)
+
(
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
−
sin
(
y
a
w
)
cos
(
r
o
l
l
)
)
×
(
z
c
×
v
−
v
0
f
y
−
Δ
y
)
+
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
c
o
s
(
r
o
l
l
)
+
sin
(
y
a
w
)
sin
(
r
o
l
l
)
×
(
z
c
−
Δ
z
)
x_r = \cos(yaw)\cos(pitch) \times (z_c \times \frac {u - u_0}{f_x} - \Delta x) + (\cos(yaw)\sin(pitch)\sin(roll) - \sin(yaw)\cos(roll)) \times (z_c \times \frac {v - v_0}{f_y} -\Delta y) + \cos(yaw)\sin(pitch)cos(roll) + \sin(yaw)\sin(roll) \times (z_c - \Delta z)
xr=cos(yaw)cos(pitch)×(zc×fxu−u0−Δx)+(cos(yaw)sin(pitch)sin(roll)−sin(yaw)cos(roll))×(zc×fyv−v0−Δy)+cos(yaw)sin(pitch)cos(roll)+sin(yaw)sin(roll)×(zc−Δz)
y
r
=
sin
(
y
a
w
)
cos
(
p
i
t
c
h
)
×
(
z
c
×
u
−
u
0
f
x
−
Δ
x
)
+
(
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
+
cos
(
y
a
w
)
cos
(
r
o
l
l
)
)
×
(
z
c
×
v
−
v
0
f
y
−
Δ
y
)
+
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
−
cos
(
y
a
w
)
sin
(
r
o
l
l
)
×
(
z
c
−
Δ
z
)
y_r = \sin(yaw)\cos(pitch) \times (z_c \times \frac {u - u_0}{f_x} - \Delta x) + (\sin(yaw)\sin(pitch)\sin(roll) + \cos(yaw)\cos(roll)) \times (z_c \times \frac {v - v_0}{f_y} - \Delta y) + \sin(yaw)\sin(pitch)\cos(roll)-\cos(yaw)\sin(roll) \times (z_c - \Delta z)
yr=sin(yaw)cos(pitch)×(zc×fxu−u0−Δx)+(sin(yaw)sin(pitch)sin(roll)+cos(yaw)cos(roll))×(zc×fyv−v0−Δy)+sin(yaw)sin(pitch)cos(roll)−cos(yaw)sin(roll)×(zc−Δz)
z
r
=
−
sin
(
p
i
t
c
h
)
×
(
z
c
×
u
−
u
0
f
x
−
Δ
x
)
+
cos
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
×
(
z
c
×
v
−
v
0
f
y
−
Δ
y
)
+
cos
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
×
(
z
c
−
Δ
z
)
z_r = -\sin(pitch) \times (z_c \times \frac {u - u_0}{f_x} - \Delta x)+ \cos(pitch)\sin(roll) \times (z_c \times \frac {v - v_0}{f_y} - \Delta y) + \cos(pitch)\cos(roll) \times (z_c - \Delta z)
zr=−sin(pitch)×(zc×fxu−u0−Δx)+cos(pitch)sin(roll)×(zc×fyv−v0−Δy)+cos(pitch)cos(roll)×(zc−Δz)
从
展
开
式
中
可
以
看
出
,
对
于
某
一
个
式
子
,
z
c
深
度
值
,
f
相
机
焦
距
,
d
x
、
d
y
像
素
尺
寸
,
u
0
、
v
0
像
素
坐
标
系
偏
移
量
都
是
已
知
的
从展开式中可以看出,对于某一个式子,z_c深度值,f相机焦距,d_x、d_y像素尺寸,u_0、v_0像素坐标系偏移量都是已知的
从展开式中可以看出,对于某一个式子,zc深度值,f相机焦距,dx、dy像素尺寸,u0、v0像素坐标系偏移量都是已知的
一共有 p i t c h 、 r o l l 、 y a w 、 Δ x 、 Δ y 、 Δ z pitch、roll、yaw、\Delta x、 \Delta y、 \Delta z pitch、roll、yaw、Δx、Δy、Δz六个未知量
根据n元一次方程的求解要求,必须提供6组以上的非线性解才能确定方程的唯一系数,因此,在求解过程中,至少需要机械臂移动6个非线性点,才能完全确定3D空间内像素坐标系到机器人坐标系的变换关系。如果是2D平面,相当于去掉yaw和z的偏移,有4个未知量的线性方程,则需要至少4个点。
其实到这里,根据以上理论编码求解方程就能够实现求解。由于上述方程比较复杂,求解不是简单的事情,对于工程师来说没有必要把理论实践一遍,opencv已经给我们提供了封装好的接口,我们可以基于封装好的轮子快速得到我们需要的结果。
上面我们分析的是从像素坐标到机器人坐标的转换,但是在opencv提供的方法往往是按照机器人坐标(世界坐标系)到像素坐标转换的公式计算,得到的矩阵如下,
Z
c
[
u
v
1
]
=
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
[
f
0
0
0
0
f
0
0
0
0
1
0
]
[
R
T
0
1
]
[
x
r
y
r
z
r
1
]
=
[
f
x
0
u
0
0
0
f
y
v
0
0
0
0
1
0
]
[
R
T
0
1
]
[
x
r
y
r
z
r
1
]
Z_c \left[ \begin{matrix} u\\ v\\ 1 \end{matrix} \right] = \left[ \begin{matrix} \frac 1 {d_x} && 0 && u_0\\ 0 && \frac 1 {d_y} && v_0\\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} f && 0 && 0 && 0\\ 0 && f && 0 && 0\\ 0 && 0 && 1 && 0 \end{matrix} \right] \left[ \begin{matrix} R && T\\ 0 && 1 \end{matrix} \right] \left[ \begin{matrix} x_r\\ y_r\\ z_r\\ 1 \end{matrix} \right] = \left[ \begin{matrix} f_x && 0 && u_0 && 0\\ 0 && f_y && v_0 && 0\\ 0 && 0 && 1 && 0 \end{matrix} \right] \left[ \begin{matrix} R && T\\ 0 && 1 \end{matrix} \right] \left[ \begin{matrix} x_r\\ y_r\\ z_r\\ 1 \end{matrix} \right]
Zc⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡f000f0001000⎦⎤[R0T1]⎣⎢⎢⎡xryrzr1⎦⎥⎥⎤=⎣⎡fx000fy0u0v01000⎦⎤[R0T1]⎣⎢⎢⎡xryrzr1⎦⎥⎥⎤
其
中
[
f
x
0
u
0
0
0
f
y
v
0
0
0
0
1
0
]
为
相
机
内
参
其中\left[ \begin{matrix} f_x && 0 && u_0 && 0\\ 0 && f_y && v_0 && 0\\ 0 && 0 && 1 && 0 \end{matrix} \right]为相机内参
其中⎣⎡fx000fy0u0v01000⎦⎤为相机内参
[ R T 0 1 ] 为 相 机 外 参 \left[ \begin{matrix} R && T\\ 0 && 1 \end{matrix} \right] 为相机外参 [R0T1]为相机外参
注:opencv外参求解cvFindExtrinsicCameraParams2源码:
返回的旋转矩阵的结果是按照从世界坐标到像素坐标的映射关系计算的。
因此当我们使用opencv得到内参和外参矩阵时,还需要求解它的逆矩阵,才能通过像素坐标转换为机器人坐标。从上述分析已经知道了内参矩阵的逆矩阵,而至于外参矩阵,由于其本身是一个正交矩阵,所以,转置矩阵也是他的逆矩阵,我们只需要把opencv计算得到的外参矩阵转置即可,感兴趣的小伙伴可以自己去验证一下。
R
=
R
−
1
T
=
[
cos
(
y
a
w
)
cos
(
p
i
t
c
h
)
sin
(
y
a
w
)
cos
(
p
i
t
c
h
)
−
sin
(
p
i
t
c
h
)
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
−
sin
(
y
a
w
)
cos
(
r
o
l
l
)
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
+
cos
(
y
a
w
)
cos
(
r
o
l
l
)
cos
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
c
o
s
(
r
o
l
l
)
+
sin
(
y
a
w
)
sin
(
r
o
l
l
)
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
−
cos
(
y
a
w
)
sin
(
r
o
l
l
)
cos
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
]
R = {R^{-1}}^T = \left[ \begin{matrix} \cos(yaw)\cos(pitch) && \sin(yaw)\cos(pitch) && -\sin(pitch) \\ \cos(yaw)\sin(pitch)\sin(roll) - \sin(yaw)\cos(roll) && \sin(yaw)\sin(pitch)\sin(roll) + \cos(yaw)\cos(roll) && \cos(pitch)\sin(roll) \\ \cos(yaw)\sin(pitch)cos(roll) + \sin(yaw)\sin(roll) && \sin(yaw)\sin(pitch)\cos(roll)-\cos(yaw)\sin(roll) && \cos(pitch)\cos(roll) \end{matrix} \right]
R=R−1T=⎣⎡cos(yaw)cos(pitch)cos(yaw)sin(pitch)sin(roll)−sin(yaw)cos(roll)cos(yaw)sin(pitch)cos(roll)+sin(yaw)sin(roll)sin(yaw)cos(pitch)sin(yaw)sin(pitch)sin(roll)+cos(yaw)cos(roll)sin(yaw)sin(pitch)cos(roll)−cos(yaw)sin(roll)−sin(pitch)cos(pitch)sin(roll)cos(pitch)cos(roll)⎦⎤
注:以上得到的结果是按照x-roll,y-pitch,z-yaw来计算的,如果坐标系位置和定义关系不同,只需要把角度替换即可。如,上述我们定义绕y轴转是pitch,绕z转是yaw,如果你自己的坐标系定义是绕y转是yaw,绕x轴转是pitch,绕z轴旋转是roll,那么矩阵的[0][0]元素相应的变为cos(yaw)cos(roll),也就是矩阵的第一个元素是绕y轴旋转和绕z轴旋转角度的三角函数乘积,这一点是不变的。
相机畸变
前面分析的坐标变换都是没有考虑畸变的,各个坐标系之间满足线性变换,但实际上,相机镜头由于镜面曲率的关系导致放大率并一定是均匀的,所以相机在成像过程中会存在一定的畸变,相机的畸变通常分为两类:
- 径向畸变,通常因为镜头表面曲率不同产生的畸变,这种畸变是对称的。径向畸变根据放大率的不同又分为两类:
- 枕形畸变,视野中边缘区域的放大率远大于中心区域的放大率,常见于远摄摄像头(下图左)
- 桶形畸变,视野中中心区域的放大率远大于边缘区域的放大率,常见于广角摄像头和鱼眼摄像头(下图右)
- 切向畸变,通常是因为相机装配过程,透镜平面和CCD/CMOS传感器平面没有平行,这种畸变不对称,在图像区域表现为单侧畸变,类似透视畸变。

在工业相机中,比较常见的畸变类型为桶形畸变和切向畸变。
桶形畸变矫正
根据前面讨论,我们把手眼系统的相机坐标系看做小孔成像模型,认为他们坐标系之间满足线性变换的关系。但是由于畸变的存在,从相机坐标系到图像坐标系之间不满足线性关系,因此为了能够应用小孔成像模型对坐标系之间进行线性变换的计算,我们需要对相机成像后的图像坐标进行畸变矫正。
矫正的计算公式可以简化为(推导过程不赘述,感兴趣的可以自行查阅资料):
x d i s t o r t = x c o r r e c t 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 1 + k 4 r 2 + k 5 r 4 + k 6 r 6 x_{distort} = x_{correct}\frac {1 + k_1r^2 + k_2r^4 + k_3r^6}{1 + k_4r^2 + k_5r^4 + k_6r^6} xdistort=xcorrect1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6
y d i s t o r t = y c o r r e c t 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 1 + k 4 r 2 + k 5 r 4 + k 6 r 6 y_{distort} = y_{correct}\frac {1 + k_1r^2 + k_2r^4 + k_3r^6}{1 + k_4r^2 + k_5r^4 + k_6r^6} ydistort=ycorrect1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6
其 中 ( x d i s t o r t , y d i s t o r t ) 表 示 在 原 图 像 上 的 图 像 坐 标 , 不 是 像 素 坐 标 , 是 带 畸 变 的 其中(x_{distort},y_{distort})表示在原图像上的图像坐标,不是像素坐标,是带畸变的 其中(xdistort,ydistort)表示在原图像上的图像坐标,不是像素坐标,是带畸变的。
( x c o r r e c t , y c o r r e c t ) 表 示 畸 变 矫 正 后 的 图 像 坐 标 。 r 表 示 该 点 坐 标 到 原 点 的 距 离 (x_{correct},y_{correct})表示畸变矫正后的图像坐标。r表示该点坐标到原点的距离 (xcorrect,ycorrect)表示畸变矫正后的图像坐标。r表示该点坐标到原点的距离
k 1 , k 2 , k 3 , k 4 , k 5 , k 6 为 径 向 畸 变 系 数 k_1,k_2,k_3,k_4,k_5,k_6为径向畸变系数 k1,k2,k3,k4,k5,k6为径向畸变系数
切向畸变矫正
切向畸变计算公式
x d i s t o r t = x c o r r e c t + [ 2 p 1 x c o r r e c t y c o r r e c t + p 2 ( r 2 + 2 x c o r r e c t 2 ) ] x_{distort} = x_{correct} + [2p_1x_{correct}y_{correct} + p_2(r^2 + 2 x_{correct}^2)] xdistort=xcorrect+[2p1xcorrectycorrect+p2(r2+2xcorrect2)]
y d i s t o r t = y c o r r e c t + [ 2 p 2 x c o r r e c t y c o r r e c t + p 1 ( r 2 + 2 y c o r r e c t 2 ) ] y_{distort} = y_{correct} + [2p_2 x_{correct}y_{correct} + p_1(r^2 + 2y_{correct}^2)] ydistort=ycorrect+[2p2xcorrectycorrect+p1(r2+2ycorrect2)]
总的畸变矫正公式为:
x
d
i
s
t
o
r
t
=
x
c
o
r
r
e
c
t
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
1
+
k
4
r
2
+
k
5
r
4
+
k
6
r
6
+
[
2
p
1
x
c
o
r
r
e
c
t
y
c
o
r
r
e
c
t
+
p
2
(
r
2
+
2
x
c
o
r
r
e
c
t
2
)
]
x_{distort} = x_{correct}\frac {1 + k_1r^2 + k_2r^4 + k_3r^6}{1 + k_4r^2 + k_5r^4 + k_6r^6} + [2p_1x_{correct}y_{correct} + p_2(r^2 + 2 x_{correct}^2)]
xdistort=xcorrect1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6+[2p1xcorrectycorrect+p2(r2+2xcorrect2)]
y d i s t o r t = y c o r r e c t 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 1 + k 4 r 2 + k 5 r 4 + k 6 r 6 + [ 2 p 2 x c o r r e c t y c o r r e c t + p 1 ( r 2 + 2 y c o r r e c t 2 ) ] y_{distort} = y_{correct}\frac {1 + k_1r^2 + k_2r^4 + k_3r^6}{1 + k_4r^2 + k_5r^4 + k_6r^6} + [2p_2 x_{correct}y_{correct} + p_1(r^2 + 2y_{correct}^2)] ydistort=ycorrect1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6+[2p2xcorrectycorrect+p1(r2+2ycorrect2)]
把畸变考虑进来,和前面线性变换的公式组合起来,一个相机系统从像素坐标到机器人的坐标变换过程
-
畸变像素坐标->畸变图像坐标
(u,v)畸变像素坐标,内参矩阵
-
畸变图像坐标->无畸变图像坐标
畸变系数
-
无畸变图像坐标->相机坐标
Zc相机到目标的高度
-
相机坐标->机器人坐标
旋转平移矩阵RT
把畸变计算公式和坐标系变换公式合并:
x
r
=
cos
(
y
a
w
)
cos
(
p
i
t
c
h
)
×
(
z
c
×
x
c
o
r
r
e
c
t
−
Δ
x
)
+
(
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
−
sin
(
y
a
w
)
cos
(
r
o
l
l
)
)
×
(
z
c
×
y
c
o
r
r
e
c
t
−
Δ
y
)
+
cos
(
y
a
w
)
sin
(
p
i
t
c
h
)
c
o
s
(
r
o
l
l
)
+
sin
(
y
a
w
)
sin
(
r
o
l
l
)
×
(
z
c
−
Δ
z
)
x_r = \cos(yaw)\cos(pitch) \times (z_c \times x_{correct} - \Delta x) + (\cos(yaw)\sin(pitch)\sin(roll) - \sin(yaw)\cos(roll)) \times (z_c \times y_{correct} -\Delta y) + \cos(yaw)\sin(pitch)cos(roll) + \sin(yaw)\sin(roll) \times (z_c - \Delta z)
xr=cos(yaw)cos(pitch)×(zc×xcorrect−Δx)+(cos(yaw)sin(pitch)sin(roll)−sin(yaw)cos(roll))×(zc×ycorrect−Δy)+cos(yaw)sin(pitch)cos(roll)+sin(yaw)sin(roll)×(zc−Δz)
y
r
=
sin
(
y
a
w
)
cos
(
p
i
t
c
h
)
×
(
z
c
×
x
c
o
r
r
e
c
t
−
Δ
x
)
+
(
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
sin
(
r
o
l
l
)
+
cos
(
y
a
w
)
cos
(
r
o
l
l
)
)
×
(
z
c
×
y
c
o
r
r
e
c
t
−
Δ
y
)
+
sin
(
y
a
w
)
sin
(
p
i
t
c
h
)
cos
(
r
o
l
l
)
−
cos
(
y
a
w
)
sin
(
r
o
l
l
)
×
(
z
c
−
Δ
z
)
y_r = \sin(yaw)\cos(pitch) \times (z_c \times x_{correct} - \Delta x) + (\sin(yaw)\sin(pitch)\sin(roll) + \cos(yaw)\cos(roll)) \times (z_c \times y_{correct} - \Delta y) + \sin(yaw)\sin(pitch)\cos(roll)-\cos(yaw)\sin(roll) \times (z_c - \Delta z)
yr=sin(yaw)cos(pitch)×(zc×xcorrect−Δx)+(sin(yaw)sin(pitch)sin(roll)+cos(yaw)cos(roll))×(zc×ycorrect−Δy)+sin(yaw)sin(pitch)cos(roll)−cos(yaw)sin(roll)×(zc−Δz)
z r = − sin ( p i t c h ) × ( z c × x c o r r e c t − Δ x ) + cos ( p i t c h ) sin ( r o l l ) × ( z c × y c o r r e c t − Δ y ) + cos ( p i t c h ) cos ( r o l l ) × ( z c − Δ z ) z_r = -\sin(pitch) \times (z_c \times x_{correct} - \Delta x)+ \cos(pitch)\sin(roll) \times (z_c \times y_{correct} - \Delta y) + \cos(pitch)\cos(roll) \times (z_c - \Delta z) zr=−sin(pitch)×(zc×xcorrect−Δx)+cos(pitch)sin(roll)×(zc×ycorrect−Δy)+cos(pitch)cos(roll)×(zc−Δz)
[ x d i s t o r t y d i s t o r t 1 ] = [ 1 f x 0 − u 0 f x 0 1 f y − v 0 f y 0 0 1 ] [ u v 1 ] \left[\begin{matrix} x_{distort} \\ y_{distort} \\ 1\end{matrix} \right] = \left[ \begin{matrix} \frac{1}{f_x} && 0 && -\frac{u_0}{f_x} \\0 && \frac{1}{f_y} && -\frac{v_0}{f_y} \\ 0 && 0 && 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] ⎣⎡xdistortydistort1⎦⎤=⎣⎡fx1000fy10−fxu0−fyv01⎦⎤⎣⎡uv1⎦⎤
Final
到这里我们详细讲解了手眼系统的相机部分坐标变换过程,各个坐标系的理论计算,以及畸变矫正的理论计算,并且结合opencv初步展示了理论计算与实际工程如何去结合使用,通过计算我们了解到,在坐标系变换过程中产生了两个矩阵参数,分别是内参矩阵和外参矩阵,内参矩阵只与相机的内部构造和参数有关,外参矩阵只与相机、机械臂的安装位姿有关。
在手眼系统中计算求解相机内参、外参矩阵的过程我们称之为相机标定,当我们得到这两个矩阵参数时,就可以按照线性方程的格式通过像素坐标求解机械臂坐标。虽然说网上存在很多的资料推导讲解,当然,这都是理论部分,准备哪些已知量,如何准备,得到之后如何按照理论公式计算,这是工程应用中需要真正解决的问题。很多资料并没有系统的讲解这些问题,这让很多人在明白理论后仍然无法下手去实践应用手眼标定。所以后续会根据眼在手上、眼在手外这两种安装方式,讨论手眼标定的实践方式以及工程实现。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








