【论文笔记】Deep Neural Decision Forests

最新推荐文章于 2024-06-12 09:38:37 发布

asd8705

最新推荐文章于 2024-06-12 09:38:37 发布

阅读量1.7k

点赞数

原文地址：http://blog.csdn.net/elaine_bao/article/details/49894155

文章链接：ICCV2015 DEEP NEURAL DECISION FORESTS(from 微软)
what does this paper bring as about

The main contribution of our work relates to enriching decision trees with the capability of representation learning, which requires a tree training approach departing from the prevailing greedy, local optimization procedures typically employed in the literature。
随机森林可以被用作深度学习网络最后一层的分类器，通过前面的系统输出data representation,然后用随机森林作为分类器进行分类。并且，文章提到，通过将传统随机森林的local optimize改造成通过back propagation进行global optimize,随机森林的参数训练可以与前端的深度学习网络进行无缝衔接。

1. 决策树、回归树、随机森林

决策树：大多是用来分类的。选择分类属性的标准是信息增益最大（Information gain），涉及到熵这个概念（The Shannon entropy）。公式如下，h(s)表示node s的熵，信息增益则是node s的熵减去它的左右子节点的熵。如果信息增益为正，则说明这是一个好的分裂split。
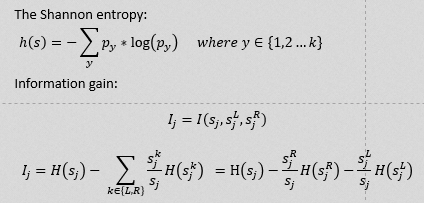
这里写图片描述
- 决策树的构造方法：从根节点开始，
1. N个M维的样本，那么共有（N-1）*M种splitting options可以将其分裂
2. 根据information gain的原则选择最大增益的splitting option进行分裂
3. 分裂到子节点后，重复1-3直至停止条件（停止条件一般包括Max depth, min info-gain, pure(节点已经分类纯净), max count of node）

回归树：顾名思义就是来做回归的，选择变量的标准用残差平方和。熟悉通常意义的回归分析的人，一定知道回归分析的最小二乘解就是最小化残差平方和的。在回归树的根部，所有的样本都在这里，此时树还没有生长，这棵树的残差平方和就是回归的残差平方和。然后选择一个变量也就是一个属性，通过它进行分类后的两部分的分别的残差平方和的和最小。然后在分叉的两个节点处，再利用这样的准则，选择之后的分类属性。一直这样下去，直到生成一颗完整的树。
随机森林：是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

2.“概率”决策树的构成

在传统的决策树中，分裂节点是二值的，即它决定了经过这个节点以后是向左分支走还是向右分支走，并且这个结果是一旦决定就不可更改的。这就导致网络有可能在当前node是最优的(根据info-gain的原则)但是最后的分类效果并不是最优的。因此本文考虑“概率”决策树，即每个node的分裂是一个概率：
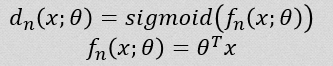
这里写图片描述
其中x为输入样本（图像的特征），theta为树的分裂参数
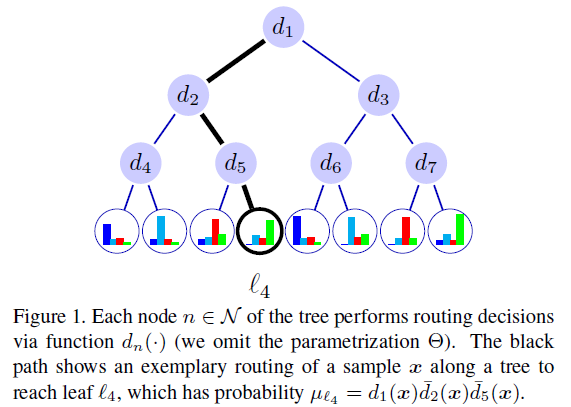
那么样本x到达某个leaf node的概率为routing function：

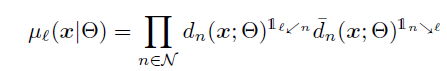
(N表示除leaf node以外的decision nodes)
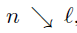
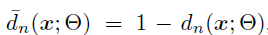
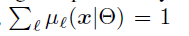
其中表示l属于当前node的左支成立，此时的概率为dn，表示l属于当前node的右支成立，此时概率这里写图片描述。我们知道。routing function的意思可以通过下图来解释：

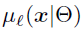
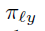
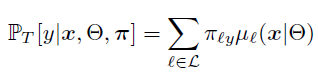
本文在最终的叶子节点中还增加了一个概率分布(leaf node distribution)，最终的分类结果=样本x到达某个叶子节点的概率( 这里写图片描述 )*某个叶子节点中某个类的概率()：
(大L表示所有leaf nodes)

3.“概率”决策树参数学习

从上述决策树的构成中我们知道，整个网络中有两个参数需要学习：leaf node distribution π和split param θ。
Loss function:
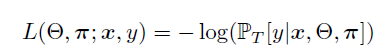
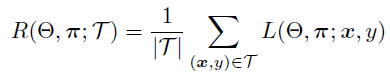
这里写图片描述

给定数据集T，Risk R就是（π，θ）的函数。
这种两个参数的学习通常采用类似于EM算法的方法进行迭代，首先固定π，对θ的学习采用随机梯度下降法（SGD），这和neural network中我们常做的back propagation是一样的,
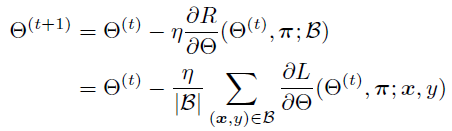
这里写图片描述
(B表示的是数据集T中一个随机的mini batch)
然后固定θ，优化π，文中最后证明优化π是一个凸优化的问题，它的求解是global的，因此在整个数据集上解下式：

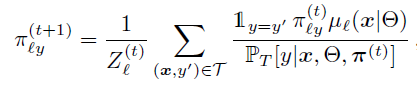
整体的求参过程就是以上两步不断迭代的过程：
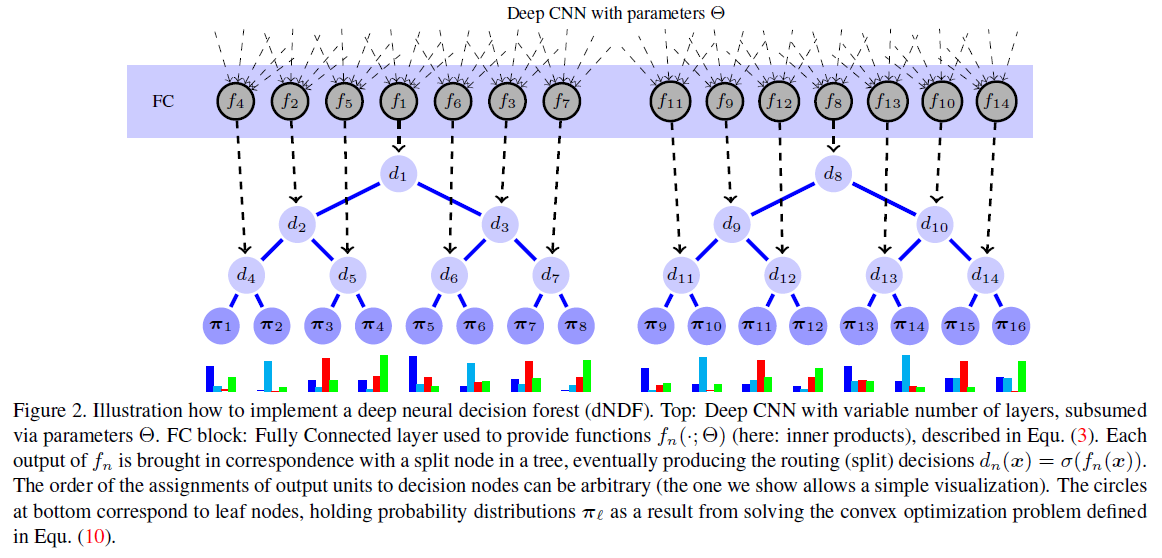
这里写图片描述