编程之美1.3 摞烙饼的排序

问题：

    星期五的晚上，一帮同事在希格玛大厦附近的“硬盘酒吧”多喝了几杯。程序员多喝了几杯之后谈什么呢？自然是算法问题。有个同事说：“我以前在餐馆打工，顾客经常点非常多的烙饼。店里的饼大小不一，我习惯在到达顾客饭桌前，把一摞饼按照大小次序摆好——小的在上面，大的在下面。由于我一只手托着盘子，只好用另一只手，一次抓住最上面的几块饼，把它们上下颠倒个个儿，反复几次之后，这摞烙饼就排好序了。我后来想，这实际上是个有趣的排序问题：假设有n块大小不一的烙饼，那最少要翻几次，才能达到最后大小有序的结果呢？”

你能否写出一个程序，对于n块大小不一的烙饼，输出最优化的翻饼过程呢？

 

（1）基本步骤

1、最上面的和下面“未选出的最大”的做一次翻转——————》最大的跑到上面了

2、最大的和下面未初始化的第一个翻转——————》最大的跑到了最下面

3、重复以上过程，直到全部有序

 

（2）如何改进以上的次数？

 

关于一摞烙饼的排序问题我们可以采用递归的方式来完成。其间我们要做的是尽量调整UpperBound和LowerBound，已减少运算次数。对于这种方法，在算法课中我们应该称之为：Tree Searching Strategy。即整个解空间为一棵搜索树，我们按照一定的策略遍历解空间，并寻找最优解。一旦找到比当前最优解更好的解，就用它替换当前最优解，并用它来进行“剪枝”操作来加速求解过程。

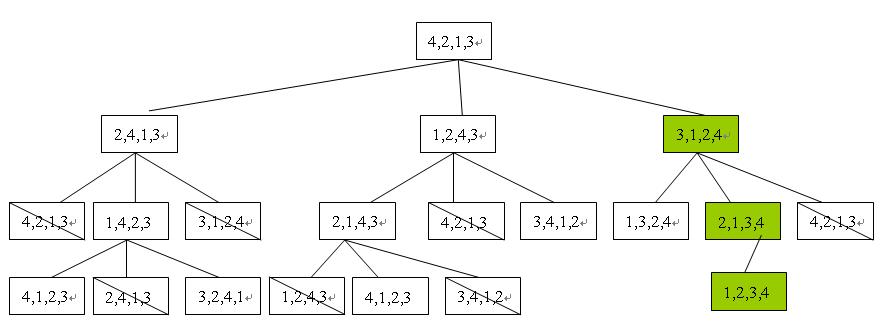
书中给出的解法就是采用深度优先的方式来遍历这棵搜索树，例如要排序[4,2,1,3]，最大反转次数不应该超过(4-1)*2=6次，所以搜索树的深度也不应大于6，搜索树如下图所示：

这里只列到第三层，其中被画斜线的方块由于和上层的某一节点的状态重复而无需再扩展下去（即便扩展也不可能比有相同状态的上层节点的代价少）。我们可以看到在右子树中的一个分支，只需要用3次反转即可完成，我们的目标是如何更为快速有效的找到这一分支。直观上我们可以看到：基本的搜索方法要先从左子树开始，所以要找到本例最佳的方案的代价是很高的（利用书中的算法需要查找292次）。

既然要遍历搜索树，就有广度优先和深度优先之分，可以分别用栈和队列来实现（当然也可以用递归的方法）。那么如何能更有效地解决问题呢？我们主要考虑一下几种方法：

（1）       爬山法

该方法是在深度优先的搜索过程中使用贪心方法确定搜索方向，它实际上是一种深度优先搜索策略。爬山法采用启发式侧读来排序节点的扩展顺序，其关键点就在于测度函数f(n)的定义。我们来看一下如何为上例定制代价函数f(n)，以快速找到右子树中最好的那个分支（很像贪心算法，呵呵）。

我们看到在[1,2,4,3]中，[1,2,3]已经相对有序，而[4]位与他们之间，要想另整体有序，需要4次反转；而[3,1,2,4]中，由于[4]已经就位，剩下的数变成了长度为3的子队列，而子队列中[1,2]有序，令其全体有序只需要2次反转。

所以我们的代价函数应该如下定义：

1 从当前状态的最后一个饼开始搜索，如果该饼在其应该在的位置（中间断开不算），则跳过；

2 自后向前的搜索过程中，如果碰到两个数不相邻的情况，就+1

这样我们就可以在本例中迅速找到最优分枝。因为在树的第一层

f(2,4,1,3)=3，f(1,2,4,3)=2，f(3,1,2,4)=1，所以我们选择[3,1,2,4]那一枝，而在[3,1,2,4]的下一层：

f(1,3,2,4)=2，f(2,1,3,4)=1，f(4,2,1,3)=2，所以我们又找到了最佳的路径。

上面方法看似不错，但是数字比较多的时候呢？我们来看书中给出的10个数的例子：

[3,2,1,6,5,4,9,8,7,0]，程序给出的最佳翻转序列为{ 4,8,6,8,4,9}（从0开始算起）

那么，对于搜索树的第一层，按照上面的算法我计算的结果如下：

f(2,3,1,6,5,4,9,8,7,0)=4

       f(1,2,3,6,5,4,9,8,7,0)=3

       f(6,1,2,3,5,4,9,8,7,0)=4

       f(5,6,1,2,3,4,9,8,7,0)=3

       f(4,5,6,1,2,3,9,8,7,0)=3

       f(9,4,5,6,1,2,3,8,7,0)=4

       f(8,9,4,5,6,1,2,3,7,0)=4

f(7,8,9,4,5,6,1,2,3,0)=3

f(0,7,8,9,4,5,6,1,2,3)=3

我们看到有4个分支的结果和最佳结果相同，也就是说，我们目前的代价函数还不够“一击致命”，但是这已经比书中的结果要好一些，起码我们能更快地找到最佳方案，这使得我们在此后的剪枝过程更加高效。

爬山法的伪代码如下：

1 构造由根组成的单元素栈S

2 IF Top(s)是目标节点 THEN 停止；

3 Pop(s);

4 S的子节点按照启发式测度，由小到大的顺序压入S

5 IF 栈空 Then 失败

Else 返回2

 

              如果有时间我会把爬山法解决的烙饼问题贴在后面。

（2）       Best-First搜索策略

最佳优先搜索策略结合了深度优先和广度优先二者的优点，它采取的策略是根据评价函数，在目前产生的所有节点中选择具有最小代价值的节点进行扩展。该策略具有全局优化的观念，而爬山法则只具有局部优化的能力。具体用小根堆来实现搜索树就可以了，这里不再赘述。

（3）       A*算法

如果我们把下棋比喻成解决问题，则爬山法和Best-First算法就是两个只能“看”未来一步棋的玩家。而A*算法则至少能够“看”到未来的两步棋。

我们知道，搜索树的每一个节点的代价f*(n)=g(n)+h*(n)。其中，g(n)为从根节点到节点n的代价，这个值我们是可求的；h*(n)则是从n节点到目标节点的代价，这个值我们是无法实际算出的，只能进行估计。我们可以用下一层节点代价的最小者来替代h*(n)，这也就是“看”了两步棋。可以证明，如果A*算法找到了一个解，那它一定是优化解。A*算法的描述如下：

1．  使用BestFirst搜索树

2．  按照上面所述对下层点n进行计算获得f*(n)的估计值f(n)，并取其最小者进行扩展。

3．  若找到目标节点，则算法停止，返回优化解

总结：归根到底，烙饼问题之所以难于在多项式时间内解决的关键就在于我们无法为搜索树中的每一条边设定一个合理的权值。在这里，每条边的权值都是1，因为从上一个状态节点到下一个状态节点之需要一次翻转。所以我们不能简单地把每个节点的代价定义为翻转次数，而应该根据其距离最终解的接近程度来给出一个数值，而这恰恰就是该问题的难点。但是无论上面哪一种方法，都需要我们确定搜索树各个边的代价是多少，然后才能进行要么广度优先、要么深度优先、要么A*算法的估计代价。所以，在给出一个合理的代价之前，我们所有的努力都只能是帮忙“加速”，而无法真正在多项式时间内解决问题。

 

#include<iostream>
#include<fstream>
#include<vector>
#include<algorithm>
#include<ctime>
using namespace std;

class Pancake{
 public:
  Pancake() {}
  void print() const;
  void process();               //显示最优解的翻转过程
  int run(const int cake_arr[], int size, bool show=true);
  void calc_range(int na, int nb);

 private: 
  Pancake(const Pancake&);
  Pancake& operator=(const Pancake&);
  inline bool init(const int cake_arr[], int& size);
  void search_cake(int size, int step, int least_swap_old);
  void reverse_cake(int index) { //翻转0到index间的烙饼
    ++count_reverse; 
    std::reverse(&cake[0], &cake[index + 1]);
  }
  
  bool next_search_cake(int pos, int size, int step, int least_swap)
  {
    if (least_swap + step >= get_min_swap()) return true;
    cake_swap[step] = pos;
    reverse_cake(pos);
    search_cake(size,step,least_swap);
    reverse_cake(pos);
    return false;
  }
  
  int get_min_swap() const { return result.size();}
  
  void output(int i, const std::string& sep, int width) const {
    cout.width(width);
    cout << i << sep;
  }
  
  void output(const std::string& sep, int width) const {
    cout.width(width);
    cout << sep;
  }
  
  vector<int> cake_old;        //要处理的原烙饼数组
  vector<int> cake;            //当前各个烙饼的状态
  vector<int> result;          //最优解中，每次翻转的烙饼位置
  vector<int> cake_swap;       //每次翻转的烙饼位置
  vector<int> cake_order;      //第step+1次翻转时，翻转位置的优先顺序
  int min_swap_init;           //最优解的翻转次数初始值
  int count_search;            //search_cake被调用次数
  int count_reverse;           //reverse_cake被调用次数
};


void Pancake::print() const
{
  int min_swap = get_min_swap();
  if (min_swap == 0) return; 
  cout << "minimal_swap initial: " << min_swap_init 
       << "  final: "<< min_swap 
       << "\nsearch/reverse function was called: " << count_search
       << "/" << count_reverse << " times\nsolution: ";
  for (int i = 0; i < min_swap; ++i) cout << result[i] << " ";
  cout<< "\n\n";
}

void Pancake::process()
{
  int min_swap = get_min_swap(); 
  if (min_swap == 0) return;
  cake.assign(cake_old.begin(), cake_old.end());
  int cake_size = cake_old.size();
  const int width = 3, width2 = 2 * width + 3;
  output("No.", width2);
  for (int j = 0; j < cake_size; ++j) output(j," ",width);   
  cout << "\n";     
  output("old:", width2);    
  
  for (int j = 0; j < cake_size; ++j) output(cake[j]," ",width);  
  cout << "\n";        
  
  for (int i = 0; i < min_swap; ++i){
    reverse_cake(result[i]);
    output(i + 1," ",width);  
    output(result[i],": ",width);  
    for (int j = 0; j < cake_size; ++j)  output(cake[j]," ",width);  
    cout << "\n";
  }
  cout << "\n\n";
}

bool Pancake::init(const int cake_arr[], int& size)
{
  result.clear();
  if (cake_arr == NULL) return false;
  cake_swap.resize(size * 2);
  cake_order.resize(size * size * 2);
  count_search = 0;
  count_reverse = 0;
  cake_old.assign(cake_arr,cake_arr + size);
  //去除末尾已就位的烙饼，修正烙饼数组大小。
  while (size > 1 && size - 1 == cake_arr[size - 1]) --size; 
  if (size <= 1) return false;
  
  cake.assign(cake_arr,cake_arr + size);
  for (int j = size - 1; ;) {           //计算一个解作为min_swap初始值。
    while(j > 0 && j == cake[j]) --j;
    if (j <= 0) break;
    int i = j;
    while (i >= 0 && cake[i] != j) --i;
    if (i != 0) {
      reverse_cake(i);
      result.push_back(i);
    }
    reverse_cake(j);
    result.push_back(j);
    --j;
  }
  cake.assign(cake_arr,cake_arr + size); //恢复原来的数组
  cake.push_back(size);                 //多放一个烙饼，避免后面的边界判断
  cake_swap[0] = 0;                     //假设第0步翻转的烙饼编号为0
  min_swap_init= get_min_swap();
  return true;
}

int Pancake::run(const int cake_arr[], int size, bool show)
{
  if (! init(cake_arr, size)) return 0;
  int least_swap = 0;
  //size = cake.size() - 1;
  for (int i = 0; i < size; ++i)
    if (cake[i] - cake[i + 1] + 1u > 2) ++least_swap;  
  if (get_min_swap() != least_swap) search_cake(size, 0, least_swap);
  if (show) print();
  return get_min_swap();
}

void Pancake::search_cake(int size, int step, int least_swap_old)
{
  ++count_search;
  while (size > 1 && size - 1 == (int)cake[size - 1]) --size; //去除末尾已就位的烙饼
  int *first = &cake_order[step * cake.size()];
  int *last = first + size;
  int *low = first, *high = first + size;

  for (int pos = size - 1, last_swap = cake_swap[step++]; pos > 0; --pos){
    if (pos == last_swap) continue;
    int least_swap = least_swap_old ;
    if (cake[pos] - cake[pos + 1] + 1u <= 2) ++least_swap;
    if (cake[0] - cake[pos + 1] + 1u <= 2) --least_swap;

    if (least_swap + step >= get_min_swap()) continue;
    if (least_swap == 0) {
      cake_swap[step] = pos;
      result.assign(&cake_swap[1], &cake_swap[step + 1]);
      return;
    }
    
    //根据least_swap值大小，分别保存pos值，并先处理使least_swap_old减小1的翻转
    if (least_swap == least_swap_old) *low++ =pos;
    else if (least_swap > least_swap_old) *--high =pos;
    else next_search_cake(pos, size, step, least_swap);   
  }

  //再处理使least_swap_old不变的翻转
  for(int *p = first; p < low; p++)
    if (next_search_cake(*p, size, step, least_swap_old)) return;
    
  //最后处理使least_swap_old增加1的翻转
  for(int *p = high; p < last; p++)
    if (next_search_cake(*p, size, step, least_swap_old + 1)) return;
}

void Pancake::calc_range(int na, int nb)
{
  if (na > nb || na <= 0) return;
  clock_t ta = clock();
  static std::vector<int> arr;
  arr.resize(nb);
  unsigned long long total_search = 0;
  unsigned long long total_reverse = 0;
  for (int j = na; j <= nb; ++j) {
    for (int i = 0; i < j; ++i) arr[i] = i;
    int max = 0;
    unsigned long long count_s = 0;
    unsigned long long count_r = 0;
    clock_t tb = clock();
    while (std::next_permutation(&arr[0], &arr[j])) {    
      int tmp = run(&arr[0],j,0);
      if (tmp > max) max = tmp;
      count_s += count_search;
      count_r += count_reverse;
    }
    total_search +=  count_s;
    total_reverse += count_r;
    output(j, " ",2);
    output(max,"     time: ",3);
    output(clock() - tb,"  ms  ",8);
    cout << " search/reverse: " << count_s << "/" << count_r << "\n";
  }
  cout << "  total  search/reverse: " << total_search
       << "/" << total_reverse << "\n"
       << "time :  " << clock() - ta << "  ms\n";
}

int main()
{
  int aa[10]={ 3,2,1,6,5,4,9,8,7,0};
  //int ab[10]={ 4,8,3,1,5,2,9,6,7,0};
 // int ac[]={1,0, 4, 3, 2};
  Pancake cake;
  cake.run(aa,10);
  cake.process();
  //cake.run(ab,10);
  //cake.process(); 
  //cake.run(ac,sizeof(ac)/sizeof(ac[0]));
  //cake.process();  
  cake.calc_range(1,9);
}

减少遍历次数：

 

1 减小“最少翻转次数上限值”的初始值，采用前面提到的翻转方案，取其翻转次数为初始值。对书中的例子{3,2,1,6,5,4,9,8,7,0}，初始值可以取10。

 

2 避免出现已处理过的状态一定会减少遍历吗？答案是否定的，深度优先遍历，必须遍历完一个子树，才能遍历下一个子树，如果一个解在某层比较靠后位置，若不允许处理已出现过的状态时，可能要经过很多次搜索，才能找到这个解，但允许处理已出现过的状态时，可能会很快找到这个解，并减小“最少翻转次数的上限值”，使更多的分支能被剪掉，反而能减少遍历的节点数。比如说，两个子树A、B，搜索子树A，100次后可得到一个对应翻转次数为20的解，搜索子树B，20次后可得到翻转次数为10的解，不允许处理已出现过的状态，就会花100次遍历完子树A后，才开始遍历B，但允许翻转回上一次状态，搜索会在A、B间交叉进行，就可能只要70次找到子树B的那个解（翻转次数为10+2=12），此时，翻转次数上限值比较小，可忽略更多不必要的搜索。以书中的{3,2,1,6,5,4,9,8,7,0}为例，按程序（1.3_pancake_1.cpp），不允许翻转回上次状态时需搜索195次，而允许翻转回上次状态时只要搜索116次。

 

3 如果最后的几个烙饼已经就位，只须考虑前面的几个烙饼。对状态(0,1,3,4,2,5,6)，编号为5和6的烙饼已经就位，只须考虑前5个烙饼，即状态(0,1,3,4,2)。如果一个最优解，从某次翻转开始移动了一个已经就位的烙饼，且该烙饼后的所有烙饼都已经就位，那么对这个解法，从这次翻转开始得到的一系列状态，从中移除这个烙饼，可得到一系列新的状态。必然可以设计出一个新的解法对应这系列新的状态，而该解法所用的翻转次数不会比原来的多。

 

4 估计每个状态还需要翻转的最少次数（即下限值），加上当前的深度，如果大等于上限值，就无需继续遍历。这个下限值可以这样确定：从最后一个位置开始，往前找到第一个与最终结果位置不同的烙饼编号（也就是说排除最后几个已经就位的烙饼），从该位置到第一个位置，计算相邻的烙饼的编号不连续的次数，再加上1。每次翻转最多只能使不连续的次数减少1，但很多人会忽略掉这个情况：最大的烙饼没有就位时，必然需要一次翻转使其就位，而这次翻转却不改变不连续次数。（可以在最后面增加一个更大的烙饼，使这次翻转可以改变不连续数。）如：对状态(0,1,3,4,2,5,6)等同于状态(0,1,3,4,2)，由于1、3和4、2不连续，因而下限值为2+1=3。下限值也可以这样确定：在最后面增加一个比所有烙饼都大的已经就位的烙饼，然后再计算不连续数。如：(0,1,3,4,2)，可以看作(0,1,3,4,2,5)，1和3 、4和2 、2和5这三个不连续，下限值为3。

 

5多数情况下，翻转次数的上限值越大，搜索次数就越多。可以采用贪心算法，通过调整每次所有可能翻转的优先顺序，尽快找到一个解，从而减少搜索次数。比如，优先搜索使“下限值”减少的翻转，其次是使“下限值”不变的翻转，最后才搜索使“下限值”增加的翻转。对“下限值”不变的翻转，还可以根据其下次的翻转对“下限值”的影响，再重新排序。由于进行了优先排序，翻转回上一次状态能减少搜索次数的可能性得到进一步降低。

 

6 其它剪枝方法：

假设进行第m次翻转时，“上限值”为min_swap。

如果翻转某个位置的烙饼能使所有烙饼就位（即翻转次数刚好为m），则翻转其它位置的烙饼，能得到的最少翻转次数必然大等m，因而这些位置都可以不搜索。

如果在某个位置的翻转后，“下限值”为k，并且 k+m>=min_swap，则对所有的使新“下限值”kk大等于k的翻转，都有 kk+m>=min_swap，因而都可以不搜索。该剪枝方法是对上面的“调整翻转优先顺序”的进一步补充。

 

另外，翻转某个烙饼时，只有两个烙饼位置的改变才对“下限值”有影响，因而可以记录每个状态的“下限值”，进行下一次翻转时，只须通过几次比较，就可以确定新状态的“下限值”。（判断不连续次数时，最好写成 -1<=x && x<=1， 而不是x==1 || x==-1。对于 int x; a<=x && x<=b，编译器可以将其优化为 unsigned (x-a) <= b-a。）

 

 

结果：

 

对书上的例子{3,2,1,6,5,4,9,8,7,0}：

	翻转回上次状态	搜索函数被调用次数	翻转函数被调用次数
1.3_pancake_2	不允许	29	66
1.3_pancake_2	允许	33	74
1.3_pancake_1	不允许	195	398
1.3_pancake_1	允许	116	240

（这个例子比较特殊，代码1.3_pancake_2.cpp（与1.3_pancake_1.cpp的最主要区别在于，增加了对翻转优先顺序的判断， 代码下载），在不允许翻转回上次状态且取min_swap的初始值为2*10-2=18时，调用搜索函数29次，翻转函数56次）。

 

搜索顺序对结果影响很大，如果将1.3_pancake_2.cpp第152行：

for (int pos=1, last_swap=cake_swap[step++]; pos<size; ++pos){

这一行改为：

for (int pos=size-1, last_swap=cake_swap[step++]; pos>=1; --pos){

仅仅调整了搜索顺序，调用搜索函数次数由29次降到11次（对应的翻转方法：9，6，9，6，9，6），求第1个烙饼数到第10个烙饼数，所用的总时间也由原来的38秒降到21秒。）

 

补充：

 

在网上下了《编程之美》“第6刷”的源代码，结果在编译时存在以下问题：

1 Assert 应该是 assert

2 m_arrSwap 未被定义，应该改为m_SwapArray

3 Init函数两个for循环，后一个没定义变量i，应该将i 改为 int i

另外，每运行一次Run函数，就会调用Init函数，就会申请新的内存，但却没有释放原来的内存，会造成内存泄漏。if(step + nEstimate > m_nMaxSwap) 这句还会造成后面对m_ReverseCakeArraySwap数组的越界访问，使程序不能正常运行。

 

书上程序的低效主要是由于进行剪枝判断时，没有考虑好边界条件，可进行如下修改：

1  if(step + nEstimate > m_nMaxSwap)  > 改为 >=。

2  判断下界时，如果最大的烙饼不在最后一个位置，则要多翻转一次，因而在LowerBound函数return ret; 前插入一行：

if (pCakeArray[nCakeCnt-1] != nCakeCnt-1) ret++; 。

3  n个烙饼，翻转最大的n-2烙饼最多需要2*(n-2)次，剩下的2个最多1次，因而上限值为2*n-3，因此，m_nMaxSwap初始值可以取2*n-3+1=2*n-2，这样每步与m_nMaxSwap的判断就可以取大等于号。

4  采用书上提到的确定“上限值”的方法，直接构建一个初始解，取其翻转次数为m_nMaxSwap的初始值。

 

1和2任改一处，都能使搜索次数从172126降到两万多，两处都改，搜索次数降到3475。若再改动第3处，搜索次数降到2989；若采用4的方法（此时初始值为10），搜索次数可降到1045。