前言
- 在上篇文章:以最简单的斐波拉契数列为例子初步认识动态规划中末尾,有讲到动态规划的解题思路,但在解析斐波拉契数列时,也许是大家对它很熟悉,所以对于递归 + 记忆化这一步骤感受可能不是特别深。接下来,将严格按照上篇文章所说的解题思路来解决计算路径总数问题。
一、计算路径总数问题描述

根据图中问题的描述,其中一个解法其实可以用高中所学的排列组合来做,奈何本人高中数学是体育老师教的,这里就不献丑了! 咱们作为一名程序员,还是通过程序来解决吧~由文章主题可知,计算路径总数是一道动态规划的题,根据咱们在上篇文章的总结,要解决动态规划的题目要按照如下几个步骤来触发(针对刚接触动态规划的初学者而言):
1.分析它的递归关系
2.递归的重复计算,考虑使用缓存
3.状态的定义
4.推导出动态转移方程
5.最优子结构(最值问题)
ps: 上述的第1、2步就是上篇文章所说的递归 + 记忆化。
同时最优子结构(最值问题)在本题中并没有要求求解,但因为有记忆化功能,我们只需从缓存中去比较最值问题即可。接下来,咱们按照这个思路一步步分析
ps:下文中所说的[m, n]位置指的就是题目中星星所处的位置
二、分析它的递归关系
- 由题目可知,要计算从起点[0, 0]的位置到[m, n]位置的所有走法,可以把它拆解成许多个小问题,比如:拆解成从[0, 1]到[m, n]有多少种走法与从[1, 0]到[m, n]有多少种走法,然后把它们两个子问题的结果相加就是从[0, 0]到[m, n]的走法了。具体可以参考下图:
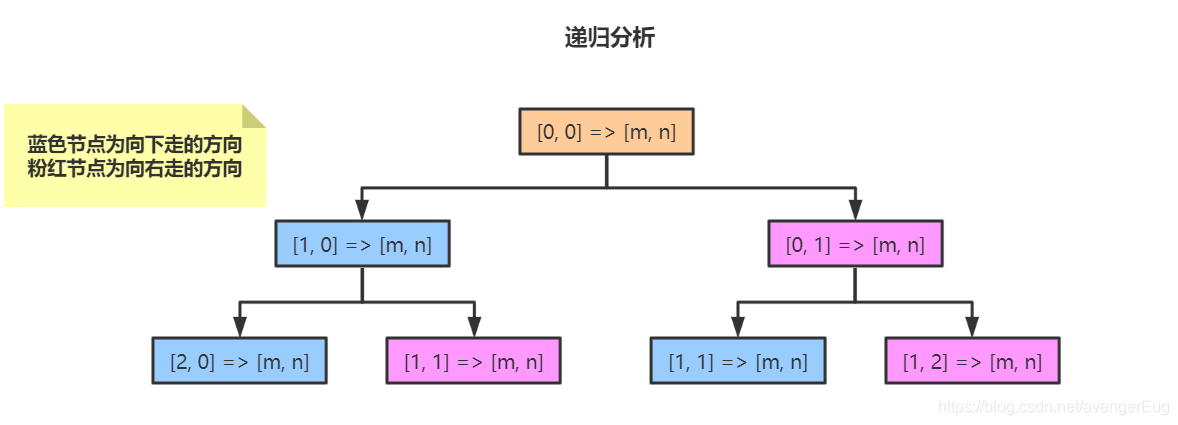
由上图可知(只画了部分的子问题),求[0, 0]到[m, n]的所有走法问题拆解成了若干个子问题,我们只需要把每个子问题求解出来,最后再将这些子问题累加即可。
三、递归的重复计算,考虑使用缓存
- 由上图可知,在计算[1, 0] => [m, n]时,拆解出来的子问题计算了一次[1, 1] => [m, n]的所有走法。而在计算[0, 1] => [m, n]时,拆解出来的子问题又计算了一次[1, 1] => [m, n]。 这个斐波拉契数列类似,都做了重复的操作,为了优化它,我们可以添加缓存。在斐波拉契数列中,我们最开始是使用hashMap做为缓存,但后续认为额外占用了内存,不是最优解,于是我们使用了一个数组作为缓存。在此处,我们也可以开启一个和矩阵一模一样的二维数组dp[][],但内部每个元素存储的值是当前位置到[m, n]节点的走法之和。
四、状态的定义
- 在上述第三章节中,有说到使用缓存,而且这个缓存就是一个二维数组dp[][],所以我们定义dp中的每个元素存储的内容就是当前位置到[m, n]的所有走法。
五、推导出动态转移方程
- 此步骤是动态规划的核心,有了它,题目差不多完成一半了!在步骤中,咱们死扣条件,从题目描述中找出隐藏的一些内容:

题目中描述,小人在当前格子中只能向下或者向右走。咱们从这句话中可以得到哪些信息呢?假如小人走到了[0, n]的位置上,即如图所示:
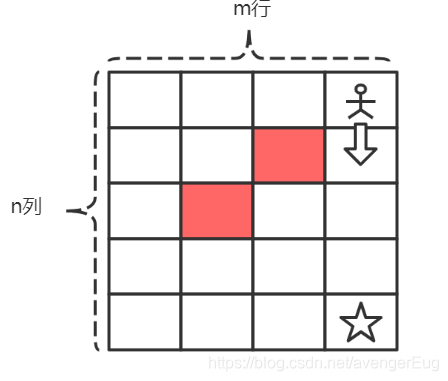
那么是不是代表着,[0, n]这个位置的走法只有一种(只能往下走),或者假如说小人走到了[m, 0]的位置上,如图所示:
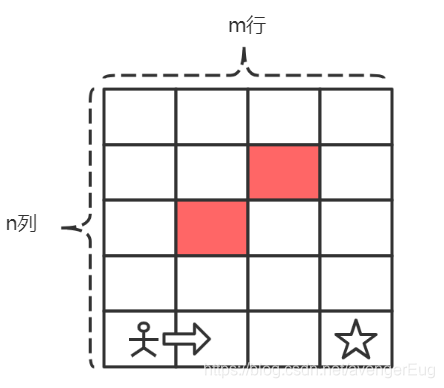
那是不是也代表着[0, n]这个位置上的走法也只有一种(只能往右走)。于是,我们可以知道终点([m, n]的位置)所处的行和列的走法都只有一种。因此,整个矩阵变成了如下的样子:
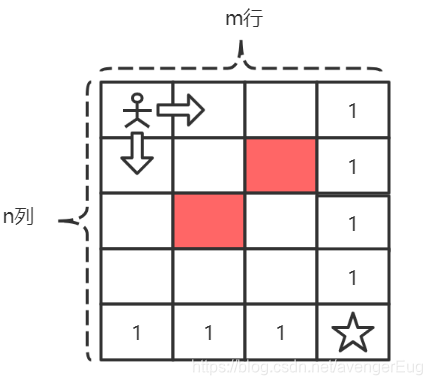
又因为,每个位置只能向下和向右走,那大家猜想下,下图中标绿的位置的走法有几种呢?
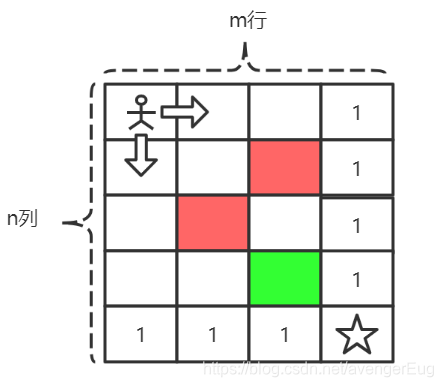
答案是两种,那么咱们是不是了解了一些规律了呢?矩阵中的任意位置走向[m, n]的走法等于当前位置下方相邻节点的走法加上右方相邻节点的走法。所以,动态转移方程就是:dp[x][y] = dp[x + 1, y] + dp[x, y + 1],为了方便,我把每个格子所有的走法都填充至矩阵中,如下所示:
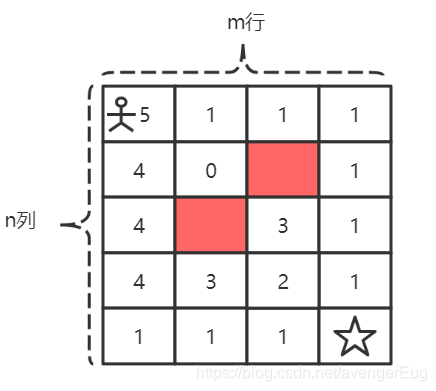
ps: 因为红色格子是石头,所以不能走,因此在[1, 1]这个位置上是死路,无法走向[m, n],所以它的值为0。
综上所述,以动态规划来解决此问题的代码如下(仅供参考):public static int pathDynamic(boolean p[][]) { // 状态的定义,一个二维数组,存放的是每个节点到[m, n] // 节点的走法。也是一个缓存 int dp[][] = new int[p.length][p[0].length]; // 从后往前推,因为我们通过题目条件唯一知道的就是 // 最右侧和最下侧的节点的走法只有一种, // 进而开始递推前面的节点 for (int i = p.length - 2; i >= 0; i--) { // 初始化当前行的最右边的列为1 dp[i][p[i].length - 1] = 1; for (int j = p[i].length - 2; j >= 0; j--) { // 初始化当前列的最下面的行为1 dp[p.length - 1][j] = 1; // p[i][j]为false,则表示它是石头 // 前面图中所示的绿色节点对应的值,并把它缓存起来 dp[i][j] = !p[i][j] ? 0 : dp[i][j + 1] + dp[i + 1][j]; } } return dp[0][0]; } public static void main(String[] args) { // 5行,4列 ==> // 行:[0, 4] [0, p.lenth - 1] // 列:[0, 3] [0, p[0].length - 1] boolean p[][] = new boolean[][] { {true, true, true, true}, {true, true, false, true}, {true, false, true, true}, {true, true, true, true}, {true, true, true, true}, }; System.out.println(pathDynamic(p)); }
六、最优子结构
- 由上分析可知,在dp二维数组中存储了所有节点到[m, n]节点的走法的和。假设现在要求哪个节点一定不能走向[m, n]? 我们从眼睛可以很容易的看出,一定是[1, 1]这个节点,但对计算机而言,它并不能一看就知道,它需要计算,在这种问题下,我们可以直接从dp二维数组中找出哪些节点存储的值为0即可!
七、总结
- 本次,咱们从递归 => 记忆化 => 状态定义 => 状态转移方程 => 最优子结构的流程解决了这么一个计算路径总数的题目。文中也说了,最难的部分就是动态转移方程的推导了,我们必须要紧扣题目,找出所有隐藏的条件,再从这个条件出发(有可能是顺推也有可能是逆推),最终找出这么一个规律。
- 我们将动态转移方程定义出来后,一定要相信它,而不要再去回溯,验证是不是对的。比如在我要去验证下[2, 2]这个节点到[m, n]的走法到底是不是3,走法少还没事,如果走法特别多的话,容易把自己绕晕!
- I am a slow walker, but I never walk backwards.





















 1825
1825











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








