Deriving the Poisson Distribution from the Binomial Distribution

At first glance, the  binomial distribution  and the  Poisson distribution  seem unrelated. But a closer look reveals a pretty interesting relationship. It turns out the Poisson distribution is just a special case of the binomial -- where the number of trials is large, and the probability of success in any given one is small. 

In this post I'll walk through a simple proof showing that the Poisson distribution is really just the binomial with n approaching infinity and p approaching zero. 

The Proof
The binomial distribution works when we have a fixed number of events n, each with a constant probability of success p. Imagine we don't know the number of trials that will happen. Instead, we only know the average number of successes per time period. So we know the rate of successes per day, but not the number of trials n or the probability of success p that led to that rate. 

Define a number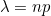  . Let this be the rate of successes per day. It's equal to np. That's the number of trials n -- however many there are -- times the chance of success p for each of those trials. Think of it like this: if the chance of success is p and we run n trials per day, we'll observe np successes per day on average. That's our observed success rate lambda. 

Recall that the binomial distribution looks like this: 



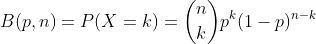
As mentioned above, let's define lambda as follows:



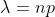
Solving for p, we get:



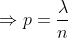
What we're going to do here is substitute this expression for p into the binomial distribution above, and take the limit as n goes to infinity, and try to come up with something useful. That is,



Pulling out the constants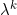   and 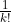  and splitting the term on the right that's to the power of (n-k) into a term to the power of n and one to the power of -k, we get



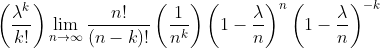
Now let's take the limit of this right-hand side one term at a time. We'll do this in three steps. The first step is to find the limit of 



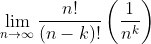
In the numerator, we can expand n! into n terms of (n)(n-1)(n-2)...(1). And in the denominator, we can expand (n-k) into n-k terms of (n-k)(n-k-1)(n-k-2)...(1). That is,



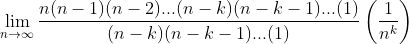
Written this way, it's clear that many of terms on the top and bottom cancel out. The (n-k)(n-k-1)...(1) terms cancel from both the numerator and denominator, leaving the following:



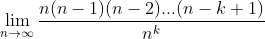
Since we canceled out n-k terms, the numerator here is left with k terms, from n to n-k+1. So this has k terms in the numerator, and k terms in the denominator since n is to the power of k. Expanding out the numerator and denominator we can rewrite this as:



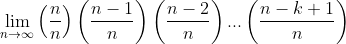
This has k terms. Clearly, every one of these k terms approaches 1 as n approaches infinity. So we know this portion of the problem just simplifies to one. So we're done with the first step. 

The second step is to find the limit of the term in the middle of our equation, which is 



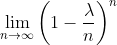
Recall that the definition of e = 2.718... is given by the following:



Our goal here is to find a way to manipulate our expression to look more like the definition of e, which we know the limit of. Let's define a number x as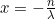  . Now let's substitute this into our expression and take the limit as follows:



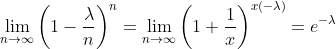
This terms just simplifies to e^(-lambda). So we're done with our second step. That leaves only one more term for us to find the limit of. Our third and final step is to find the limit of the last term on the right, which is



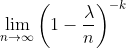
This is pretty simple. As n approaches infinity, this term becomes 1^(-k) which is equal to one. And that takes care of our last term. 

Putting these three results together, we can rewrite our original limit as



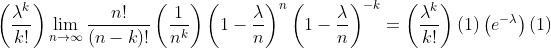
This just simplifies to the following:



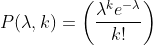
This is equal to the familiar probability density function for the  Poisson distribution , which gives us the probability of k successes per period given our parameter lambda. So we've shown that the Poisson distribution is just a special case of the binomial, in which the number of n trials grows to infinity and the chance of success in any particular trial approaches zero. And that completes the proof.