模拟竖式计算方式处理数据的加减操作-Java描述

算法题目经常会遇到给你两个二进制表示的正整数，求两个二进制数的和，结果仍以二进制表示，二进制数字符串长度小于等于长度，仅仅使用Java语言自带的大整数方法转换也是不行的已经超出了计算机的表示范围，无法直接将二进制字符串转换成十进制数相加再将结果转化成对应的二进制字符串，针对这种情况我们只能模拟数学上的竖式计算方法解决这个求和问题。

具体操作如下：

回想下我们在做竖式计算时，优先将两个数字从右向左，按照数位的最低位依次对齐，长度不够的高位补0，直到两个数的长度一致，每个数位一、一对齐形如：

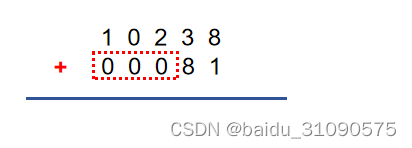
从最右侧的地位依次计算每一个数位上两个数字之和，在计算过程中我们需要一个临时变量carry记录上一个数位上进位的数字大小，初始在最低位，carry默认值为0; 因此对于一般情况，我们计算第 i 个数位上的和由三部分内容组成，上一个数位进位的carry值和当前数位上的两个数之和，然后将得到和与对应的进制基数（当前二进制基数为2）相除，将取整的值赋给carry，作为进位，将取的余数作为当前数位的计算结果，重复上述动作处理下一个数位 i+1的结果，直到处理完所有数位，注意在最后需要判断carry大于0还是小于0，大于0表示进位，小于0表示借位。

竖式计算二进制加法：

String binary1 = "1000011101010";
String binary2 = "111111";

binary1 + binary2 = result

result = “1000100101001”

    public static String binaryAdd(String binary1, String binary2) {
        StringBuffer sb = new StringBuffer();
        int maxLen = Math.max(binary1.length(), binary2.length());
        int carry = 0;
        for (int i = 0; i < maxLen; i++) {
            carry += i < binary1.length() ? (binary1.charAt(binary1.length() - 1 - i) - '0') : 0;
            carry += i < binary2.length() ? (binary2.charAt(binary2.length() - 1 - i) - '0') : 0;
            sb.insert(0, (char) (carry % 2 + '0'));
            carry /= 2;
        }
        if (carry > 0) {
            sb.insert(0, '1');
        }
        return sb.toString();
    }

String binary1 = "1000011101010";
String binary2 = "111111";

result= “1000010101011”

binary1 - binary2 = result

    public static String binarySubtract(String binary1, String binary2) {
        StringBuffer sb = new StringBuffer();
        int maxLen = Math.max(binary1.length(), binary2.length());
        int carry = 0;
        for (int i = 0; i < maxLen; i++) {
            carry += i < binary1.length() ? (binary1.charAt(binary1.length() - 1 - i) - '0') : 0;
            carry -= i < binary2.length() ? (binary2.charAt(binary2.length() - 1 - i) - '0') : 0;  //减法与加法差异点1
            if (carry >= 0) {
                sb.insert(0, (char) (carry % 2 + '0'));
                carry /= 2;
            } else {
                sb.insert(0, (char) (2 + carry + '0'));     //减法与加法差异点2
                carry = -1;                                       //减法与加法差异点3
            }
        }
        if (carry < 0) {
            sb.insert(0, '0');                          //减法与加法差异点4
        }
        return sb.toString();
    }