Declare:



is a square-free number.
is the Euler's totient function. find:






There are infinite number of
 原博客详情请见(转载自)http://blog.csdn.net/wust_zzwh/article/details/51966450
原博客详情请见(转载自)http://blog.csdn.net/wust_zzwh/article/details/51966450Input
Multiple test cases(test cases), one line per case. Each line contains three integers,
and
.


Output
For each case, output a single line with one integer, ans.Sample Input
Sample Output
这个题考的是欧拉函数和指数循环节,我只是以这种方式想做个笔记才搞的这个博客
这个题考的欧拉函数的积性函数性质:
①当gcd(a,b)==1即a与b互质时,有phi(a*b)=phi(a)*phi(b);
②phi(m*n*p)=p*phi(m*n),其中p与n/p互质,至于原因,把这个式子按照欧拉函数的基础通式展开再推一推就得到了;
然后就可以有:
分成两部分求:
.....p是素数,素数的欧拉值就是p-1;
到这里前两和式是可以合并的,考虑和式的上下限,含义不同,第二项的i表示的p的倍数i*p才是第一项i的含义,相当于第二项刚好把第一项补齐了,那么从1到m没有遗漏,而且第二项的i用第一项替换后里面也是n/p;最终
n/p和m/p看成整体,那么设原先求的为f(n,m),所以f(n,m)=(p的欧拉值)*f(n/p,m)+f(n,m/p);
第二部分k的超级幂:用欧拉的定理:指数循环节
每次往幂次上一层模就取一次欧拉值,只有1的欧拉值等一自己,其他数的欧拉值都是小于自己的,所以模会不断变小至1,显然对1取模结果就是0,所以无限就变得有限了
代码:
#include <stdio.h> #include <algorithm> #include <iostream> #include <string.h> #include <set> #include <map> #include <vector> #include <queue> #include <string> #include <math.h> using namespace std; typedef long long LL; const LL MOD=1000000000+7; const LL maxn=10000000+7; LL el[maxn],sumel[maxn]; LL N,M,P; bool isprime[maxn]; LL prime[maxn/5]; LL total; LL fac[maxn/3]; void sox(LL m)//线性时间筛出欧拉值和质数 { //elu(); memset(el,0,sizeof(el)); memset(sumel,0,sizeof(sumel)); el[1]=1;sumel[1]=1; memset(isprime,false,sizeof(isprime)); memset(prime,0,sizeof(prime)); total=0; isprime[0]=isprime[1]=false; for(LL i=2;i<=m;i++) { if(!isprime[i]) { prime[total++]=i; el[i]=i-1; } for(LL j=0;j<total;j++) { if(i*prime[j]>m)break; isprime[i*prime[j]]=true; if(i%prime[j]==0) { el[i*prime[j]]=el[i]*prime[j]; break; } else { el[i*prime[j]]=el[i]*(prime[j]-1); } } sumel[i]=sumel[i-1]+el[i]; } memset(isprime,false,sizeof(isprime)); for(int i=0;i<total;i++) { isprime[prime[i]]=true; } } LL f(LL m,LL n,LL i)//计算本题中的k { //printf("fac=%lld n=%lld i=%lld\n",fac[i],n,i); if(m==0)return 0; if(n==1) { return sumel[m]%MOD; } return (fac[i]-1)*f(m,n/fac[i],i-1)%MOD+f(m/fac[i],n,i)%MOD; } LL cir(LL p,LL sum)//指数为1时的循环次数 { if(p==1)return sum; return cir(el[p],sum+1); } LL fast(LL x,LL n,LL mo) { LL ans=1; while(n>0) { if(n&1)ans=ans*x%mo; x=x*x%mo; n>>=1; } if(ans<=0)ans+=mo; return ans; } LL cal(LL sum,LL val,LL mo,LL k)//计算超级幂 { if(sum==1){/*printf("%lld %lld\n",el[mo],mo);*/return val%mo+mo;} LL ans=cal(sum-1,val,el[mo],k); return (fast(k,ans,mo))%mo+mo; } int main() { sox(maxn-1); //for(int i=1;i<=9;i++)printf("%lld\n",el[i]); while(scanf("%lld%lld%lld",&N,&M,&P)!=-1) { LL t=0,NN=N; for(LL i=0;i<total&&prime[i]*prime[i]<=NN;i++) { if(NN%prime[i]==0) { fac[t++]=prime[i]; if(isprime[NN/prime[i]]) { fac[t++]=NN/prime[i]; } NN/=prime[i]; } } if(t==0)fac[t++]=N; //printf("t=%lld\n",t); sort(fac,fac+t); /*for(int i=0;i<t;i++) { printf("%lld\n",fac[i]); }*/ LL a1=f(M,N,t-1)%MOD; //puts("a"); LL cs=cir(P,0); //puts("a"); LL ans=cal(cs,a1,P,a1)%P; printf("%lld\n",ans); } return 0; }
hdu 5728 PowMod
最新推荐文章于 2021-07-08 19:01:28 发布





























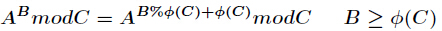















 786
786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








