TGD第七篇：一维应用——信号去噪和插值

从本篇开始，正式来到了实践应用部分，首先介绍的就是对于一维信号的应用（信号去噪和信号插值），感兴趣的朋友可直接阅读原始论文。理论部分可以详见前面的章节：

TGD 第一篇：初心——我想要为“阶梯函数”求导。

TGD 第二篇：破局——去除导数计算中的无穷小极限。

TGD 第三篇：革新——卷积计算导数的高效之路。

TGD 第四篇：初瞰——抗噪有效的定性计算。

TGD 第五篇：飞升——给多元函数的导数计算加上全景雷达。

TGD 第六篇：落地——离散序列的 TGD 计算。

一、基于 TGD 的信号去噪算法

1.1 去噪任务与信号连续性

在信号的产生、传输、处理、接收等过程中，不可避免地会引入噪声，如何去除噪声，减小噪声的影响，提取出有用的原始信号是始终是重要的信号处理研究方向。如何认为原始信号具有什么属性，如何认为噪声对原始信号带来的影响，是设计去噪算法的基础。

从传统认知上来讲，信号去噪建立在「 平滑假设 」之上，即“离散信号是由光滑函数上采样得到的一系列实数值，而噪声会以复杂的不规则性叠加在信号上，导致信号的不连续性”。

这里我就不多去分析传统的移动平均去噪、高斯平滑去噪、小波去噪、傅里叶阈值法去噪、全变分去噪等等已有去噪算法了，直接开始分析应该怎么基于 TGD 实现信号去噪。

其实很简单，就是源自高中生都会的一句话「 导数连续，则原函数光滑 」，即函数的变化率是连续的，那么函数本身就是光滑的。在 TGD 第六篇中我们用离散序列的 TGD 值来定义了该序列的变化率表征。为此，我可以大胆的说「 如果一个离散序列的 TGD 是连续的，则该离散序列是光滑的 」。

那么，基于 TGD 的信号去噪算法，总结而言一句话： 信号去噪就是（在保持信号固有特性的基础上）提升信号 TGD 的连续性 。

那么首先就需要 量化一个离散序列 TGD 的连续性 。注意到：离散序列的 TGD，其实也是一个离散序列，只不过每个数值表示原始序列的 TGD 值而已。

所以， 量化离散序列 TGD 的连续性，就是量化离散序列的连续性 ！

前人已经有人提出来了一种符合直觉的算法，即 Total Variation Denoising (全变分去噪、也称全变差去噪) 算法，并对序列的连续性进行了刻画。对于一个具有 $N$ 个元素的带噪离散序列 $X$ ，希望求得它的去噪后的序列 $Y^{\ast }$ ，可以通过以下最小化公式进行求解（为了方便描述，后文将其描述为最小化一个“损失函数（loss function）”）：

$\underset{Y\in {\mathbb{R}}^N}{\mathrm{minimize}}{\sum }_{i=1}^N(Y[i]-X[i]{)}^2+\lambda {\left({\sum }_{i=1}^{N-1}|Y[i+1]-Y[i]{|}^p\right)}^{\frac{1}{p}}$

其中 $\lambda$ 是一个正则化系数（也称为损失因子（loss factor）），当 $p=1$ 时，这个求解是一个强的凸优化问题，存在唯一解。当 $p=2$ 或者其他正整数值时，则是一个非凸优化问题。

全变分去噪算法的损失函数一共有两部分组成。第一部分为 ${\sum }_{i=1}^N(Y[i]-X[i]{)}^2$ ，指得到的去噪序列和原始带噪序列需要保有一定的相似性， $Y$ 是源自 $X$ 的，不能差别太大。损失函数的第二部分 ${\left({\sum }_{i=1}^{N-1}|Y[i+1]-Y[i]{|}^p\right)}^{\frac{1}{p}}$ 则是对序列 $Y$ 连续性的刻画，序列 $Y$ 中相邻两点之差的 ${\ell }_p$ 范数（ ${\ell }_p$ -norm）和越小，则序列 $Y$ 的连续性越高。整体来看，这个算法就是在保持序列 $Y$ 与带噪序列 $X$ 的相似性基础上，提升序列 $Y$ 的连续性。然而，提升序列 $Y$ 的连续性，并不代表引入了光滑性，即连续性有限。换言之，序列 $Y$ 更像是一个 $C^0$ 函数，而非是一个 $C^1、C^2$ 乃至一个更高阶连续性的函数。

思想如此简单，但是为什么不去提升序列 $Y$ 的“导数”的连续性呢？（“ 泼天的富贵 “怎么能砸到我头上呢？）

困境在于序列“导数”或者称之为序列差分的性能太低。一方面，传统的前向、后向和中心差分均对噪声敏感，且所得差分序列的信噪比（SNR）更低。因此，对噪声差分序列进行平滑处理比直接对给定噪声信号进行平滑处理更为困难。另一方面，传统的去噪差分算法（如卷积 LoG 算子，卷积高斯一阶导数算子）会对“变化率表征”造成失真，此时再平滑差分序列，那么原始信号失真更多，这样的去噪效能不尽如人意。幸运的是，TGD 可作为离散信号良好的导数表征，在理论部分我们已经看到了其通过扩展了计算区间从而具备了一定的抗噪能力，并且从定性角度看很少失真。

有了全变分去噪算法打底，基于 TGD 的去噪算法就很简单得到了。

1.2 基于 TGD 的信号去噪算法

基于 TGD 的信号去噪算法很简单，可以通过最小化下列损失函数来得到：

$\begin{array}{rl}\underset{Y\in {\mathbb{R}}^N}{\mathrm{minimize}}({\lambda }_{\mathrm{offset}}\sum _{i=1}^N(Y[i]-X[i]{)}^2& +{\lambda }_{1\mathrm{st}}{\left(\sum _{i=1}^{N-1}{\left|Y_{\mathrm{TGD}}^{\prime }[i+1]-Y_{\mathrm{TGD}}^{\prime }[i]\right|}^p\right)}^{\frac{1}{p}}\\ & +{\lambda }_{2\mathrm{nd}}{\left(\sum _{i=1}^{N-1}{\left|Y_{\mathrm{TGD}}^{\prime \prime }[i+1]-Y_{\mathrm{TGD}}^{\prime \prime }[i]\right|}^p\right)}^{\frac{1}{p}}\end{array}$

损失函数一共有三部分组成。第一部分为 ${\sum }_{i=1}^N(Y[i]-X[i]{)}^2$ ，称为相似性损失，指得到的去噪序列和原始带噪序列需要保有一定的相似性， $Y$ 是源自 $X$ 的，不能差别太大。损失函数的第二部分 ${\left({\sum }_{i=1}^{N-1}|Y_{TGD}^{\prime }[i+1]-Y_{TGD}^{\prime }[i]{|}^p\right)}^{\frac{1}{p}}$ 称为一阶连续性损失，是对序列 $Y$ 的一阶 TGD 连续性的刻画，损失函数的第三部分 ${\left({\sum }_{i=1}^{N-1}|Y_{TGD}^{\prime \prime }[i+1]-Y_{TGD}^{\prime \prime }[i]{|}^p\right)}^{\frac{1}{p}}$ 称为二阶连续性损失，是对序列 $Y$ 的二阶 TGD 连续性的刻画。 ${\lambda }_{\mathrm{offset}}$ 、 ${\lambda }_{1\mathrm{st}}$ 和 ${\lambda }_{2\mathrm{nd}}$ 分别是正则化系数（也称为损失因子（loss factor）），当 ${\lambda }_{1\mathrm{st}}>0$ 且 ${\lambda }_{2\mathrm{nd}}=0$ ，表示只考虑序列 $Y$ 的一阶 TGD，近似得到一个 $C^1$ 函数；当 ${\lambda }_{2\mathrm{nd}}>0$ 时，则近似得到一个 $C^2$ 函数。并且 $Y_{TGD}^{\prime }=conv(Y,\hat{T})$ ， $Y_{TGD}^{\prime \prime }=conv(Y,\hat{R})$ ，其中 $\hat{T}$ 为一阶离散 TGD 算子， $\hat{R}$ 为二阶离散 TGD 算子，详见 TGD 第六篇：落地——离散序列的 TGD 计算。

TGD 的信号去噪算法，是一个非凸优化问题，但是仅包含“卷积”计算和最小化损失函数，为此 我们可以通过一层单层神经网络就实现 了。具体而言，初始化可学习的参数矩阵 $Y=X$ ，将离散 TGD 算子固定到单层卷积层的不可学习权重参数中，将 $Y$ 传递给卷积层之后就得到其 TGD 序列，然后计算损失，反向传播即可。下图展示了基于 TGD 的信号去噪算法示意图：

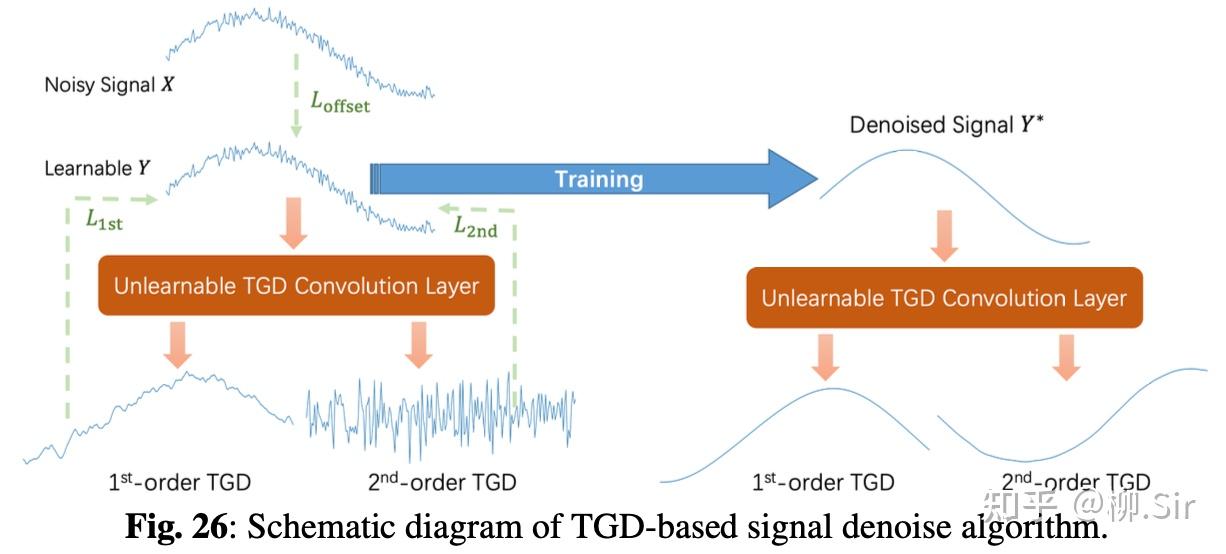
示意代码 如下：

import torch
from torch import nn
from torch.autograd import Variable
from torch.optim import Adam

TGDparam51 = {
    "TGDweigths": [
                   [[ 0.00098229,  0.00141411,  0.0020057 ,  0.00280279,  0.00385883,
                      0.00523435,  0.00699537,  0.00921085,  0.01194895,  0.01527218,
                      0.01923152,  0.02385982,  0.029165  ,  0.03512351,  0.04167493,
                      0.0487184 ,  0.05611156,  0.06367262,  0.07118595,  0.07841099,
                      0.08509435,  0.09098413,  0.09584549,  0.09947612,  0.10172019,
                      0.        , -0.10172019, -0.09947612, -0.09584549, -0.09098413,
                     -0.08509435, -0.07841099, -0.07118595, -0.06367262, -0.05611156,
                     -0.0487184 , -0.04167493, -0.03512351, -0.029165  , -0.02385982,
                     -0.01923152, -0.01527218, -0.01194895, -0.00921085, -0.00699537,
                     -0.00523435, -0.00385883, -0.00280279, -0.0020057 , -0.00141411,
                     -0.00098229]],
                   [[ 0.00098229,  0.00141411,  0.0020057 ,  0.00280279,  0.00385883,
                      0.00523435,  0.00699537,  0.00921085,  0.01194895,  0.01527218,
                      0.01923152,  0.02385982,  0.029165  ,  0.03512351,  0.04167493,
                      0.0487184 ,  0.05611156,  0.06367262,  0.07118595,  0.07841099,
                      0.08509435,  0.09098413,  0.09584549,  0.09947612,  0.10172019,
                      -2.       ,  0.10172019,  0.09947612,  0.09584549,  0.09098413,
                      0.08509435,  0.07841099,  0.07118595,  0.06367262,  0.05611156,
                      0.0487184 ,  0.04167493,  0.03512351,  0.029165  ,  0.02385982,
                      0.01923152,  0.01527218,  0.01194895,  0.00921085,  0.00699537,
                      0.00523435,  0.00385883,  0.00280279,  0.0020057 ,  0.00141411,
                      0.00098229]],
                ],
    "TGD1st_num": 1,        # 用了 1 个一阶离散 TGD 算子
    "TGD2nd_num": 1,        # 用了 1 个二阶离散 TGD 算子 
    "kernel_size": 51,      # 离散 TGD 算子尺寸
    "padding": 25,
    "lossFactor": [1, 10],  # lambda_1st 和 lambda_2nd
}


class TGDDenoiseNet(nn.Module):
    def __init__(self, init_seq = [], TGDparam = TGDparam51):
        super(TGDDenoiseNet, self).__init__()
        
        self.TGDparam = TGDparam # TGD 离散算子信息
        self.TGD1st_num = self.TGDparam["TGD1st_num"]  # 用了几个一阶 TGD 离散 TGD 算子，可以用多个
        self.TGD2nd_num = self.TGDparam["TGD2nd_num"]  # 用了几个二阶 TGD 离散 TGD 算子，可以用多个

        self.len = len(init_seq) # 带噪序列长度
        
        # 初始化可学习序列以及不可学习的卷积层
        temp_seq = [[init_seq]]
        self.init_seq = nn.Parameter(torch.FloatTensor(temp_seq), requires_grad=False)   # 带噪信号
        self.denoise_seq = nn.Parameter(torch.FloatTensor(temp_seq), requires_grad=True) # 去噪信号
        self.conv1 = nn.Conv1d(in_channels = 1, out_channels = self.TGD1st_num + self.TGD2nd_num, kernel_size = self.TGDparam["kernel_size"], stride = 1, padding = self.TGDparam["padding"], padding_mode = "replicate", bias=None)
        self.conv1.weight = nn.Parameter(torch.FloatTensor(self.param["TGDweigths"]), requires_grad=False) # 卷积层参数不可变

    def forward(self):
        return self.conv1(self.denoise_seq)

    def calTGD(self, seq):
        return self.conv1(seq)
    
    def calLoss(self, final_TGDseq, lambda_offset = 1, p = 2):
        res = torch.FloatTensor([0])
        for i in range(self.TGD1st_num):
            res = res + torch.sum(torch.norm(final_TGDseq[0][i][:-1] - final_TGDseq[0][i][1:], p = p, dim=0, keepdim=True)) * self.TGDparam["lossFactor"][i]
        for i in range(self.TGD1st_num, self.TGD1st_num + self.TGD2nd_num):
            res = res + torch.sum(torch.norm(final_TGDseq[0][i][:-1] - final_TGDseq[0][i][1:], p = p, dim=0, keepdim=True)) * self.TGDparam["lossFactor"][i]
        res = res + torch.sum(torch.pow((self.init_seq[0][0] - self.insert_seq[0][0]), 2)) * lambda_offset  # lambda_offset 为去噪序列 Y 和初始带噪序列 X 之间相似度损失的损失因子
        return res


denoisenet = TGDDenoiseNet(init_seq = ......., TGDparam = TGDparam51)
optimizer = Adam(filter(lambda p: p.requires_grad, denoisenet.parameters()), lr = 0.01)
torch.optim.lr_scheduler.StepLR(optimizer, step_size = 10000, gamma = 0.1)
epochs = 100000
for epoch in tqdm(range(epochs + 1)):
        optimizer.zero_grad()       # 将梯度置0
        final_TGDseq = denoisenet()
        loss = denoisenet.calLoss(final_TGDseq, lambda_offset = 0.01, p = 2) 
        loss.backward()             # 反向传播
        optimizer.step()            # 梯度的更新

1.3 实验结果及分析

1.3.1 定性分析

实验使用的两个带噪离散序列如下，其中 $\delta$ 表示噪声：

$\begin{array}{r}{X}_1(n)=20\sin \left(\frac{n}{40}\right)+\frac{n^2}{20000}+\delta (n),n=0,1,\dots ,1000\\ X_2(n)=\arctan \left(\frac{n-500}{40}\right)+\frac{n^2}{20000}+\delta (n),n=0,1,\dots ,1000\end{array}$

首先明确后续实验中使用的一阶和二阶离散 TGD 算子尺寸为 $51$ （我还没见过这么大尺寸的差分算子），如下图所示，具体数值在上面的示例代码中已经体现了；损失因子 ${\lambda }_{\mathrm{offset}}=0.01$ 、 ${\lambda }_{1\mathrm{st}}=1$ 、 ${\lambda }_{2\mathrm{nd}}=10$ ，使用 Adam 优化器，学习率为 $0.01$ 。具体的实验详情可直接阅读原始论文。

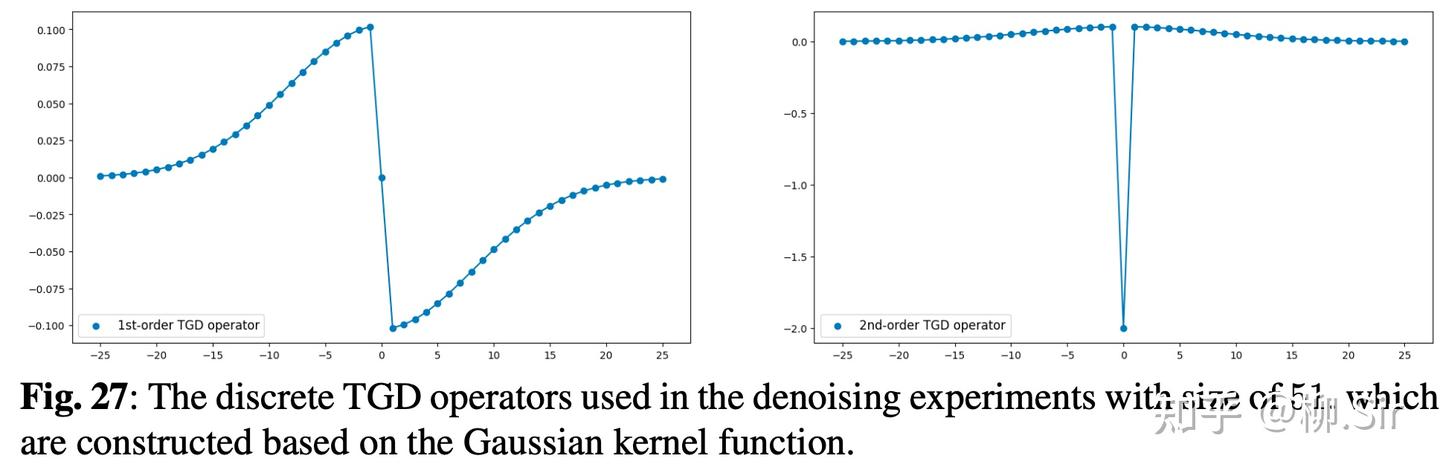
下图分别展示了带噪序列 $X_1$ 和 $X_2$ 的去噪过程第一列为去噪序列；第二列为去噪序列的一阶 TGD；第三列为去噪序列的二阶 TGD：

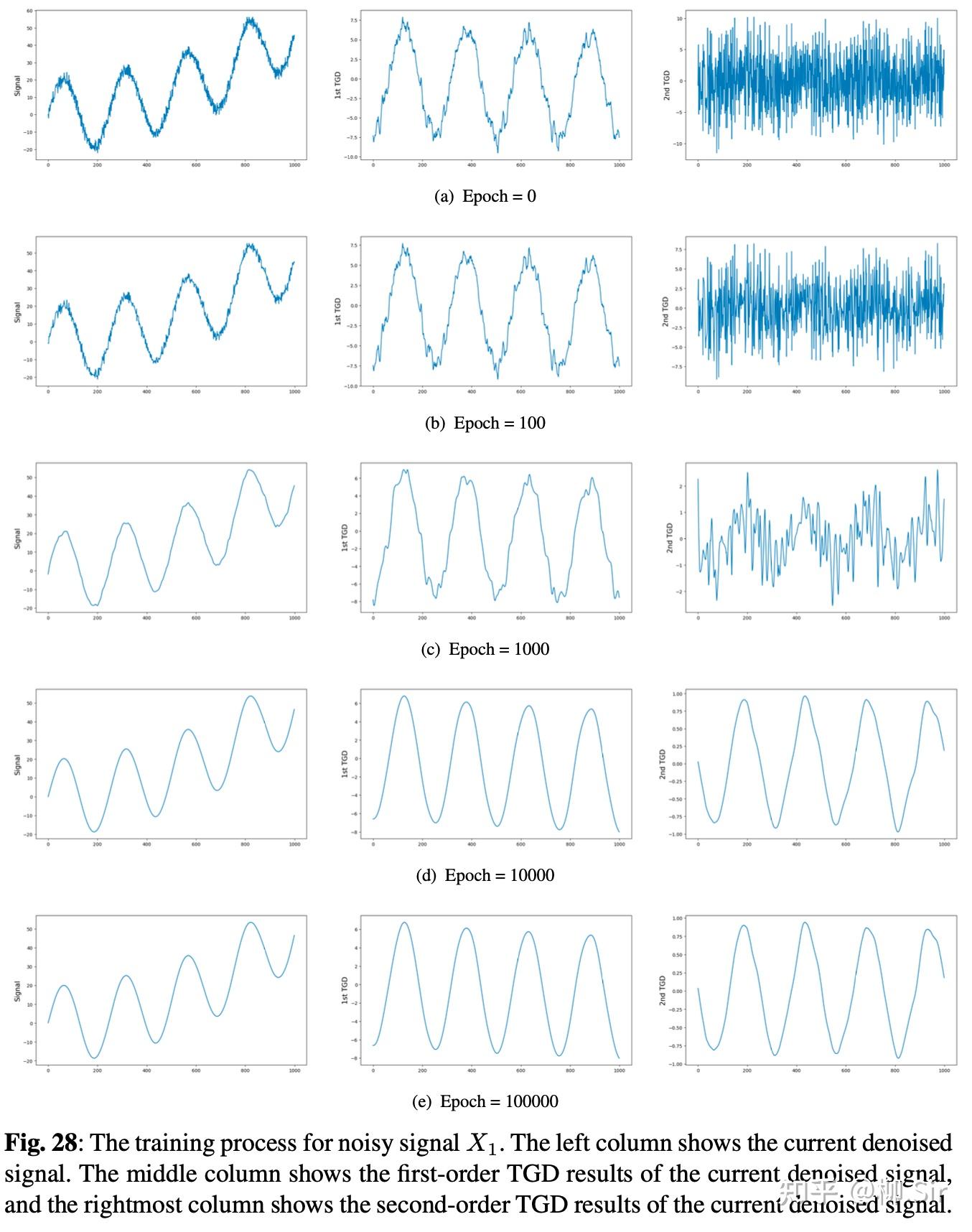
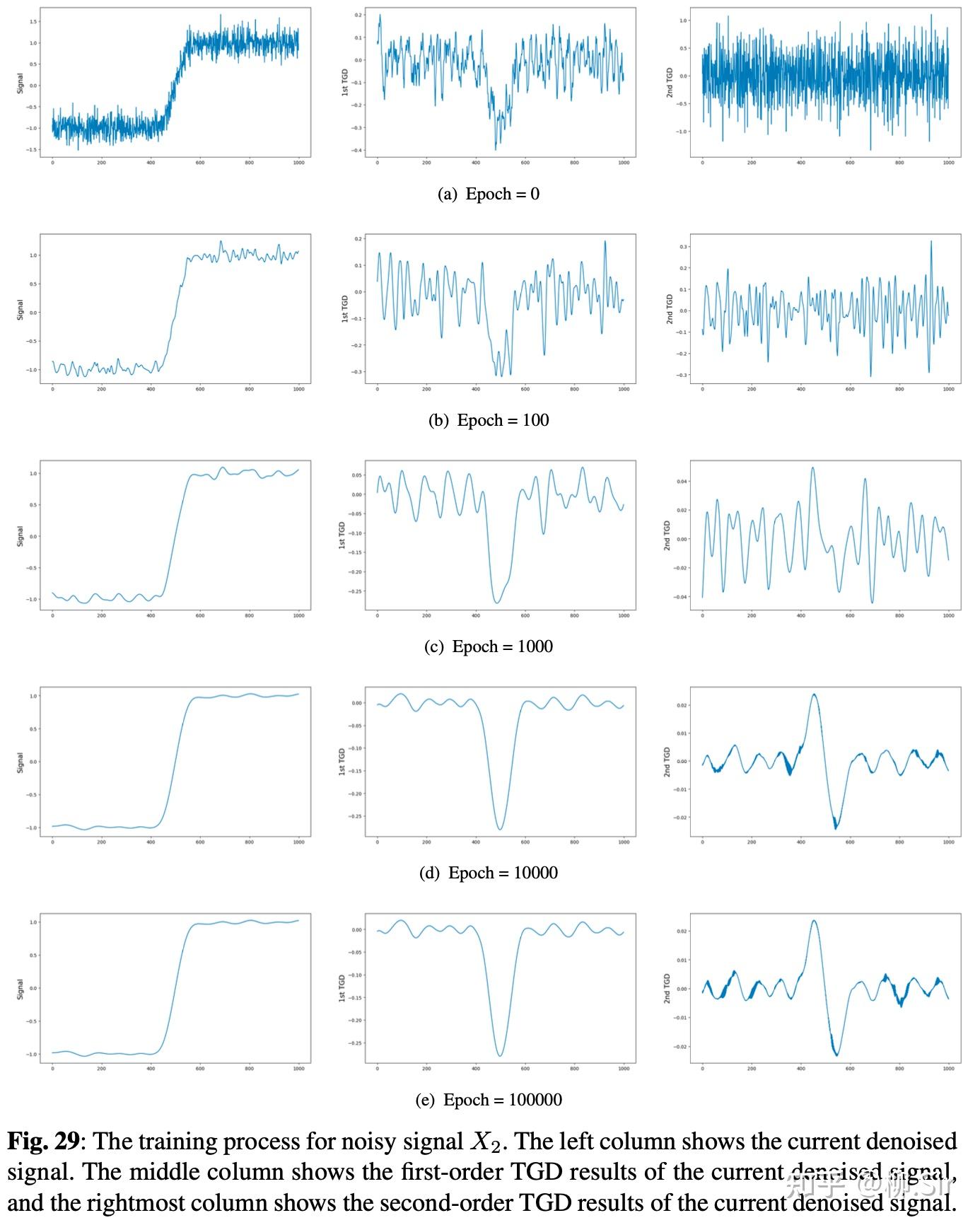
从第一行的噪声序列，到最后一行的去噪序列，效果还是很拔群的！

依然是针对带噪序列 $X_1$ 和 $X_2$ ，我分别施加不同强度的均匀噪声和高斯噪声的实验结果如下所示，橙色曲线表示理论上的无噪 Ground Truth，灰色虚线表示添加噪声后的信号，红色虚线表示基于 TGD 的去噪算法得到的结果。噪声特别强，强到信噪比 SNR 几乎为 $0$ 的极端情况下，基于 TGD 的去噪算法在不知道 Ground Truth，并且没有对原始信号做任何形式假设的背景下，仍然得到了很好的结果，体现了算法的通用性，以及高强的性能（泼天的富贵真的被我接住了）。

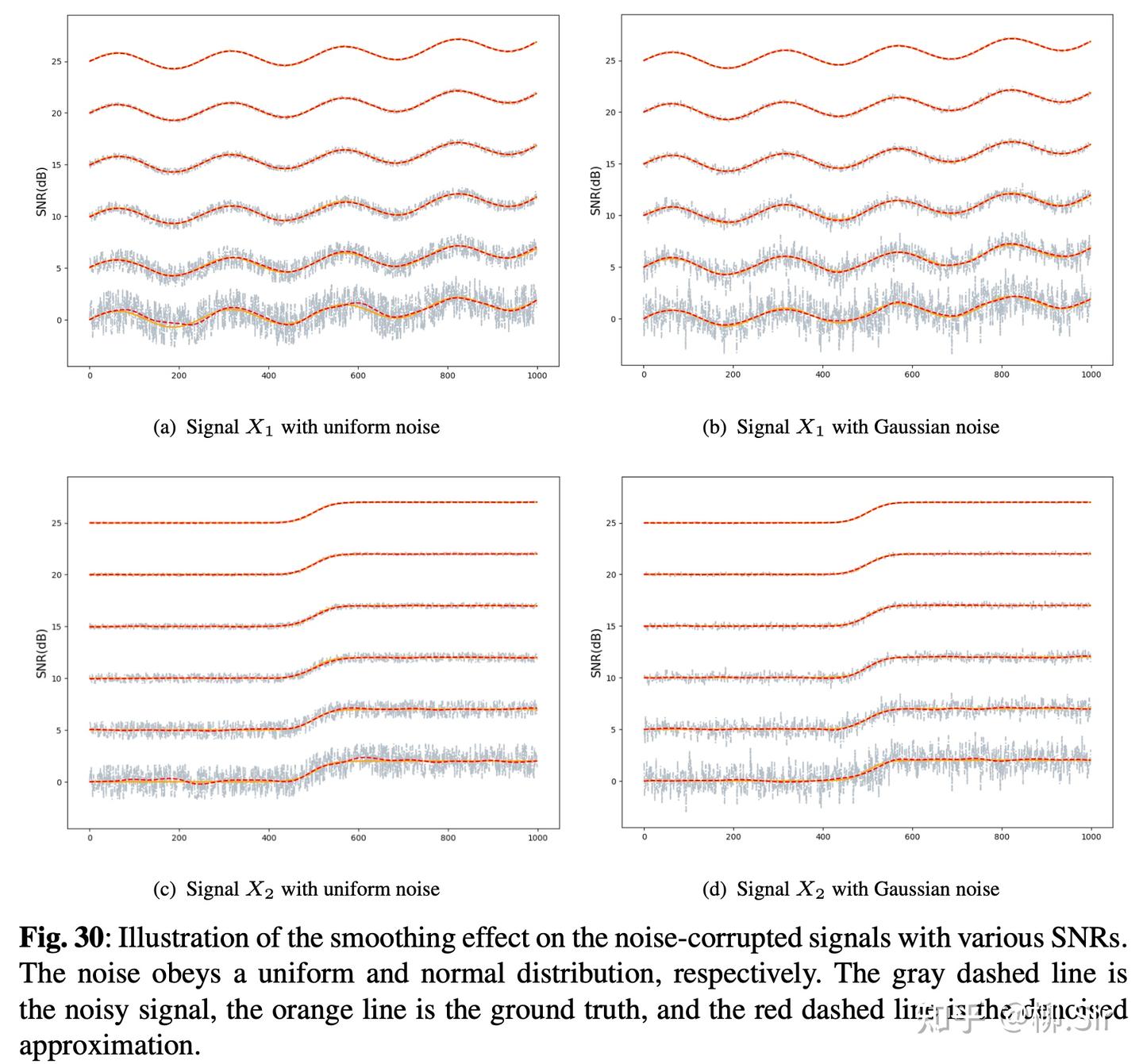
1.3.2 定量分析

定量分析中，我使用了三个指标：RMSE（均方根误差），PSNR（峰值信噪比），SSIM（结构相似度）。对比的去噪算法包括：高斯平滑去噪、小波去噪、全变分去噪（https://github.com/MrCredulous/1D-MCTV-Denoising）、SVD去噪算法（https://github.com/nerdull/denoise/blob/master/denoise.py）。2020年10月的SVD去噪算法论文和TGD去噪算法稍微能打一下，其他的都不太行。

依然针对序列 $X_1$ 和 $X_2$ ，分别添加方差为 $2$ 和 $0.2$ 的高斯噪声。量化指标如下所示：

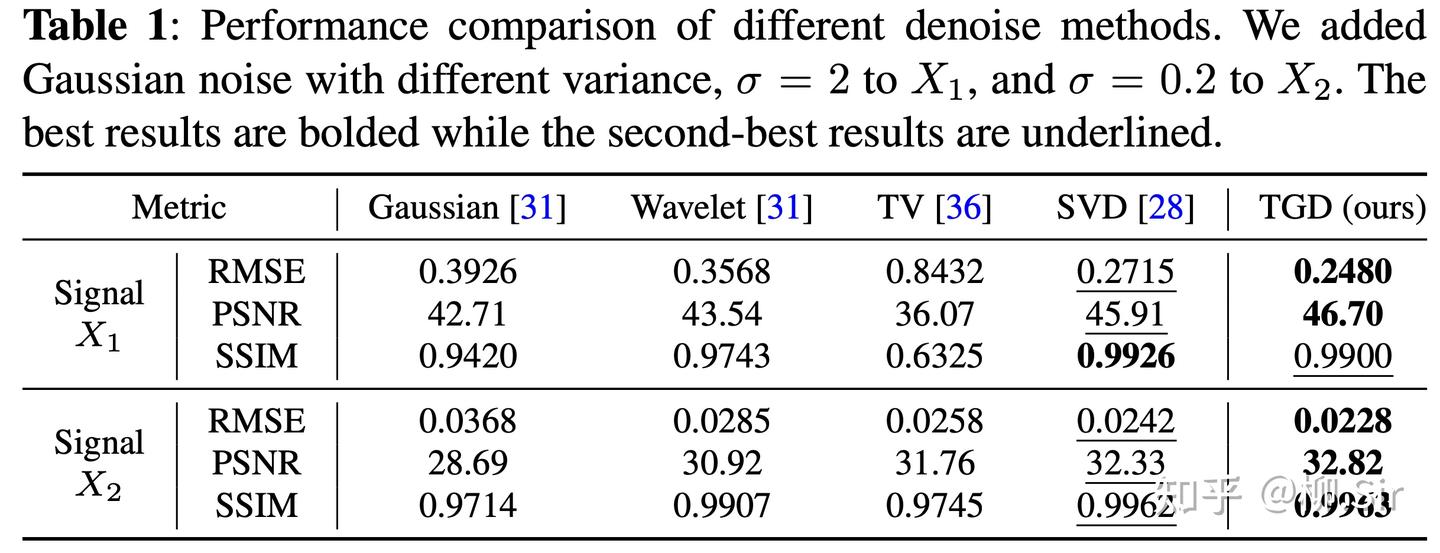
下图分别展示了针对带噪序列 $X_1$ 和 $X_2$ 的去噪对比，第一行分别展示了 Ground Truth 和带噪信号；第二行为去噪信号；第三行为去噪信号的一阶 TGD；第四行为去噪信号的二阶 TGD。

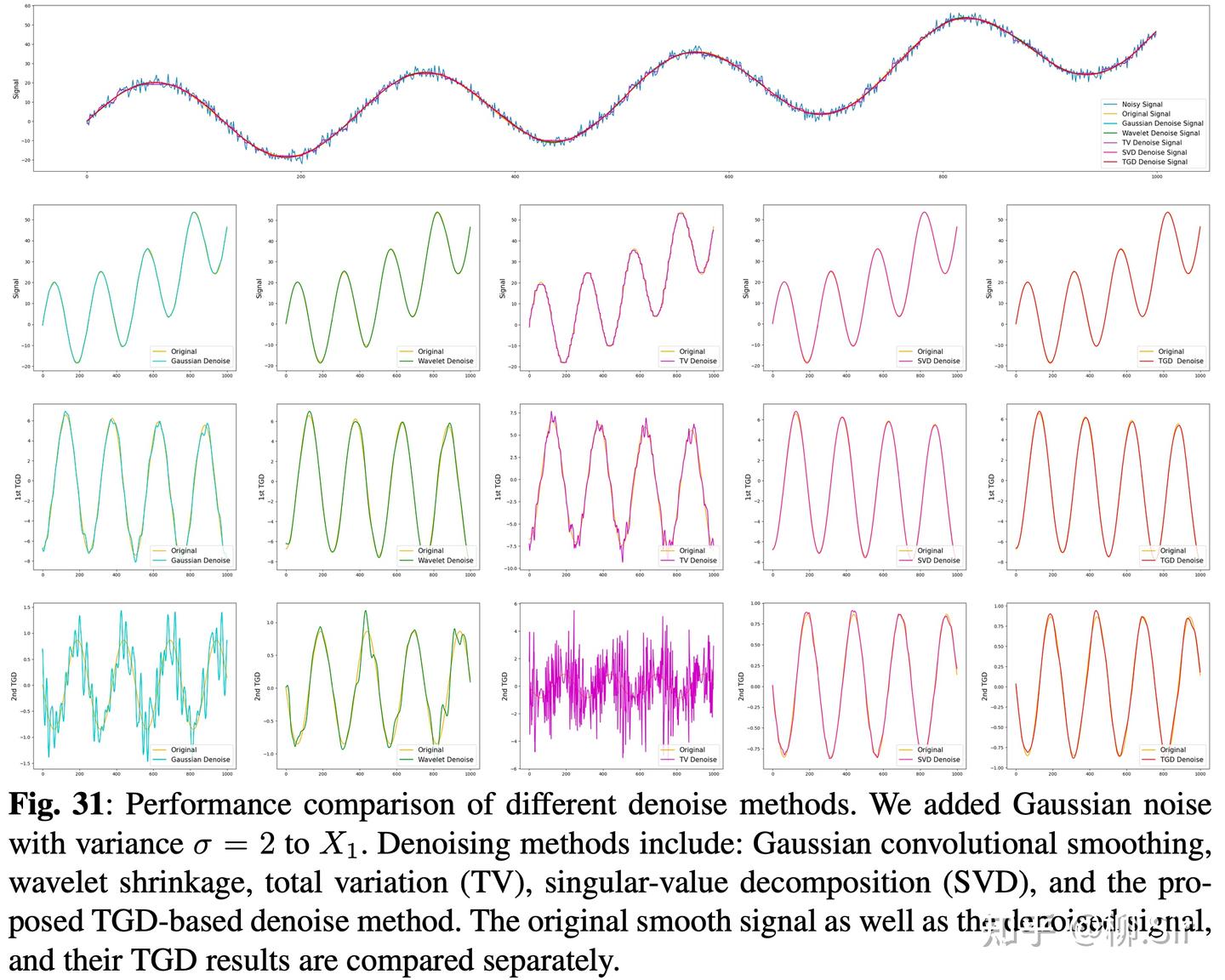
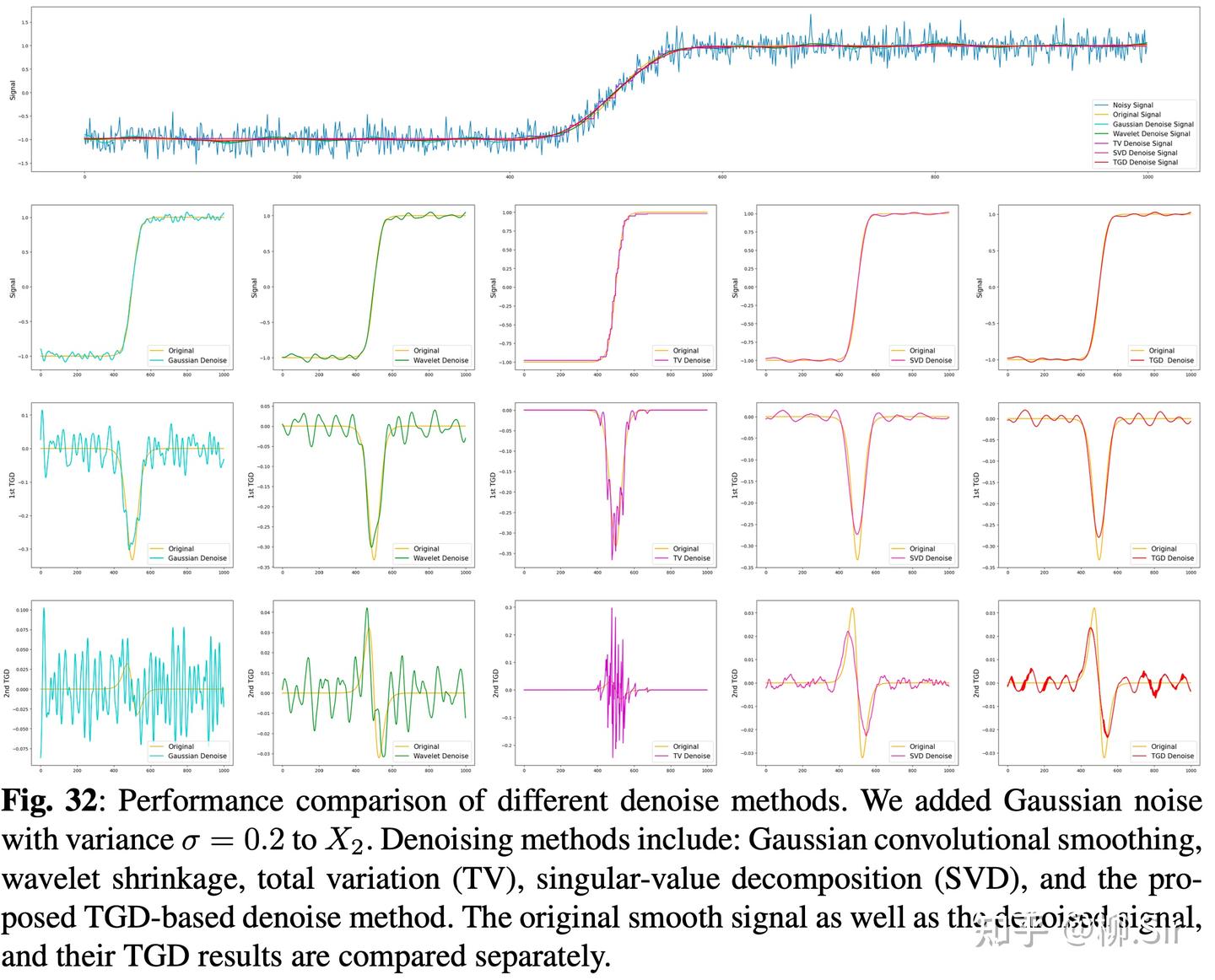
1.3.3 消融实验

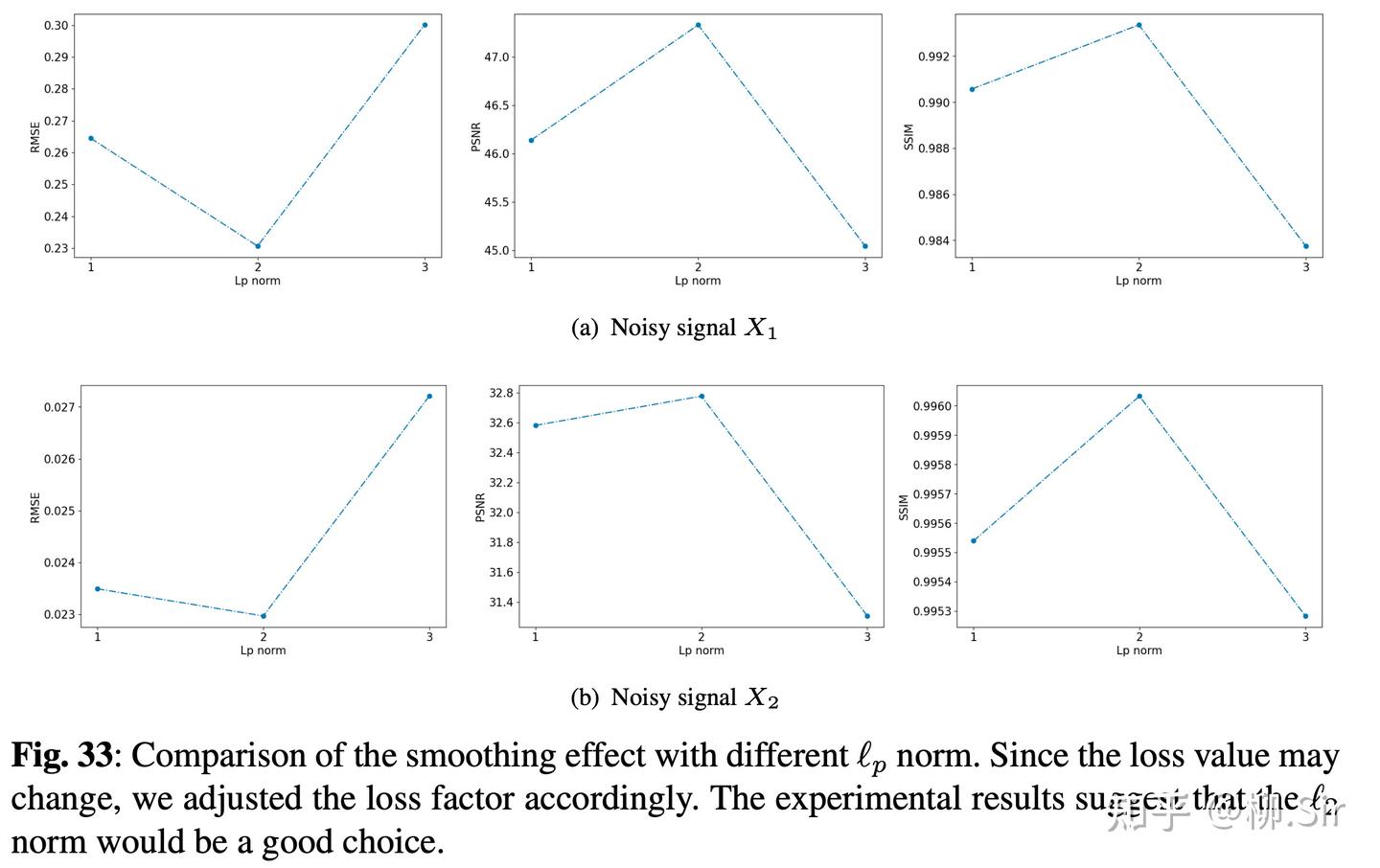
第一个消融实验对不同范数刻画联系性进行比较。结果显示 $p=2$ ，即连续性用 ${\ell }_2$ 范数度量比较好。

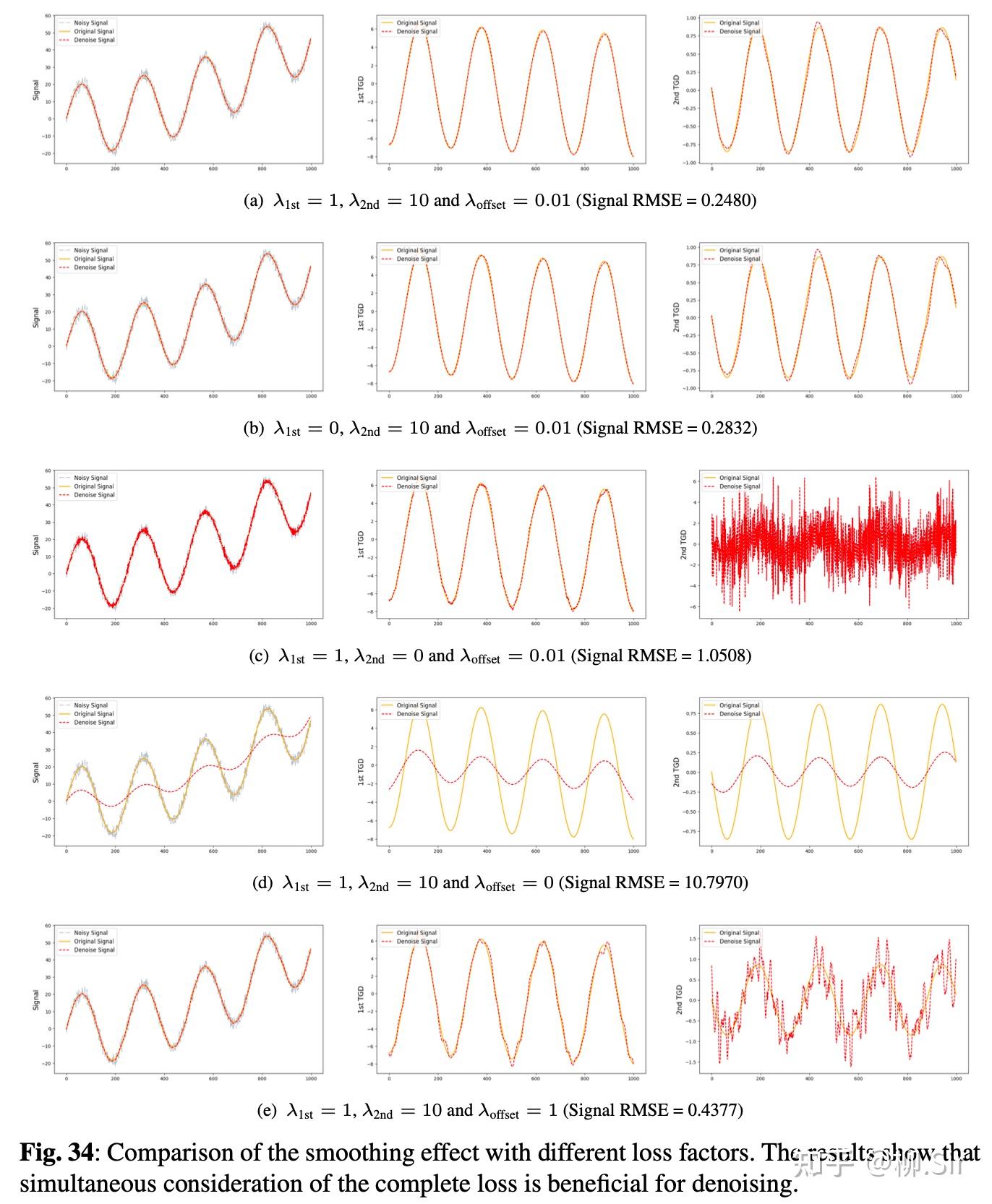
第二个消融实验对损失因子进行比较。当 ${\lambda }_{2\mathrm{nd}}=0$ 时（第三行），表示不对二阶TGD连续性进行约束，明显看出去噪序列的一阶TGD还算连续，但是二阶TGD惨不忍睹；当 ${\lambda }_{\mathrm{offset}}=0$ 时（第四行），表示不对去噪信号和原始信号之间的相似度进行约束，为了使得损失函数最小，一阶和二阶TGD均会进行幅度收缩，最终造成噪声幅度收缩，产生信号“失真”；当 ${\lambda }_{\mathrm{offset}}$ 比较大时（第五行），会一定程度上损失一阶和二阶TGD的连续性。最后表明，适当合理的分配三个损失因子，会得到更好的结果。

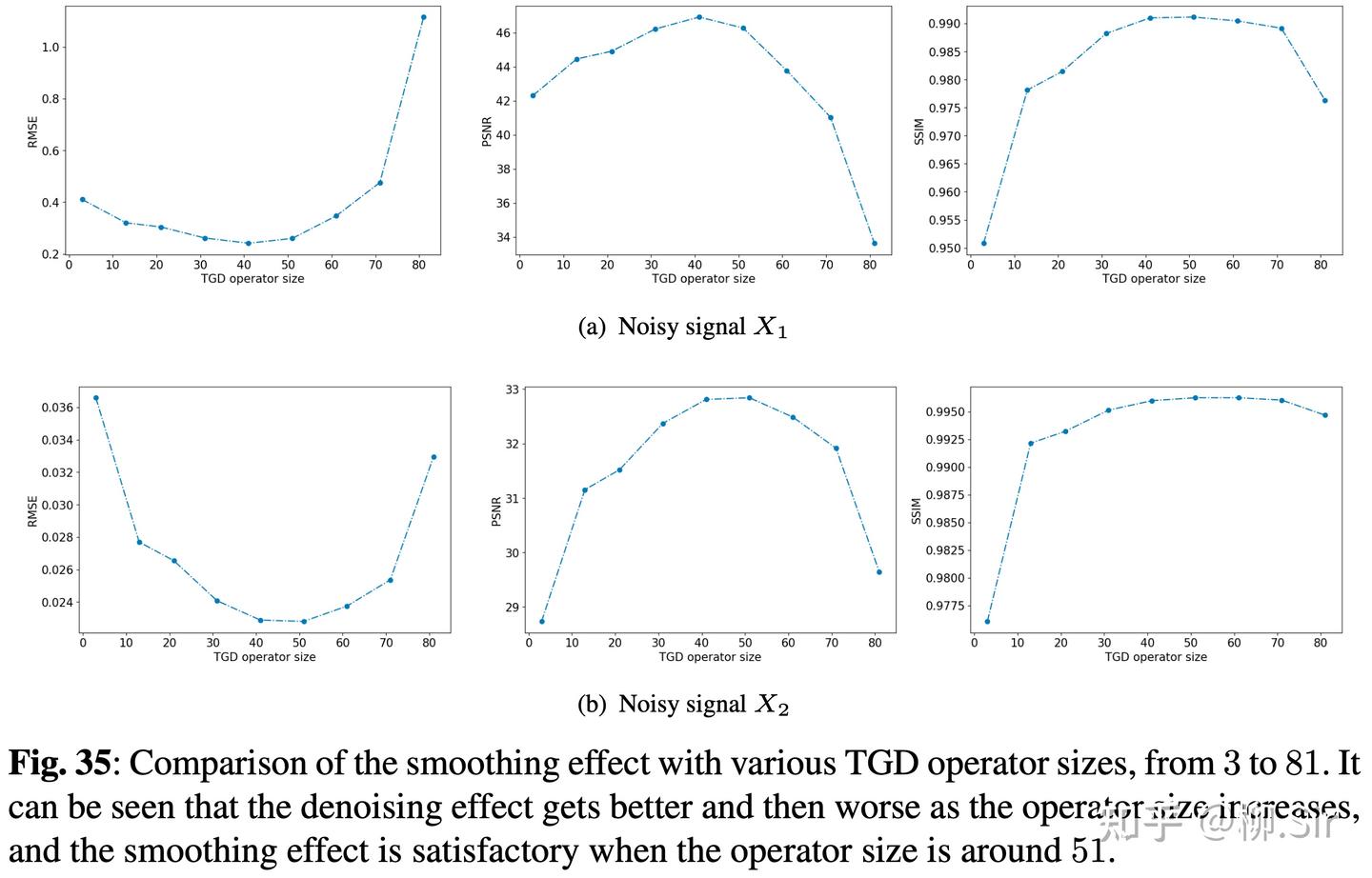
第三个消融实验对TGD算子尺寸进行比较，注意到信号序列长度为1000，实验结论和“预期”保持一致，即算子尺寸过大过小都会损害性能，算子尺寸过小，去噪性能有限；算子尺寸过大，平滑过度会有一定的失真，去噪性能也会下降。应该说，算子大小随着信号序列长度增加，合理增大，是一个比较好的处理模式。

二、基于TGD的信号插值算法

去噪和插值是一个任务吗？有人或许有这个疑问，但是如果我说，“基于TGD的信号去噪算法可以很容易的扩展为带噪信号的插值算法呢”？阁下当如何应对 。

2.1 基于TGD的信号去噪算法变形

信号插值依然建立在「 平滑假设 」之上，即“离散信号是由光滑函数上采样得到的一系列实数值（是减少数据量），插值像是采样的逆向操作，即增加离散信号的数据量，将近似去恢复出该光滑函数”。

在TGD 第六篇中我们提出了离散序列转变为连续函数的方法： 将离散序列拟合为一个阶梯函数 。那么，如果我提升该阶梯函数的TGD的连续性，不就可以得到一个插值后的光滑函数了吗！

那么，“基于TGD的信号去噪算法”按如下形式进行修改，就可以得到“基于TGD的信号插值算法”，其中 $X$ 为初始序列进行阶梯函数形式插值后的新初始序列， $Y$ 为最终的插值序列；Mask 为掩码序列，其在初始采样点的位置值为 $1$ ，插值位置值为 $0$ 。（备注：初始序列也可以通过线性插值、三次样条插值等进行初始化…，为了和其他插值算法结果做比较，我就做了方便算法收敛的最不算插值的插值，即阶梯函数形式的插值；直接插 $0$ 也简单，但是不一定方便算法收敛）

$\begin{array}{rl}\underset{Y\in {\mathbb{R}}^N}{\mathrm{minimize}}({\lambda }_{\mathrm{offset}}\sum _{i=1}^N(（Y[i]-X[i])\times \mathrm{Mask}[i]{)}^2& +{\lambda }_{1\mathrm{st}}{\left(\sum _{i=1}^{N-1}{\left|Y_{\mathrm{TGD}}^{\prime }[i+1]-Y_{\mathrm{TGD}}^{\prime }[i]\right|}^p\right)}^{\frac{1}{p}}\\ & +{\lambda }_{2\mathrm{nd}}{\left(\sum _{i=1}^{N-1}{\left|Y_{\mathrm{TGD}}^{\prime \prime }[i+1]-Y_{\mathrm{TGD}}^{\prime \prime }[i]\right|}^p\right)}^{\frac{1}{p}}\end{array}$

此时，损失函数依然由三部分组成。第一部分为 ${\sum }_{i=1}^N((Y[i]-X[i])\times \mathrm{Mask}[i]{)}^2$ ，称为相似性损失，指得到的插值序列和原始序列在初始采样位置需要保有一定的相似性。损失函数的第二部分 ${\left({\sum }_{i=1}^{N-1}|Y_{TGD}^{\prime }[i+1]-Y_{TGD}^{\prime }[i]{|}^p\right)}^{\frac{1}{p}}$ 称为一阶连续性损失，是对插值后序列 $Y$ 的一阶 TGD 连续性的刻画，损失函数的第三部分 ${\left({\sum }_{i=1}^{N-1}|Y_{TGD}^{\prime \prime }[i+1]-Y_{TGD}^{\prime \prime }[i]{|}^p\right)}^{\frac{1}{p}}$ 称为二阶连续性损失，是对插值后序列 $Y$ 的二阶 TGD 连续性的刻画。

${\lambda }_{\mathrm{offset}}$ 、 ${\lambda }_{1\mathrm{st}}$ 和 ${\lambda }_{2\mathrm{nd}}$ 分别是正则化系数（也称为损失因子）。当 ${\lambda }_{\mathrm{offset}}$ 特别大时，表示不希望插值后序列在采样位置和原始采样值有差别，适用于无噪环境；当 ${\lambda }_{\mathrm{offset}}$ 不是特别大时，表示能容许插值后序列在采样位置和原始采样值有些许差别，适用于带噪环境。当 ${\lambda }_{1\mathrm{st}}>0$ 且 ${\lambda }_{2\mathrm{nd}}=0$ ，表示只考虑序列 $Y$ 的一阶 TGD，近似得到一个 $C^1$ 函数；当 ${\lambda }_{2\mathrm{nd}}>0$ 时，则近似得到一个 $C^2$ 函数。并且 $Y_{TGD}^{\prime }=conv(Y,\hat{T})$ ， $Y_{TGD}^{\prime \prime }=conv(Y,\hat{R})$ ，其中 $\hat{T}$ 为一阶离散 TGD 算子， $\hat{R}$ 为二阶离散 TGD 算子。

可见， 基于TGD的信号插值算法既适用于无噪环境，也适用于带噪环境 。

基于TGD的去噪算法，只是基于TGD的信号插值算法在带噪环境下，且两个采样点间需要插入 $0$ 个值时候的特例！

此外，据我所知（仅仅是据我所知而已，我的所知有限），与传统的基于分段拟合的插值算法不同，基于 TGD 的信号插值方法首次将整个离散序列作为一个整体加以考虑，并通过迭代优化损失函数从而获得整个最终的插值序列。

通过两个简单的例子可以对基于 TGD 的插值算法有效性进行初步认识。无噪环境下，当待插值的序列是一个常数序列（例如 $[1,1,\cdots ,1,1]$ ）时，基于 TGD 的信号插值算法会插入相同的常数值，因为只有常数序列的 TGD 结果总是 $0$ ，此时的损失也是 $0$ 。当需要插值的序列是一个线性序列（例如 $[1,2,\cdots ,8,9]$ ）时，基于 TGD 的信号插值算法将会进行线性插值，因为线性序列的 TGD 结果是一个常数值，此时的损失也是 $0$ 。

这里我就不给完整代码示例了，在之前的代码示例中，大家自行进行阶梯函数插值，然后作为TGDInsertNet的init_seq，并且新增一个对应与 init_seq 的 mask 掩码序列，略微修改 calLoss 函数即可。

TGDparam = {
     'TGDweigths': [
                   [[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
                      0.04296968,  0.07925519,  0.13058009,  0.19264741,  0.25423729,  0.30031034,  
                      0.        , -0.30031034, -0.25423729, -0.19264741, -0.13058009, -0.07925519, -0.04296968,
                      0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
                    ]],
                   [[  0.00165359,  0.00252103,  0.00376125,  0.00549156,  0.00784633,
                       0.010971  ,  0.01501178,  0.02010142,  0.02634079,  0.03377841,
                       0.04238937,  0.05205744,  0.06256281,  0.07357963,  0.08468506,
                       0.09538144,  0.10513047,  0.11339692,  0.11969657,  0.12364313,
                       0.        , -0.12364313, -0.11969657, -0.11339692, -0.10513047,
                      -0.09538144, -0.08468506, -0.07357963, -0.06256281, -0.05205744,
                      -0.04238937, -0.03377841, -0.02634079, -0.02010142, -0.01501178,
                      -0.010971  , -0.00784633, -0.00549156, -0.00376125, -0.00252103,
                      -0.00165359]],
                   [[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
                      0.04296968,  0.07925519,  0.13058009,  0.19264741,  0.25423729,  0.30031034,  
                     -2.0       ,  0.30031034,  0.25423729,  0.19264741,  0.13058009,  0.07925519,  0.04296968
                      0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
                    ]],
                   [[ 0.00165359,  0.00252103,  0.00376125,  0.00549156,  0.00784633,
                      0.010971  ,  0.01501178,  0.02010142,  0.02634079,  0.03377841,
                      0.04238937,  0.05205744,  0.06256281,  0.07357963,  0.08468506,
                      0.09538144,  0.10513047,  0.11339692,  0.11969657,  0.12364313,
                     -2.0       ,  0.12364313,  0.11969657,  0.11339692,  0.10513047,
                      0.09538144,  0.08468506,  0.07357963,  0.06256281,  0.05205744,
                      0.04238937,  0.03377841,  0.02634079,  0.02010142,  0.01501178,
                      0.010971  ,  0.00784633,  0.00549156,  0.00376125,  0.00252103,
                      0.00165359]],
                ],
    'TGD1st_num': 2,
    'TGD2nd_num': 2, 
    'kernel_size': 41,
    'padding': 20,
    'lossFactor': [1,1,10,10],
} 

class TGDInsertNet(nn.Module):
    def __init__(self, init_seq = [], mask_seq = [], TGDparam = TGDparam):
        super(TGDInsertNet, self).__init__()
        
        self.TGDparam = TGDparam    # TGD 离散算子信息
        self.TGD1st_num = self.TGDparam["TGD1st_num"]  # 用了几个一阶 TGD 离散 TGD 算子，可以用多个
        self.TGD2nd_num = self.TGDparam["TGD2nd_num"]  # 用了几个二阶 TGD 离散 TGD 算子，可以用多个
        
        # 掩码序列
        self.mask_seq = mask_seq    # 相邻采样点间插入4个新数据点的掩码序列如 [...,0,0,1,0,0,0,0,1,0,0,...]
        self.mask_seq = torch.tensor(self.mask_seq)

        self.len = len(init_seq)    # 插值后序列长度
        
        # 初始化可学习序列以及不可学习的卷积层
        temp_seq = [[init_seq]]
        self.init_seq = nn.Parameter(torch.FloatTensor(temp_seq), requires_grad=False)   # 初始插值的阶梯信号
        self.insert_seq = nn.Parameter(torch.FloatTensor(temp_seq), requires_grad=True)  # 插值后的信号
        self.conv1 = nn.Conv1d(in_channels = 1, out_channels = self.TGD1st_num + self.TGD2nd_num, kernel_size = self.TGDparam["kernel_size"], stride = 1, padding = self.TGDparam["padding"], padding_mode = "replicate", bias=None)
        self.conv1.weight = nn.Parameter(torch.FloatTensor(self.param["TGDweigths"]), requires_grad=False) # 卷积层参数不可变

    def forward(self):
        return self.conv1(self.insert_seq)

    def calTGD(self, seq):
        return self.conv1(seq)
    
    def calLoss(self, final_TGDseq, lambda_offset = 100, p = 2):
        res = torch.FloatTensor([0])
        for i in range(self.TGD1st_num):
            res = res + torch.sum(torch.norm(final_TGDseq[0][i][:-1] - final_TGDseq[0][i][1:], p = p, dim=0, keepdim=True)) * self.TGDparam["lossFactor"][i]
        for i in range(self.TGD1st_num, self.TGD1st_num + self.TGD2nd_num):
            res = res + torch.sum(torch.norm(final_TGDseq[0][i][:-1] - final_TGDseq[0][i][1:], p = p, dim=0, keepdim=True)) * self.TGDparam["lossFactor"][i]
        res = res + torch.sum(torch.pow((self.init_seq[0][0] * self.mask_seq - self.insert_seq[0][0] * self.mask_seq), 2)) * lambda_offset  # lambda_offset 为去噪序列 Y 和初始带噪序列 X 之间相似度损失的损失因子
        return res
 

2.2 无噪环境下基于TGD的信号插值

我用两个序列来进行展示，初始采样序列我分别采样了 $101$ 个点，要求在每两个给定的点之间插入 $10$ 个新的数据点：

$\begin{array}{l}{X}_1(n)=\tanh \left(\frac{n-50}{5}\right),n=0,1,\cdots ,100\\ X_2(n)=20\sin \left(\frac{n}{4}\right)+\frac{n^2}{200},n=0,1,\cdots ,100\end{array}$

在实验中，选择使用 Adam 优化器，学习率为 0.01。使用了两个尺寸分别为 13 和 41 的二阶 TGD 算子，其中尺寸为 13 的算子通过两端补 0 将尺寸拓展为 41，以便可以仅保留一个卷积层。至于损失因子，无噪情况下， ${\lambda }_{\mathrm{offset}}=100$ 、 ${\lambda }_{1\mathrm{st}}=0$ 、 ${\lambda }_{2\mathrm{nd}}=10$ （消融实验表明，无噪情况（理想环境）下，仅考虑二阶 TGD 的连续性就比较好了，因为理想环境下，二阶导数都连续了，那么一阶导数就光滑了）。

2.2.1 定性分析

无噪序列 $X_1$ 和 $X_2$ 的插值过程如下所示，第一列红色点为采样点，第一行展示了初始情况下插值的阶梯函数和对应的TGD值：

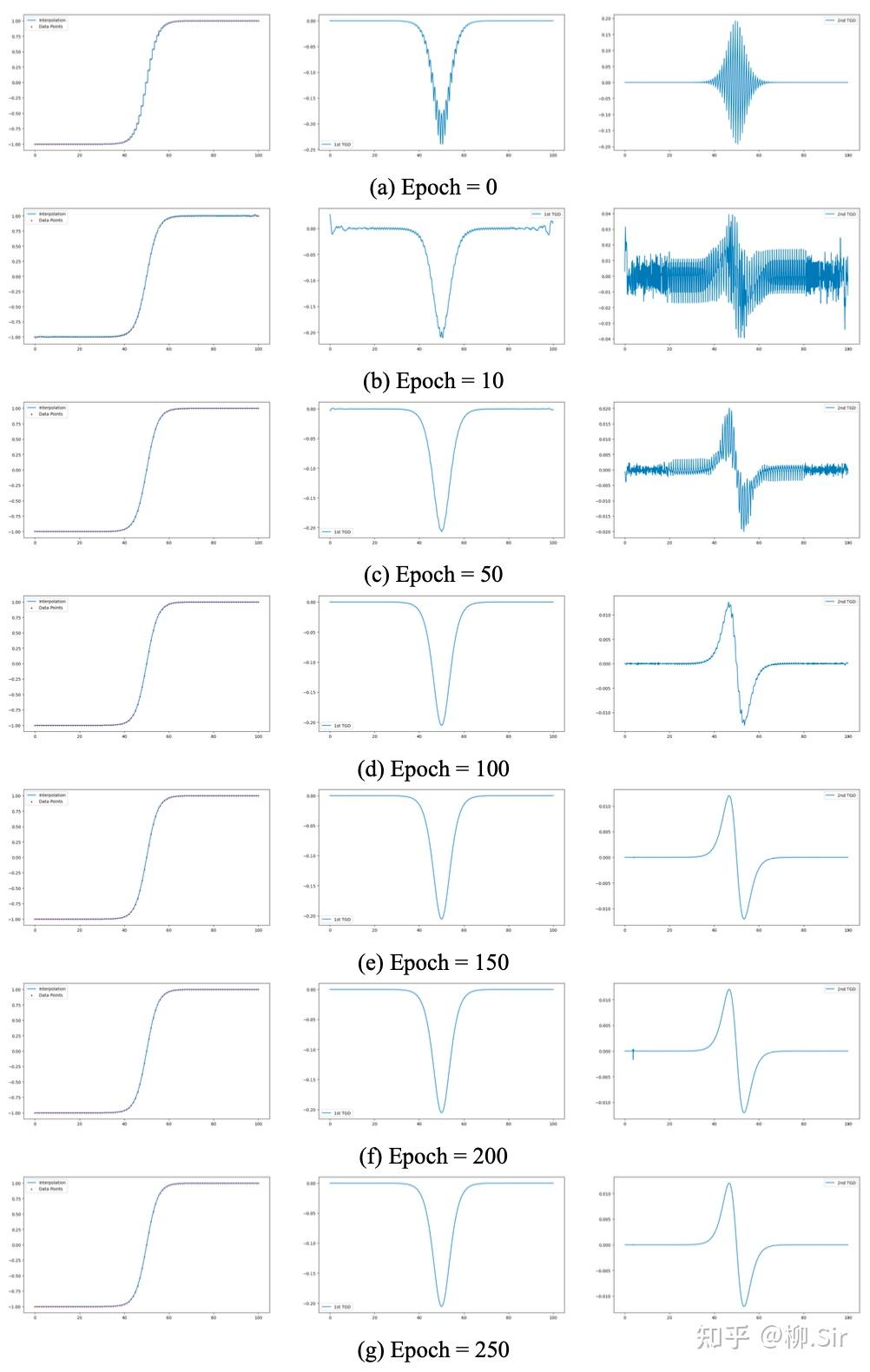
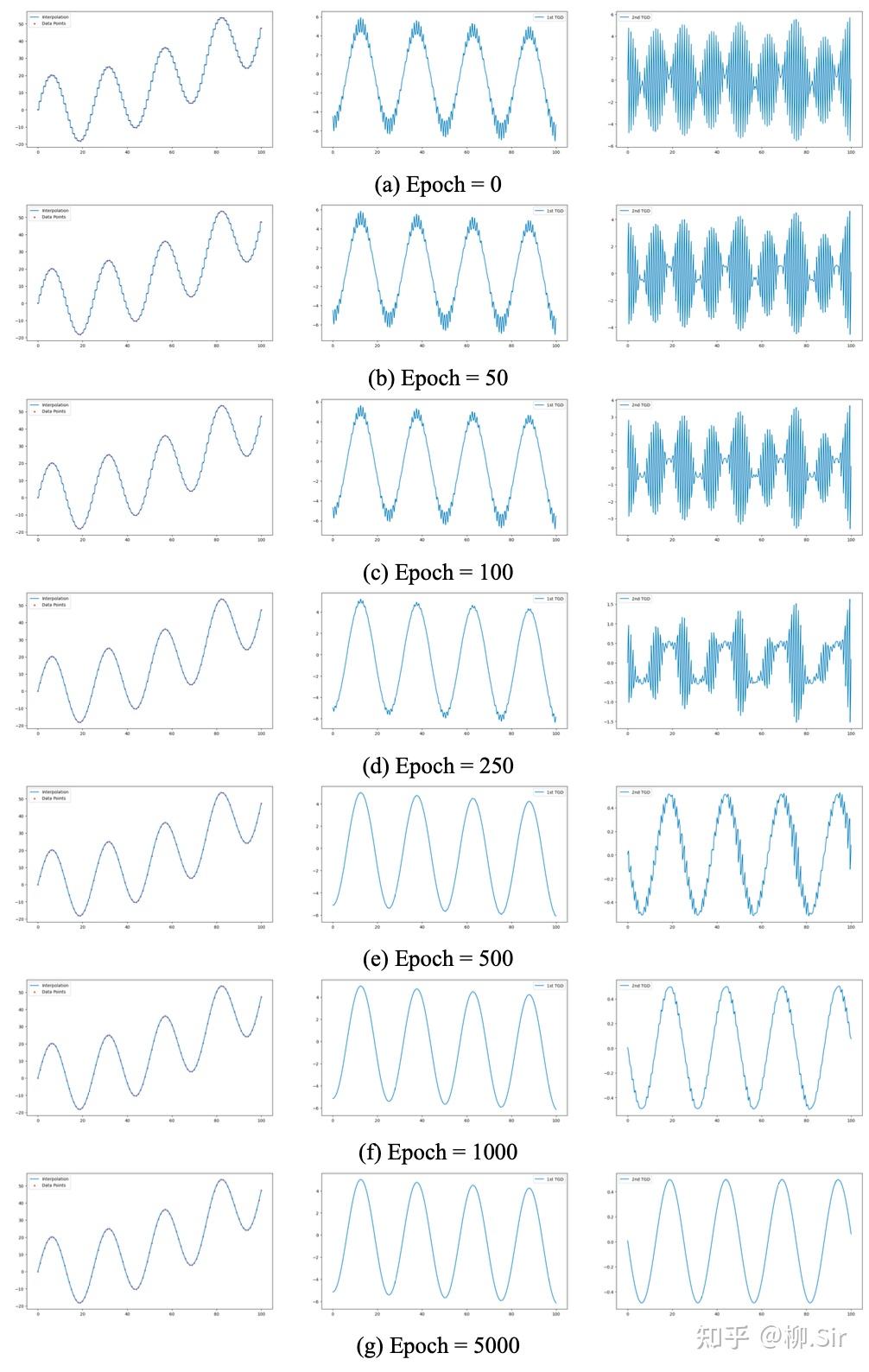
不同损失因子对无噪序列插值结果比较如下所示：第一行展示了当 ${\lambda }_{2\mathrm{nd}}=0$ 时，仅考虑一阶TGD的连续性，那么插值后序列的二阶TGD惨不忍睹，就像是一个 $C^1$ 函数；第二行展示了当 ${\lambda }_{1\mathrm{st}}=0$ 时，仅考虑二阶TGD的连续性，那么插值后序列的一阶和二阶TGD都不错，就像是一个 $C^2$ 函数，这与微积分中若函数 $f$ 为 $C^k$ 函数，则函数 $f$ 一定为 $C^{k-1}$ 函数的结论相一致；第三行则表明，在无噪的理想环境下，同时约束一阶和二阶TGD的连续性，由于是非凸优化问题，还可能会损失性能。因此， 建议在无噪声环境下仅考虑损失函数中的“相似性损失”和“二阶连续性损失”即可。

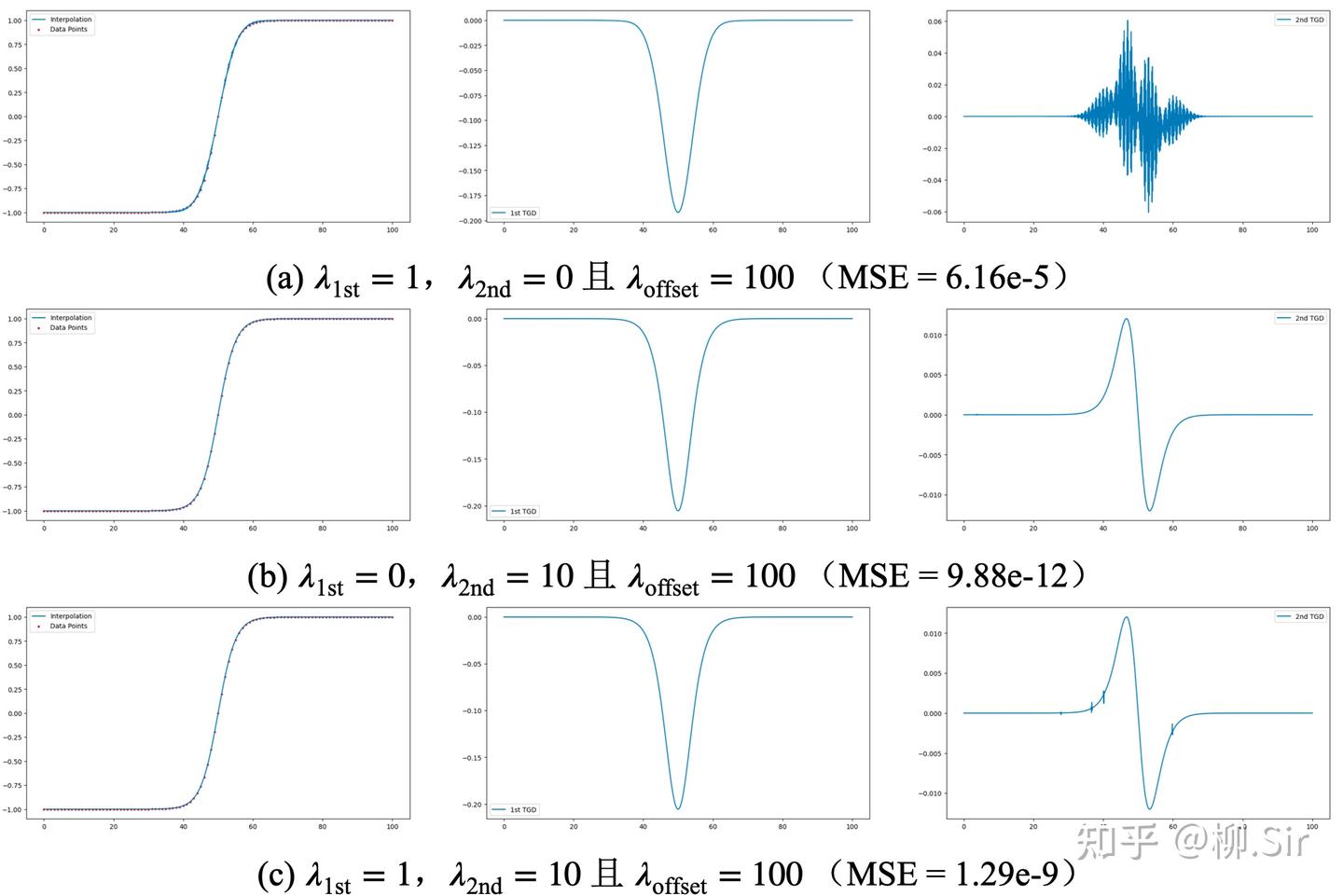
2.2.2 定量分析

现在将基于 TGD 的插值方法与传统基于分段拟合的插值方法进行比较，包括线性插值（Linear Interpolation）、二次样条插值（Quadratic Interpolation）和三次样条插值（Cubic Interpolation），这些方法使用 SciPy 插值模块（scipy.interpolate）进行实现。不同插值算法的定量分析比较如下所示：均方误差值越小表明插值效果越好，其中最好的结果用黑体表示，第二好的结果用下划线表示。在无噪声情况下，线性插值的表现最差，基于 TGD 的插值优于二次样条插值，而微弱于三次样条插值方法。由于 TGD 算法与其他分段拟合的插值算法在原理上有根本的不同，它在无噪声条件下的结果令人（至少令我）满意。

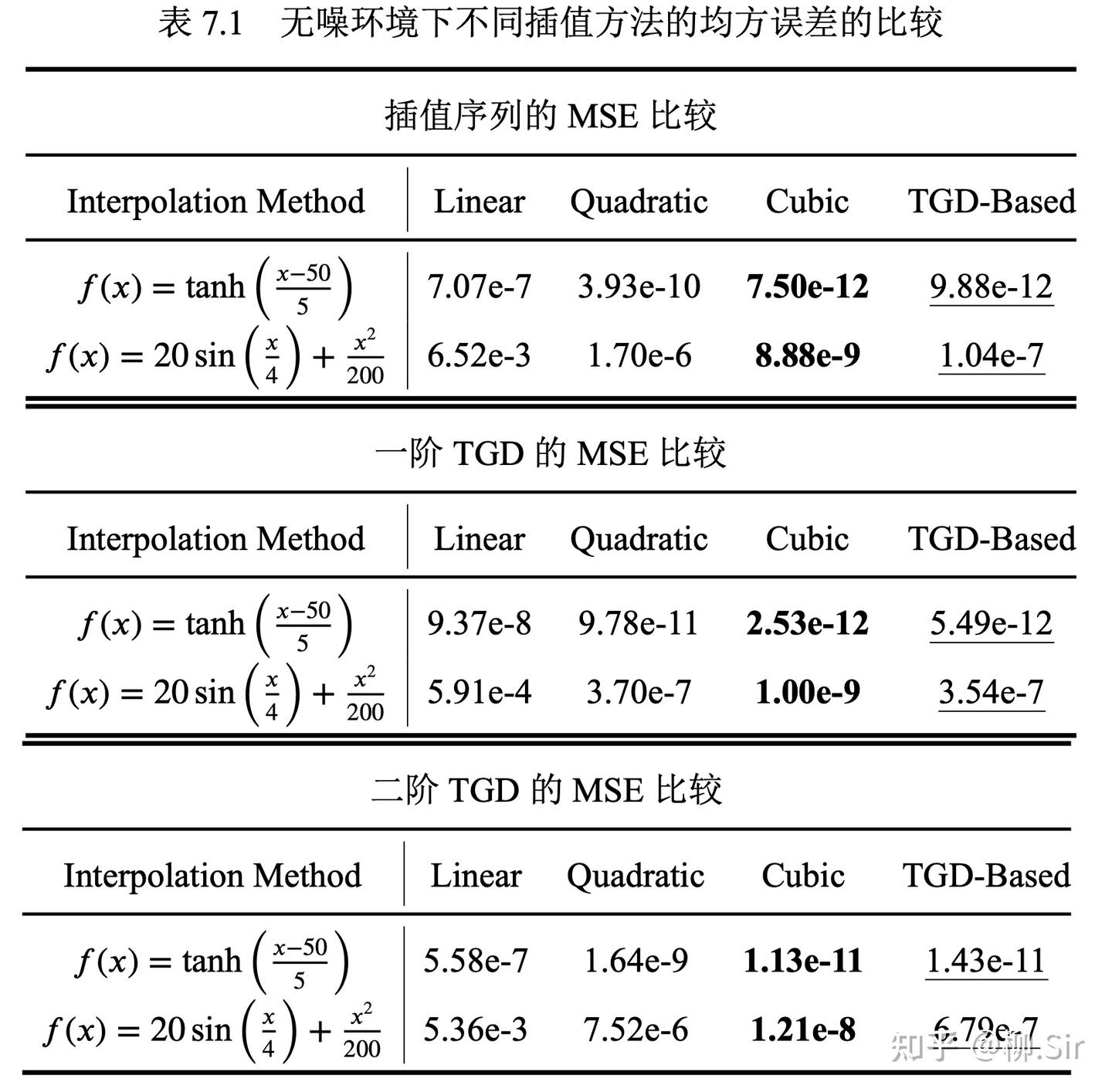
从下图中可见，所有的插值结果基本上都和原始函数相重合。除了线性插值外，其他插值方法都保持了二阶 TGD 的连续性。

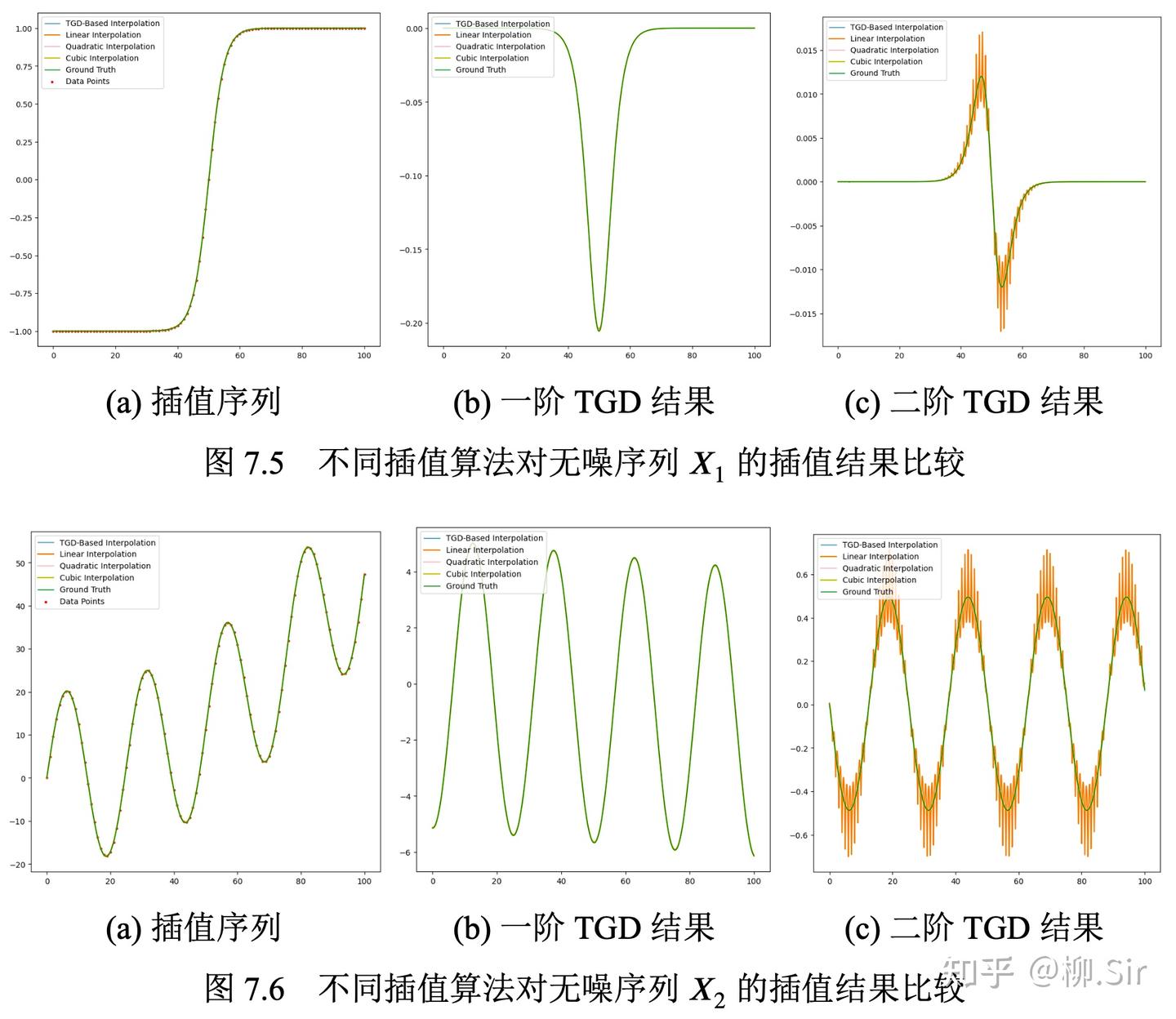
2.3 带噪环境下基于TGD的信号插值

上面对比使用的包括表现最好的三次样条插值等方法高度依赖给定的初始值，并不能够实现对噪声信号的插值。相较而言，基于 TGD 的插值算法则很容易扩展到噪声信号插值任务。假设带噪声环境，从两个平滑函数中分别采样获得两个离散序列，依然需要在每两个给定的点之间插入 $10$ 个新的数据点：

$\begin{array}{l}{X}_1(n)=\tanh \left(\frac{n-50}{5}\right)+\delta (n),n=0,1,\cdots ,100\\ X_2(n)=20\sin \left(\frac{n}{4}\right)+\frac{n^2}{200}+\delta (n),n=0,1,\cdots ,100\end{array}$

其中 $\delta$ 是高斯噪声，对于 $X_1$ 而言是均值为 $0$ 方差为 $0.1$ 的高斯噪声，对于 $X_2$ 而言则是均值为 $0$ 方差为 $2$ 的高斯噪声。实验中基于TGD的插值算法设置和无噪环境下保持一致，唯独损失因子部分，选择 ${\lambda }_{\mathrm{offset}}=0.02$ 、 ${\lambda }_{1\mathrm{st}}=1$ 、 ${\lambda }_{2\mathrm{nd}}=10$ 。

2.3.1 定性分析

带噪序列 $X_1$ 和 $X_2$ 的插值过程如下所示，第一列红色点为带噪声的采样点，第一行展示了初始情况下插值的阶梯函数和对应的TGD值：

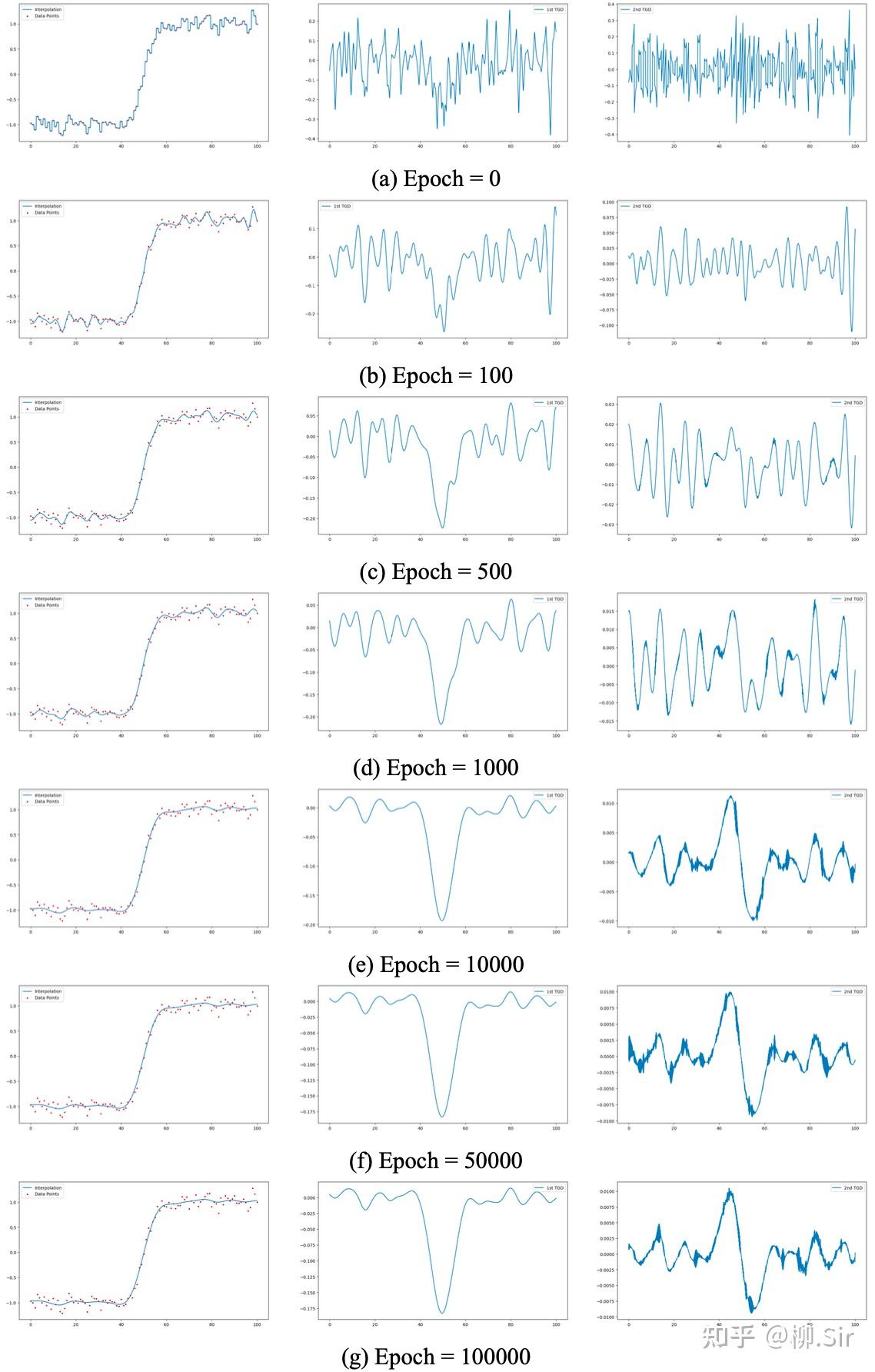
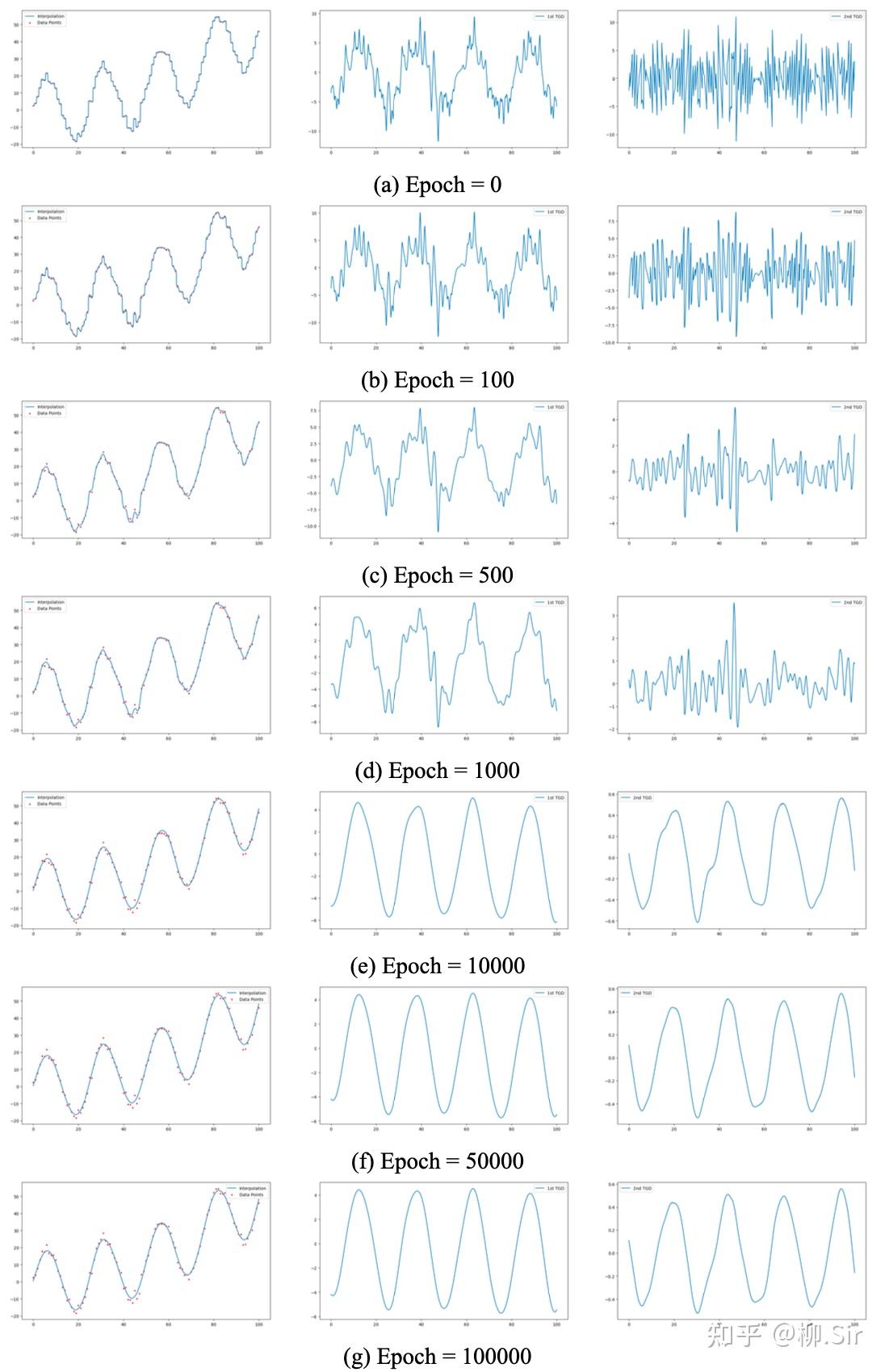
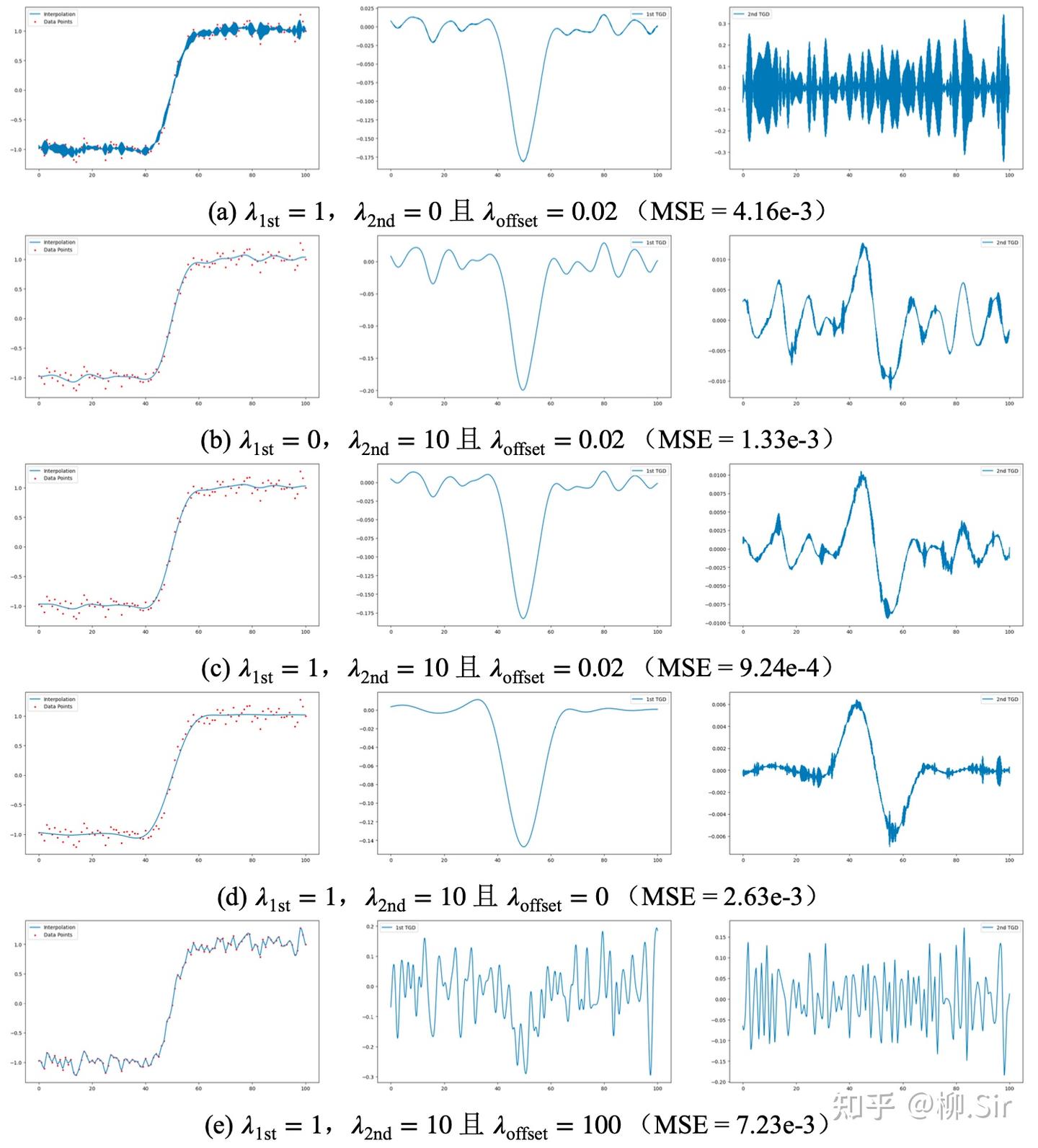
不同损失因子对带噪序列插值结果比较如下所示：第一行展示了当 ${\lambda }_{2\mathrm{nd}}=0$ 时，仅考虑一阶TGD的连续性，也可能损失因子选择不够好，反正性能不佳；第二行展示了当 ${\lambda }_{1\mathrm{st}}=0$ 时，仅考虑二阶TGD的连续性，效果不如第三行同时考虑一阶和二阶连续性。当 ${\lambda }_{\mathrm{offset}}$ 很小或者为 $0$ 时，肯定插值函数更平滑，但是会有信号信息丢失；当 ${\lambda }_{\mathrm{offset}}$ 很大时，去噪效果就不好。 因此，建议在带噪声环境下合理考虑损失函数的所有部分。

2.3.2 定量分析

找了一圈没找到太多可以用于噪声信号插值的算法，我能找到的就是使用 SciPy 插值模块（scipy.interpolate）实现的 UnivariateSpline 一维平滑样条插值方法进行比较，详情请见 SciPy 的文档。

下表定量比较了两大算法，就均方误差而言，基于 TGD 的插值方法优于 UnivariateSpline 插值方法一到两个数量级。但是光看数字还不够，还要看实际插值后的可视化图更直观理解：

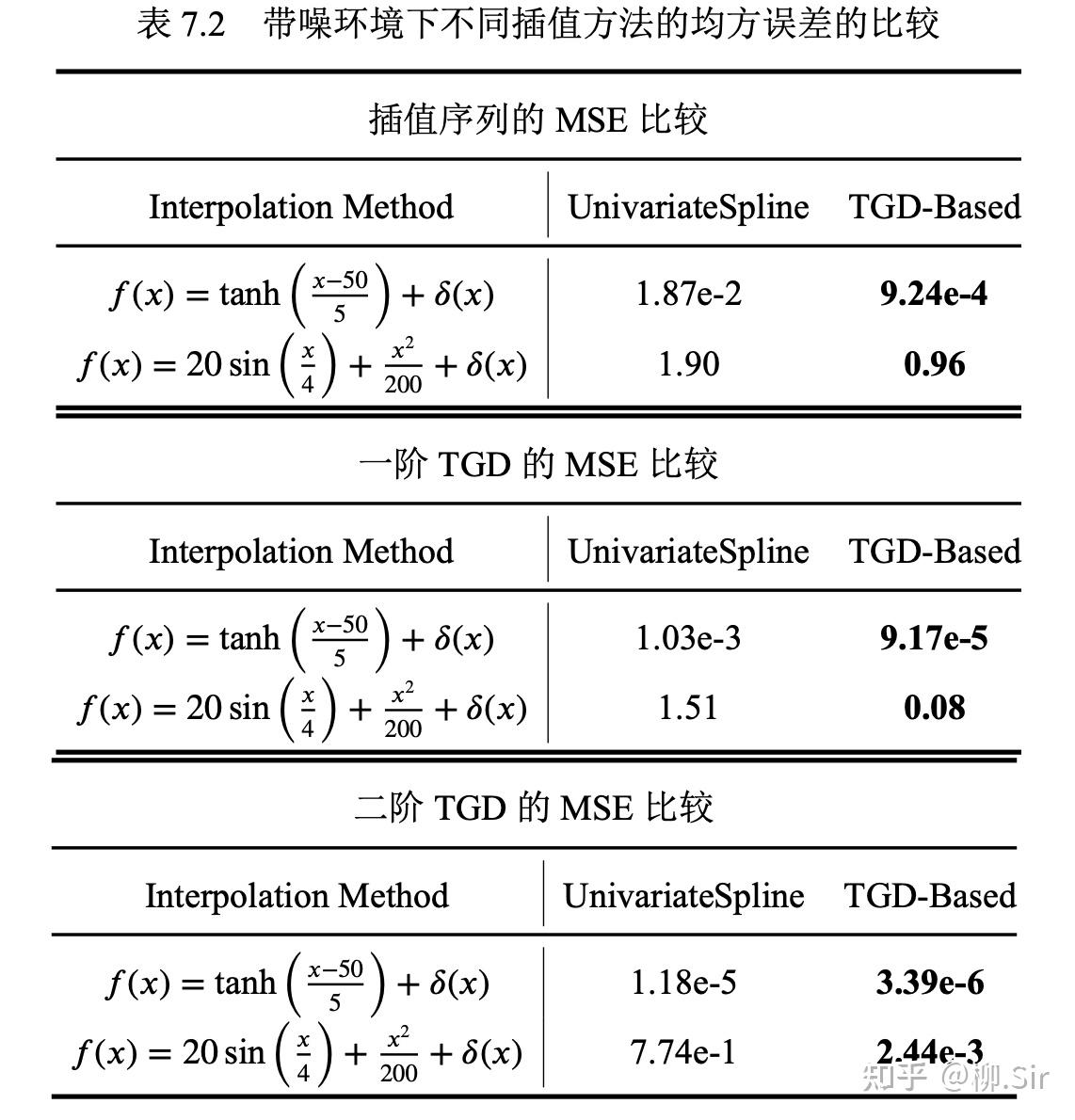
可视化后可见，UnivariateSpline 插值方法实现了插值序列的平滑性，但一阶和二阶的连续性方面可能会丢失，而且插值结果与真实的未知分布差距很大。相比之下，基于 TGD 插值方法在去噪的同时很好地保持了未知初始分布的特性，特别是对信号变化规律的保持。

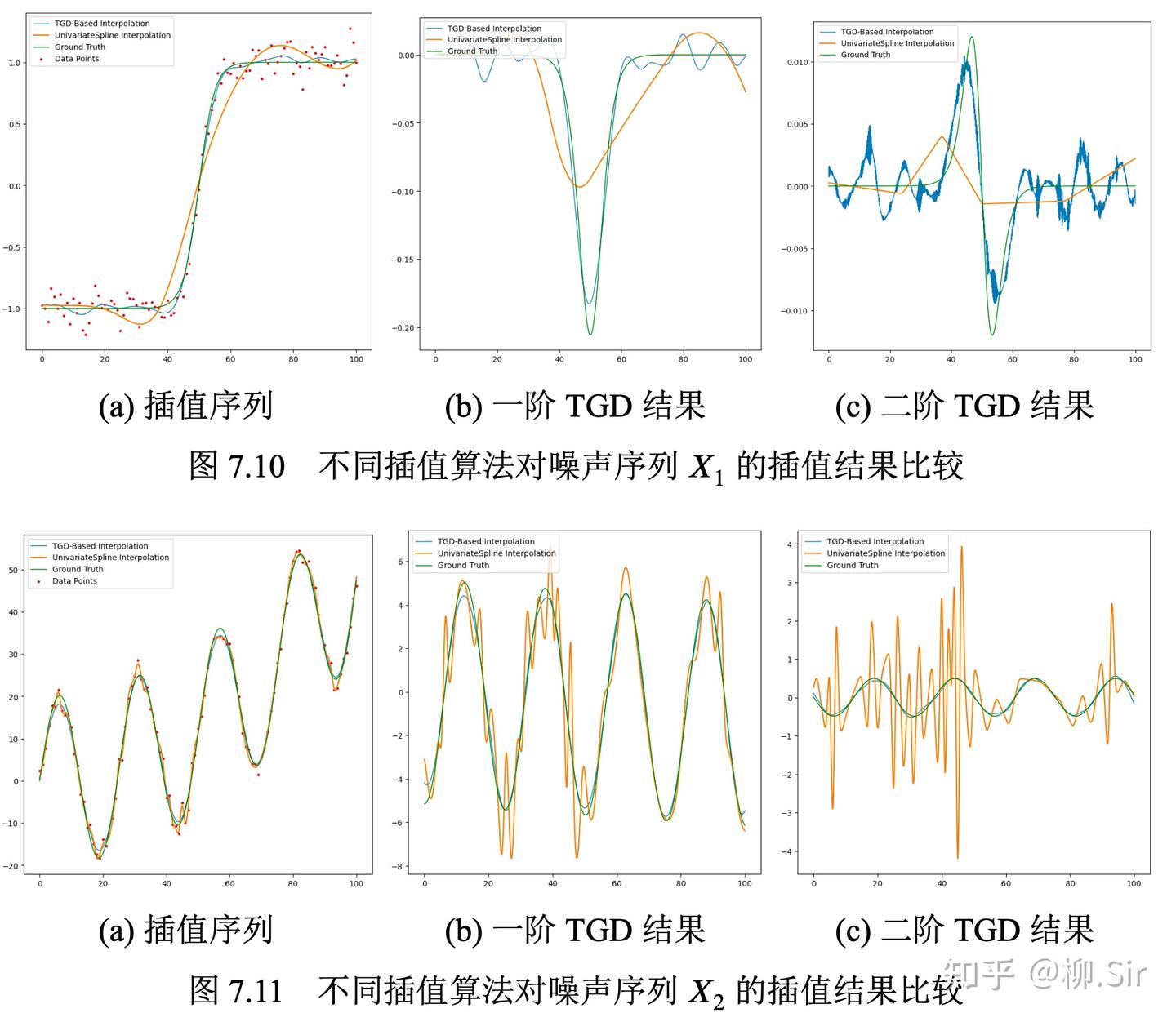
无噪情况下，惜败三次样条插值，但是带噪环境下，吊打样条插值算法。

三、理性交流

有得必有失，有失必有得，葫芦按下去一头肯定要冒起来一头。上面给出的基于TGD的算法实现，是基于梯度反向传递求解非凸优化问题， 最大的问题就是“计算量”和“慢” 。传统的高斯平滑、传统的样条插值，不到0.1秒就能解决的，为什么要用0.3秒、0.5秒来求解呢？

我想说的是，上面的算法不是为了“刷榜”，不是为了SOTA（还记得当年被审稿人问了之后，我和兄弟的王者荣耀ID分别改为了 “您SOTA吗”和“我不SOTA”）。上面的算法是为了验证TGD理论的有效性，是为了展现“一项数学突破可以带来下游算法的革新”，以前做不到的，现在有了新的数学理论和数学工具，可以做了，仅此而已！

四、结语

在一维信号常见任务中的“去噪”和“插值”，乃至“去噪插值”场景下，基于 TGD 的算法展现了不俗的性能。并且它算是一场传统和现代的生动融合，算法是传统的非凸优化算法，实现手段是现在最火热的卷积神经网络。

我不敢说基于TGD的算法是对传统算法的革新，因为思路还是那些思路。但这一定是“ 数学理论突破带来算法自然更新 ”的最佳实践。

TGD理论在一维情况下的实践如此优秀，二维信号处理中强依赖变化率表征的任务，如图像边缘检测，还会差吗？

敬请下回分解，谢谢。

知乎原文地址：TGD第七篇：一维应用——信号去噪和插值