文章目录
1. 数据拟合与最优化方法
1.1. 数据拟合
数据拟合是为了连续化离散的数据,以方便微积分工具在数据上的使用。
例如有数据x代表温度,y代表产量:
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
如图:

怎么去计算温度
x
=
5.5
x=5.5
x=5.5时,产量
y
y
y的大小呢?这就需要用到数据拟合了,通过拟合来将离散的数据点串成连续的函数,就可以计算出函数上任意一点的值。当然拟合的作用不止于此。
下面我们用一组二维数据和一组三维数据来展示MatLab中多种回归拟合模型的使用。
二维数据
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
三维数据
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];

1.1.1. 线性回归 fitlm
https://ww2.mathworks.cn/help/stats/fitlm.html?lang=en
film的输入:
- X,即自变量矩阵;
- Y,即因变量值。
film的输出:
- 回归表达式(Linear regression model),即线性回归表达式;
- 常数项(Intercept),即回归表达式中常数项的值;
- 系数估计值(Estimate),即回归表达式中的系数值;
- 标准误差(Standard Error, SE),即系数的标准误差;
- t统计量(tStat),即每个系数的 t 统计量,tStat = Estimate/SE;
- t 统计量的 p 值(pValue),即假设检验的 t 统计量的 p 值;
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/stats/fitlm.html?lang=en。
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
mdl = fitlm(x1,y);
disp(mdl);
输出:
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ _______ _______
(Intercept) 3.0278 4.3607 0.69434 0.50985
x1 0.68333 0.77491 0.88182 0.40713
表达式为: y = 3.0278 + 0.6833 x 1 y=3.0278+0.6833x_1 y=3.0278+0.6833x1
% 拟合x1、x2与y
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];
mdl = fitlm([x1', x2'],y); % x1'是x1向量转置的意思
disp(mdl);
输出:
Linear regression model:
y ~ 1 + x1 + x2
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ _______ ________
(Intercept) 5.0714 2.7551 1.8407 0.11526
x1 -1.4922 0.7824 -1.9072 0.10512
x2 1.1866 0.33762 3.5147 0.012599
Number of observations: 9, Error degrees of freedom: 6
Root Mean Squared Error: 3.71
R-squared: 0.706, Adjusted R-Squared 0.608
F-statistic vs. constant model: 7.2, p-value = 0.0255
表达式为:
y
=
5.0714
−
1.4922
x
1
+
1.1866
x
2
y=5.0714-1.4922x_1+1.1866x_2
y=5.0714−1.4922x1+1.1866x2

1.1.2. 多项式线性回归 regress
https://ww2.mathworks.cn/help/stats/regress.html?lang=en
regress的输入:
- Y,即因变量值;
- X_matrix,即自变量表达式矩阵,可自定义。
regress的输出:
- 系数估计值(b),即多元线性回归的系数估计值;
- 95% 置信区间(bint),即系数估计值的 95% 置信区间的矩阵;
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/stats/regress.html?lang=en。
```python
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
X = [ones(size(x1')), x1'];
[b, bint] = regress(y', X);
disp(b);
输出:
b=
3.0278
0.6833
表达式为: y = 3.0278 + 0.6833 x 1 y=3.0278+0.6833x_1 y=3.0278+0.6833x1
% 拟合x1、x2与y
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];
X = [ones(size(x1')), x1'.^3, x2']; % 注意这里给自变量x1加上了3次方
[b, bint] = regress(y', X);
disp(b);
输出:
b=
0.9233
-0.0089
1.0100
表达式为:
y
=
0.9233
−
0.0089
x
1
3
+
1.0100
x
2
y=0.9233-0.0089x_1^3+1.0100x_2
y=0.9233−0.0089x13+1.0100x2

1.1.3. 多项式非线性回归 polyfit
https://ww2.mathworks.cn/help/matlab/ref/polyfit.html?lang=en
polyfit的输入:
- X,即自变量值;
- Y,即因变量值;
- n,即多项式次数;
polyfit的输出:
- 系数估计值§,即次数为 n 的多项式 p(x) 的系数;
- 误差估计值(s),s是一个结构体,记录了误差估计值信息;
- 矩 μ \mu μ,分别记录了一阶矩 μ ( 1 ) \mu(1) μ(1)和二阶矩 μ ( 2 ) \mu(2) μ(2);
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/matlab/ref/polyfit.html?lang=en。
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
[p, S, mu] = polyfit(x1, y, 1);
disp(p);
输出:
p=
1.8714 6.4444
表达式为: y = 1.8714 ∗ x 1 + 6.4444 ∗ x 0 y=1.8714*x^1+6.4444*x^0 y=1.8714∗x1+6.4444∗x0
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
[p, S, mu] = polyfit(x2, y, 2); % 这里变成了2
disp(p);
输出:
p=
6.1445 1.8714 0.9827
表达式为:
y
=
6.1445
∗
x
1
2
+
1.8714
∗
x
1
1
+
0.9827
∗
x
1
0
y=6.1445*x_1^2+1.8714*x_1^1+0.9827*x_1^0
y=6.1445∗x12+1.8714∗x11+0.9827∗x10

1.1.4. 自定义非线性回归 fit
https://ww2.mathworks.cn/help/curvefit/fit.html
fit的输入:
- X,即自变量值;
- Y,即因变量值;
- fitType,即拟合函数;
fit的输出:
- 拟合模型(fitobject)
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/curvefit/fit.html。
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
fitobject = fit(x1', y', 'poly2'); % ploy2表示x1的最高项次数为2
disp(fitobject);
输出:
Linear model Poly2:
fitobject(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.8193 (0.4354, 1.203)
p2 = -7.509 (-11.45, -3.573)
p3 = 18.05 (9.476, 26.62)
表达式为: y = 0.8193 ∗ x 1 2 − 7.509 ∗ x 1 1 + 18.05 y=0.8193*x_1^2-7.509*x_1^1+18.05 y=0.8193∗x12−7.509∗x11+18.05
% 拟合x1、x2与y
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];
fitobject = fit([x1', x2'], y', 'poly23'); % ploy23表示x1的最高项次数为2,x2的最高项次数为3
disp(fitobject);
输出:
Linear model Poly23:
fitobject(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
Coefficients:
p00 = -286.4
p10 = 121.3
p01 = 62.76
p20 = -12.85
p11 = -21.57
p02 = -0.4537
p21 = 1.523
p12 = 0.7509
p03 = -0.2724
表达式为: y = − 286.4 + 121.3 ∗ x 1 + 62.76 ∗ x 2 + − 12.85 ∗ x 2 + − 21.57 ∗ x 1 ∗ x 2 + − 0.4537 ∗ x 2 2 + 1.523 ∗ x 1 ∗ x 2 + 0.7509 ∗ x 1 ∗ x 2 2 + − 0.2724 ∗ x 2 3 y=-286.4 + 121.3*x_1 + 62.76*x_2 + -12.85*x^2 + -21.57*x_1*x_2 + -0.4537*x_2^2 + 1.523*x_1*x_2 + 0.7509*x_1*x_2^2 + -0.2724*x_2^3 y=−286.4+121.3∗x1+62.76∗x2+−12.85∗x2+−21.57∗x1∗x2+−0.4537∗x22+1.523∗x1∗x2+0.7509∗x1∗x22+−0.2724∗x23

1.1.5. 自定义非线性最小二乘法回归 lsqcurvefit
https://ww2.mathworks.cn/help/optim/ug/lsqcurvefit.html
lsqcurvefit的输入:
- fun,即拟合函数;
- x0,即初始化X值。
- X,即自变量值;
- Y,即因变量值;
- lb,自变量的下限
- ub,自变量的上限
lsqcurvefit的输出:
- 自变量系数(x)
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/optim/ug/lsqcurvefit.html。
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
beta0 = [1 1 1];
fun = @(beta0, x1)( beta0(1).*x1.^2 + beta0(2).*x1 + beta0(3));
lb = [0];
ub = [10];
x_result = lsqcurvefit(fun, beta0, x1, y, lb, ub);
disp(x_result);
输出:
x=
0.8193 -7.5093 18.0476
表达式为: y = 0.8193 ∗ x 1 2 − 7.509 ∗ x 1 1 + 18.0476 y=0.8193*x_1^2-7.509*x_1^1+18.0476 y=0.8193∗x12−7.509∗x11+18.0476
% 拟合x1、x2与y
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];
beta0 = [1 1 1];
X = [x1' x2'];
fun = @(beta0, X)( beta0(1).*X(:,1).^2 + beta0(2).*X(:,2).^2 + beta0(3));
lb = [0, -2];
ub = [10, 20];
x_result = lsqcurvefit(fun, beta0, X, y', lb, ub);
disp(x_result);
输出:
x=
0.0000 0.0370 3.0720
表达式为: y = 0.0000 ∗ x 1 2 − 0.0370 ∗ x 2 2 + 3.0720 y=0.0000*x_1^2-0.0370 *x_2^2+3.0720 y=0.0000∗x12−0.0370∗x22+3.0720

1.1.6. 自定义非线性牛顿法回归 nlinfit
https://ww2.mathworks.cn/help/stats/nlinfit.html?lang=en
nlinfit的输入:
- X,即自变量值;
- Y,即因变量值;
- model,即拟合函数;
- beta0,即初始化X值。
nlinfit的输出:
- 自变量系数(beta)
- 其余参数查看matlab官网 https://ww2.mathworks.cn/help/stats/nlinfit.html?lang=en。
% 拟合x1与y
x1 = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
beta0 = [1 1 1];
fun = @(beta0, x1)( beta0(1).*x1.^2 + beta0(2).*x1 + beta0(3));
beta = nlinfit(x1, y, fun, beta0);
disp(beta);
输出:
beta=
0.8193 -7.5093 18.0476
表达式为: y = 0.8193 ∗ x 1 2 − 7.509 ∗ x 1 1 + 18.0476 y=0.8193*x_1^2-7.509*x_1^1+18.0476 y=0.8193∗x12−7.509∗x11+18.0476
% 拟合x1、x2与y
x1 = [1 2 3 4 5 6 7 8 9];
x2 = [5 4 3 2 0 9 10 15 19];
y = [9 7 6 3 -1 2 5 7 20];
beta0 = [1 1 1];
X = [x1' x2'];
fun = @(beta0, X)( beta0(1).*X(:,1).^2 + beta0(2).*X(:,2).^2 + beta0(3));
beta = nlinfit(X, y', fun, beta0);
disp(beta);
输出:
beta=
-0.2973 0.0988 6.8492
表达式为: y = − 0.2973 ∗ x 1 2 − 0.0988 ∗ x 2 2 + 6.8492 y=-0.2973*x_1^2-0.0988*x_2^2+6.8492 y=−0.2973∗x12−0.0988∗x22+6.8492

1.1.7. 拟合工具箱 Curve Fitting
Curve Fitting是Matlab中一个方便快捷的函数拟合工具箱,优点就是方便,直观,可以自动出图,而且图像还可以任意角度旋转查看,但是无法拟合高于3维的数据。

1.2. 最优化方法
在有了函数表达式之后,如何求最优值通常是一个巨大的挑战,所以学习一些最优化知识是必要的。
1.2.1. 无约束优化问题
所谓无约束优化问题,就是指对一个函数求最优值,最优值可以出现在函数上任意一点,而不去限定查找最优值的范围。
无约束优化问题通常有四种优化方法:
- Newton’s method(牛顿法);
- Levenberg-Marquardt’s method(LM);
- Broyden-Fletcher-Goldfarb-Shanno’s method(BFGS);
- Davidon-Fletcher-Powell’s method(DFP)
假设有如下无约束优化问题:
f
(
x
1
,
x
2
)
=
(
x
1
−
3
)
4
+
(
x
1
−
3
x
2
)
2
f(x_1,x_2)=(x_1-3)^4+(x_1-3x_2)^2
f(x1,x2)=(x1−3)4+(x1−3x2)2

下面我们来用matlab实现一下这四种优化算法:
无约束优化问题中牛顿法与拟牛顿法四种迭代方法的matlab实现
1.2.2. 约束优化问题
约束优化问题就是指给自变量 x x x的取值范围做限制,缩小优化范围,经典的约束优化算法有:
- 内点法(interior-point)
- 有效集法(active-set)
- SQP算法(sqp)
- 信赖域反射法(trust-region-reflective)
约束,又分线性约束与非线性约束,所谓线性约束,就是指约束条件中的自变量都是1次幂的,非线性约束即有高次幂的自变量。
假设有如下约束优化函数和约束:
min
f
(
x
1
,
x
2
)
=
−
x
1
x
2
\min f(x_1,x_2)=-x_1x_2
minf(x1,x2)=−x1x2
s
.
t
.
1
−
x
1
2
−
x
2
2
⩾
0
s.t.\quad 1-x_1^2-x_2^2\geqslant 0
s.t.1−x12−x22⩾0

那么优化器方法可以定义为:
function [xsol, fval] = runfmincon
% 初始点
x0 = [-0.1 -0.1];
% 四种优化算法,选一种用,这里用的是内点法
% 'active-set', 'interior-point', 'sqp', or 'trust-region-reflective'.
options = optimset('Display', 'iter-detailed', 'Algorithm', 'interior-point', 'MaxIter', 8); % 优化器参数
% fmincon参数解释
% fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
% fun:要优化的函数
% x0:自变量的初始值
% A:非等式(<)线性约束的约束矩阵A
% b:非等式(<)线性约束的约束条件矩阵b
% Aeq:等式约束的线性约束的约束矩阵Aeq
% beq:等式线性约束的约束条件矩阵beq
% lb,ub:自变量的下限和上限
% nonlcon:非线性约束
[xsol, fval] = fmincon(@objfun, x0, [], [], [], [], [], [], @confun, options);
% 目标函数
function f = objfun(x)
f = - x(1) * x(2);
end
% 非线性约束
function [c, ceq] = confun(x)
% Nonlinear inequality constraints
c = [x(1)^2 + x(2)^2 - 1];
% Nonlinear equality constraints
ceq = [];
end
end
优化结果:
[xsol,fval] = runfmincon;
% 迭代优化结果1
[x1,x2]=[-0.7071,-0.7071]
f=-0.5
% 迭代优化结果2
[x1,x2]=[0.7071,0.7071]
f=-0.5

2. 神经网络与特征选择
2.1. 神经网络
神经网络有两种功能,一是分类,二是回归,下面分别是两种神经网络的python代码。通常会使用pytorch框架来实现神经网络,可以参考博客:从细节过渡到实例 一天学会Pytorch
2.1.1. 分类神经网络
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
# 构造数据
n_data = torch.ones(100, 2)
x0 = torch.normal(3*n_data, 1)
x1 = torch.normal(-3*n_data, 1)
# 标记为y0=0,y1=1两类标签
y0 = torch.zeros(100)
y1 = torch.ones(100)
# 通过.cat连接数据
x = torch.cat((x0, x1), 0).type(torch.float)
y = torch.cat((y0, y1), 0).type(torch.long)
# 构造一个简单的神经网络
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.inLayer = torch.nn.Linear(n_feature, n_hidden) # 输入层
self.hiddenLayer = torch.nn.Linear(n_hidden, n_hidden) # 隐藏层
self.outLayer = torch.nn.Linear(n_hidden, n_output) # 输出层
# 前向计算函数,定义完成后会隐式地自动生成反向传播函数
def forward(self, x):
x = F.relu(self.hiddenLayer(self.inLayer(x)))
x = self.outLayer(x)
return x
net = Net(2, 10, 2) # 初始化一个网络,2个输入层节点,10个隐藏层节点,2个输出层节点
loss_func = torch.nn.CrossEntropyLoss() # 定义交叉熵损失函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 配置网络优化器
# 将网络模型、损失函数和输入张量迁入GPU
if(torch.cuda.is_available()):
net = net.cuda()
loss_func = loss_func.cuda()
x, y = x.cuda(), y.cuda()
# 训练模型
out = net(x)
for t in range(300):
out = net(x) # 将数据输入网络,得到输出
loss = loss_func(out, y) # 得到损失
optimizer.zero_grad() # 梯度初始化
loss.backward() # 反向传播
optimizer.step() # 对网络进行优化
# 使用模型进行预测
prediction = torch.max(F.softmax(out, dim=0), 1)[1]
pred_y = prediction.data.cpu().numpy().squeeze()
# 可视化
plt.scatter(x.data.cpu().numpy()[:, 0], x.data.cpu().numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlBu')
plt.show()

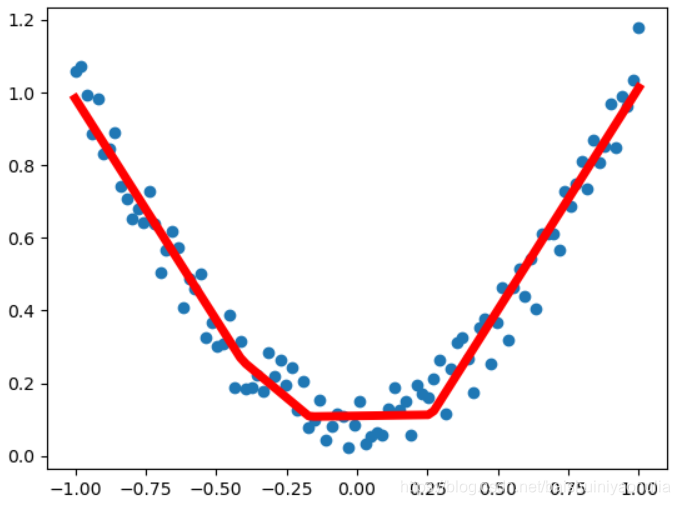
2.1.2. 回归神经网络
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
# 构造数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2 * torch.rand(x.size())
# 构造一个简单的神经网络
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.inLayer = torch.nn.Linear(n_feature, n_hidden) # 输入层
self.hiddenLayer = torch.nn.Linear(n_hidden, n_hidden) # 隐藏层
self.outLayer = torch.nn.Linear(n_hidden, n_output) # 输出层
# 前向计算函数,定义完成后会隐式地自动生成反向传播函数
def forward(self, x):
x = F.relu(self.hiddenLayer(self.inLayer(x)))
x = self.outLayer(x)
return x
net = Net(1, 10, 1) # 初始化一个网络,1个输入层节点,10个隐藏层节点,1个输出层节点
loss_func = torch.nn.MSELoss() # 定义均方误差损失函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 配置网络优化器
# 将网络模型、损失函数和输入张量迁入GPU
if(torch.cuda.is_available()):
net = net.cuda()
loss_func = loss_func.cuda()
x, y = x.cuda(), y.cuda()
# 训练模型
out = net(x)
for t in range(300):
out = net(x) # 将数据输入网络,得到输出
loss = loss_func(out, y) # 得到损失
optimizer.zero_grad() # 梯度初始化
loss.backward() # 反向传播
optimizer.step() # 对网络进行优化
# 可视化
plt.scatter(x.data.cpu().numpy(), y.data.cpu().numpy())
plt.plot(x.data.cpu().numpy(), out.data.cpu().numpy(), 'r-', lw=5)
plt.show()
2.2. 特征选择
尽管神经网络是一个优秀的分类回归器,但是也不意为着它是万能的,在神经网络拟合的效果不好的情况下,还需要先进行特征筛选,也就是选出最适合的特征,再将它们输入神经网络进行训练。一个优秀的特征选择器是决策树,或者随机森林。
scikit-learn:决策树
scikit-learn:随机森林
在决策树中,有几个重要的概念就是“信息熵、条件熵、信息增益及信息增益比”
- 信息熵
信息熵表示了信息的不确定性,也就是一个特征对结果影响的不确定性; - 条件熵
条件熵指的是在其他特征作用的情况下,某特征对结果影响的不确定性。 - 信息增益
信息增益 = 信息熵 - 条件熵。信息增益指的是在其他特征作用的情况下,某特征对结果的不确定性的减小程度。 - 信息增益比
信息增益比是一种对信息增益的归一化。
信息熵、条件熵、信息增益及信息增益比的应用举例
决策树中熵、条件熵、信息增益及信息增益比的python实现

























 929
929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










