leetcode085_221：Maximal Rectangle&Maximal Square

题目描述

• Maximal Rectangle:
  Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing all ones and return its area.
• Maximal Square
  Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing all 1’s and return its area.

问题分析

要求01矩阵中由1组成的最大矩阵的面积。这类题目可以通过记录每个点的向左延伸长度和向上延伸高度来求出每个点作为矩阵右下顶点时的最大矩阵面积。显然对于点为0的点面积为0.所以只对点为1的点进行考虑。现在问题就变为怎么求以该点为矩阵右下顶点时的最大矩阵面积，而对于Maximal Square即求以该点为矩阵右下顶点时的最大正方形面积。
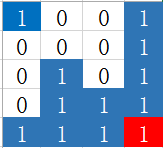
在给定每个点的向上高度如何求最大边长呢？看图：

红色代表将要求最大面积的点。对于Maximal Rectangle，从右往左尝试，每次记录下当前能组成最大矩阵时的高度值的索引，遍历结束时可以找到答案；对于Maximal Square，从左往右，初始边长为该红点向左的最长宽度，如果发现高度小于边长，需要更新当前边长，否则保持不变，最后得到的边长平方就是答案。
附代码：

//Maximal Rectangle:20ms
int wid[1000][1000];
int hei[1000][1000];
int area1[1000][1000];
class Solution {
public:
    int maxArea(int l,int r, int row) {
        int ans = 0;
        int cur = r;
        for (int k = r; k >= l+1; k--)  {
            if (hei[row][k - 1] >= hei[row][cur]) continue;
            else {
                ans = max(ans, hei[row][cur]*(r - k + 1));
                cur = k - 1;
            }
        }
        ans = max(ans, hei[row][cur] * (r - l + 1));
        return ans;
    }
    int maximalRectangle(vector<vector<char>>& matrix) {
        int ans = 0;
        int m = matrix.size();
        if (!m) return ans;
        int n = matrix[0].size();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '0') {
                    wid[i][j] = hei[i][j] = 0;
                }
                else {
                    int area = 0;
                    if (!i&&!j) {
                        wid[i][j] = hei[i][j] = 1;
                        area = 1;
                    }
                    else if (!i) {
                        wid[i][j] = wid[i][j - 1] + 1;
                        hei[i][j] = 1;
                        area = wid[i][j];
                    }
                    else if(!j) {
                        wid[i][j] = 1;
                        hei[i][j] = hei[i - 1][j] + 1;
                        area = hei[i][j];
                    }
                    else {
                        wid[i][j] = 1 + wid[i][j - 1];
                        hei[i][j] = 1 + hei[i - 1][j];
                        area = max(area, maxArea(j - wid[i][j] + 1, j, i));
                    }
                    ans = max(area, ans);
                    area1[i][j] = area;
                }
            }
        }
        return ans;
    }
};
//Maximal Square:16ms
int wid[1000][1000];
int hei[1000][1000];
int area1[1000][1000];
class Solution {
public:
    int maxArea(int l, int r, int row) {
        int side = r - l + 1;
        for (int i = l; i <= r; i++) {
            if (hei[row][i] >= side) {
                continue;
            }
            else {
                side = r - i;
            }
        }
        return side*side;
    }
    int maximalSquare(vector<vector<char>>& matrix) {
        int ans = 0;
        int m = matrix.size();
        if (!m) return ans;
        int n = matrix[0].size();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '0') {
                    wid[i][j] = hei[i][j] = 0;
                }
                else {
                    int area = 0;
                    if (!i&&!j) {
                        wid[i][j] = hei[i][j] = 1;
                        area = 1;
                    }
                    else if (!i) {
                        wid[i][j] = wid[i][j - 1] + 1;
                        hei[i][j] = 1;
                        area = 1;
                    }
                    else if (!j) {
                        wid[i][j] = 1;
                        hei[i][j] = hei[i - 1][j] + 1;
                        area = 1;
                    }
                    else {
                        wid[i][j] = 1 + wid[i][j - 1];
                        hei[i][j] = 1 + hei[i - 1][j];
                        area = max(area, maxArea(j - wid[i][j] + 1, j, i));
                    }
                    ans = max(area, ans);
                    area1[i][j] = area;
                }
            }
        }
        return ans;
    }
};