最优化理论公式大赏（下）

动态规划

连续函数

• 用动态规划法的顺序法求解下列问题：
  $$\begin{gathered} \max z=x_1{x}_2^2{x}_3 \\ s.t.\{\begin{array}{c}{x}_1+2x_2+4x_3=8\\ x_i\ge 0,i=1,2,3\end{array} \end{gathered}$$
• 为了便于分析，作换元$y_1=x_1,y_2=2x_2,y_3=4x_3$，将原命题变成：
  $$\begin{gathered} \max z=\frac{1}{16}{y}_1{y}_2^2{y}_3 \\ s.t.\{\begin{array}{c}{y}_1+y_2+y_3=8\\ y_i\ge 0,i=1,2,3\end{array} \end{gathered}$$
• 该命题的现实意义为“假设有8百万资金可以投给三家工厂，求它们的某种总效益的最大值”。
• （1）假设总资金为u₁，为工厂1投资y₁，总效益为$\frac{1}{16}{y}_1$，其最大值为z₁(u₁)。
  显然，当y₁=u₁时，$z_1(u_1)=\underset{0\le y_1\le u_1}{\max }(\frac{1}{16}{y}_1)=\frac{1}{16}{u}_1$。
• （2）假设总资金为u₂，为工厂2投资y₂，将剩余资金(u₂-y₂)投给工厂1，总效益为$\frac{1}{16}{y}_1{y}_2^2$，其最大值为：
  $$\begin{gathered} z_2(u_2) \\ =\underset{0\le y_2\le u_2}{\max }(y_2^2{z}_1(u_2-y_2)) \\ =\underset{0\le y_2\le u_2}{\max }(\frac{1}{16}{y}_2^2(u_2-y_2)) \\ =\frac{1}{16}{y}_2^2(u_2-y_2){|}_{2u_2{y}_2-3y_2^2=0} \\ =\frac{1}{16}{y}_2^2(u_2-y_2){|}_{y_2=\frac{2}{3}{u}_2} \\ =\frac{1}{108}{u}_2^3,y_2=\frac{2}{3}{u}_2 \end{gathered}$$
• （3）假设总资金为u₃，为工厂3投资y₃，将剩余资金(u₃-y₃)投给工厂1和2，总效益为$\frac{1}{16}{y}_1{y}_2^2{y}_3$，其最大值为：
  $$\begin{gathered} z_3(u_3) \\ =\underset{0\le y_3\le u_3}{\max }(y_3{z}_2(u_3-y_3)) \\ =\underset{0\le y_3\le u_3}{\max }(\frac{1}{108}{y}_3(u_3-y_3{)}^3) \\ =\frac{1}{108}{y}_3(u_3-y_3{)}^3){|}_{(u_3-y_3{)}^3-3y_3(u_3-y_3{)}^2=0} \\ =\frac{1}{108}{y}_3(u_3-y_3{)}^3){|}_{y_3=\frac{1}{4}{u}_3} \\ =\frac{1}{1024}{u}_3^4,y_3=\frac{1}{4}{u}_3 \end{gathered}$$
• 题目中只有三个阶段，且总资金为8百万。因此，$u_3=8,z_{\max }=z_3(8)=\frac{8^4}{1024}=4$。
  相应地，$y_3=2,u_2=8-2=6,y_2=\frac{2}{3}{u}_2=4,y_1=u_1=u_2-y_2=2$。
  综上所述，当$x_1=y_1=2,x_2=\frac{1}{2}{y}_2=2,x_3=\frac{1}{4}{y}_3=\frac{1}{2}$时，z取得最小值4。
• 考试时建议用拉格朗日乘数法求一遍准确解以供验算。如果你实在整不来动态规划，也可以借助拉格朗日乘数法在依托答辩般的计算过程末尾强行搞出一个正确的答案。
• 逆序法只不过是把求解顺序改变了，即从y₃向y₁分析。最先被分析的阶段虽然叫第三阶段，但总效益写作z₁。

离散函数

• 离散函数的动态规划中，最典的是用于求两地之间的最短路程。老师说，有了算力无穷的，超越维度的民用量子计算机之后，就再也不用管什么算法了，硬枚举就完事了，但你毕业之前肯定遇不到。
• 假设有A、B、C、D、E五座城市，它们之间的路程为$\left[\begin{array}{cccccc}& A& B& C& D& E\\ A& 0& 6& 5& 2& 2\\ B& 6& 0& 0.5& 5& 7\\ C& 5& 0.5& 0& 1& 5\\ D& 2& 5& 1& 0& 3\\ E& 2& 7& 5& 3& 0\end{array}\right]$。求E城到其它四座城市之间的最短路程。

函数空间迭代法：

• 设f_n(X)代表所走路程的段数不超过n时从X城到E城的最短路程，n=1,2,3,4。
• n=1时，显然$\begin{array}{c}{f}_1(A)=2\\ f_1(B)=7\\ f_1(C)=5\\ f_1(D)=3\end{array}$
• n=2时，$\begin{array}{c}{f}_2(A)=\min [f_1(A),6+f_1(B),5+f_1(C),2+f_1(D)]=2\\ f_2(B)=\min [6+f_1(A),f_1(B),0.5+f_1(C),5+f_1(D)]=5.5\\ f_2(C)=\min [5+f_1(A),0.5+f_1(B),f_1(C),1+f_1(D)]=4\\ f_2(D)=\min [2+f_1(A),5+f_1(B),1+f_1(C),f_1(D)]=3\end{array}$
• n=3时，$\begin{array}{c}{f}_3(A)=\min [f_2(A),6+f_2(B),5+f_2(C),2+f_2(D)]=2\\ f_3(B)=\min [6+f_2(A),f_2(B),0.5+f_2(C),5+f_2(D)]=4.5\\ f_3(C)=\min [5+f_2(A),0.5+f_2(B),f_2(C),1+f_2(D)]=4\\ f_3(D)=\min [2+f_2(A),5+f_2(B),1+f_2(C),f_2(D)]=3\end{array}$
• n=4时，$\begin{array}{c}{f}_4(A)=\min [f_3(A),6+f_3(B),5+f_3(C),2+f_3(D)]=2\\ f_4(B)=\min [6+f_3(A),f_3(B),0.5+f_3(C),5+f_3(D)]=4.5\\ f_4(C)=\min [5+f_3(A),0.5+f_3(B),f_3(C),1+f_3(D)]=4\\ f_4(D)=\min [2+f_3(A),5+f_3(B),1+f_3(C),f_3(D)]=3\end{array}$
• 因此，从A到E的最短路径为A-E，路程为2；从B到E的最短路径为B-C-D-E，路程为4.5；从C到E的最短路径为C-D-E，路程为4；从D到E的最短路径为D-E，路程为3。
• 用顺序法求一个网络的最优路径时，设f(X)为从起点到X点的最优路径，从起点往终点推理，反之亦然。

策略空间迭代法：

• 任选一个没有回路的初始策略，如$u_0(A)=u_0(B)=u_0(C)=u_0(D)=E$，u_i(X)=Y代表第i次迭代时将X的下一步作为Y是目前从X走到E的最优走法。同时，f_n(X)也会被顺便解出来。
• 解方程组$\{\begin{array}{c}{f}_0(A)=|AE|+f_0(E)=2\\ f_0(B)=|BE|+f_0(E)=7\\ f_0(C)=|CE|+f_0(E)=5\\ f_0(D)=|DE|+f_0(E)=3\end{array}$，得$\{\begin{array}{c}{f}_0(A)=2\\ f_0(B)=7\\ f_0(C)=5\\ f_0(D)=3\end{array}$
• 由$\{\begin{array}{c}\min [f_0(A),|AB|+f_0(B),|AC|+f_0(C),|AD|+f_0(D)]=f_0(A)\\ \min [|BA|+f_0(A),f_0(B),|BC|+f_0(C),|BD|+f_0(D)]=|BC|+f_0(C)\\ \min [|CA|+f_0(A),|CB|+f_0(B),f_0(C),|CD|+f_0(D)]=|CD|+f_0(D)\\ \min [|DA|+f_0(A),|DB|+f_0(B),|DC|+f_0(C),f_0(D)]=f_0(D)\end{array}$得$\{\begin{array}{c}{u}_1(A)=E\\ u_1(B)=C\\ u_1(C)=D\\ u_1(D)=E\end{array}$
• 解方程组$\{\begin{array}{c}{f}_1(A)=|AE|+f_1(E)\\ f_1(B)=|BC|+f_1(C)\\ f_1(C)=|CD|+f_1(D)\\ f_1(D)=|DE|+f_1(E)\end{array}$，得$\{\begin{array}{c}{f}_1(A)=2\\ f_1(B)=4.5\\ f_1(C)=4\\ f_1(D)=3\end{array}$
• 由$\{\begin{array}{c}\min [f_1(A),|AB|+f_1(B),|AC|+f_1(C),|AD|+f_1(D)]=f_1(A)\\ \min [|BA|+f_1(A),f_1(B),|BC|+f_1(C),|BD|+f_1(D)]=|BC|+f_1(C)\\ \min [|CA|+f_1(A),|CB|+f_1(B),f_1(C),|CD|+f_1(D)]=|CD|+f_1(D)\\ \min [|DA|+f_1(A),|DB|+f_1(B),|DC|+f_1(C),f_1(D)]=f_1(D)\end{array}$得$\{\begin{array}{c}{u}_2(A)=E\\ u_2(B)=C\\ u_2(C)=D\\ u_2(D)=E\end{array}$，与前一步的结果相同。因此可得到最优解f([A,B,C,D])=[2,4.5,4,3]。

Hopfield网络

• Hopfield网络里有n个形成全连接的神经元，其中第i个神经元和第j个神经元之间的权重为w_ij，它们组成n阶权重矩阵W，W为对称方阵且对角线元素都为0。该网络还有一个输入向量v和n维阈值向量θ。
• 在第t步，网络的能量函数为$E(t)=-\frac{1}{2}{\vec{v}}_t^{T}W{\vec{v}}_t+{\vec{\theta }}^T{\vec{v}}_t$，能量总是变得越来越小，即$E(t+1)\le E(t)$。能量达到最小值时，即为求得最优解/最优模式。
• 每步随机选取一个神经元i，选用sgn(x)为非线性激活函数，则有$v_i^{(t+1)}=\mathrm{sgn}({\vec{w}}_{ri}{\vec{v}}_t-{\theta }_i)$，${\vec{w}}_{ri}$代表权重矩阵W的第i行。若状态不变，即${\vec{v}}_{t+1}={\vec{v}}_t$，则计算终止。

联想记忆

• Hopfield网络可以用于对稳定模式进行联想记忆，即“输入像哪个稳定模式，网络就向它收敛”。
• 在稳定模式已知时，使用Hebb学习规则求权重：若给定m个稳定模式$x_1,x_2,\cdots ,x_m$让Hopfield网络记忆（在优化问题中代表m个极小值），则根据Hebb学习规则可得该网络的权重矩阵$W={\sum }_{i=1}^{m}f({\vec{x}}_i{\vec{x}}_i^T)$，f(A)表示将A的对角线元素清零。

求最优解

• Hopfield网络可以用于求最优化问题，如旅行商问题和二分图问题。以二分图问题为例，如下图所示的电路板上有10个元件和若干导线，现需要用一条曲线将电路板分成两部分，要求两部分电路中的元件数量相同，且曲线穿过的导线数尽量少。
  
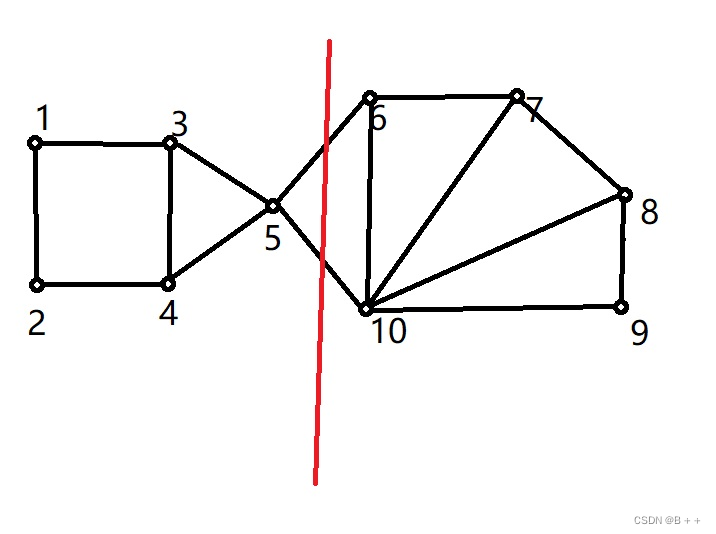
• 上述元件的导线连接方式可用连接性矩阵$W=\left[\begin{array}{cccccccccc}0& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 1& 1& 0& 1& 0& 0& 0& 1\\ 0& 0& 0& 0& 1& 0& 1& 0& 0& 1\\ 0& 0& 0& 0& 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 0& 1& 1& 1& 1& 1& 0\end{array}\right]$表示，w_ij=1（0）代表第i和第j个元件之间（没）有导线相连。同时，板被分割后元件的状态可用10维向量$\vec{v}$表示，v_i∈{-1,1}，具有相同v值的元件在同一块板上。
• 于是，该问题的数学模型可表示为：
  max ⁡ ∑ ∑ v i v j w i j = v ⃗ T W v ⃗ s . t . { ∑ v i = 0 v i ∈ { − 1 , 1 } , i = 1 , 2 , 3 , ⋯ , n \max ∑∑v_iv_jw_{ij}=\vec v^TW\vec v\\s.t.\left\{\begin{matrix}∑v_i=0\\v_i∈\{-1,1\},i=1,2,3,⋯,n\end{matrix}\right. max∑∑vi​vj​wij​=v TWv s.t.{∑vi​=0vi​∈{−1,1},i=1,2,3,⋯,n​
• 用拉格朗日乘数法可将原问题转换为使能量函数$E=-\frac{1}{2}{\vec{v}}^{T}W\vec{v}+\frac{\lambda }{2}(\sum v_i{)}^2$最小化。
• 任取一个满足$\sum v_i=0$的初始状态${\vec{v}}_0$和拉格朗日常数λ，在第m轮，计算第i=(m+10)%10个神经元：$v_i^{(t+1)}=\mathrm{sgn}({\sum }_{j=1}^n(w_{ij}-\lambda )v_j)=\mathrm{sgn}({\vec{w}}_{ri}{\vec{v}}_t-\lambda \sum v_i^{(t)})$。若v_i变号，为了满足约束条件，还要随机选一个与v_i异号的神经元与之同时变号。

模拟退火算法

• 以背包问题为例：假设有n件物品，它们的质量为向量$\vec{m}$，价值为向量$\vec{p}$，背包可容纳的最大物品质量为M；向量$\vec{x}$为n件物品的状态，x_i=1（0）代表（不）拿第i件物品；模拟退火温度为T。
• 背包问题的数学模型为：
  max ⁡ p ⃗ T x ⃗ s . t . { w ⃗ T x ⃗ ≤ M x i ∈ { 0 , 1 } , i = 1 , 2 , 3 , ⋯ , n \max \vec p^T\vec x\\s.t.\left\{\begin{matrix}\vec w^T\vec x≤M\\x_i∈\{0,1\},i=1,2,3,⋯,n\end{matrix}\right. maxp ​Tx s.t.{w Tx ≤Mxi​∈{0,1},i=1,2,3,⋯,n​
• 设E为代价函数（或能量），λ为拉格朗日乘子，则上述模型可变为：
  $\min -{\vec{p}}^T\vec{x}+\max [0,\lambda ({\vec{w}}^T\vec{x}-M)]$
  其意义是使物品的总价值最大化，但背包超重时则需要罚款，超重越多则罚款也越多。
• 在每步迭代中，随机将一样物品放入或拿出背包，即随机改变一个x值。然后计算状态转移概率$P_k=\exp (\frac{E_{k-1}-E_k}{T})$，再从0~1之间取一个均匀分布的随机数。若该随机数小于（大于）P_k，则接受（拒绝）该改变。
• 可见，如果总能量变小则必然接受新的改变，否则要“看AI的心情”决定是否改变。爱因斯坦说上帝不掷骰子，但妹说AI不能掷。