【转】git生成diff原理：Myers差分算法

已于 2022-08-11 13:46:47 修改
阅读量2.1k 收藏 16
点赞数 6
分类专栏： 其他 文章标签： 算法
于 2022-08-11 13:39:38 首次发布
原文链接：https://chenshinan.github.io/2019/05/02/git%E7%94%9F%E6%88%90diff%E5%8E%9F%E7%90%86%EF%BC%9AMyers%E5%B7%AE%E5%88%86%E7%AE%97%E6%B3%95/
版权

转载：git生成diff原理：Myers差分算法 | 大艺术家_SN

什么是Myers差分算法

举一个最常见的例子，我们使用git进行提交时，通常会使用git diff --cached来查看这次提交做了哪些改动，这里我们先简单定义一下什么是diff：diff就是目标文本和源文本之间的区别，也就是将源文本变成目标文本所需要的操作。Myers算法由Eugene W.Myers在1986年发表的一篇论文中提出，是一个能在大部分情况产生”最短的直观的“diff的一个算法。

diff与图搜索

”寻找最短的直观的diff”是一个非常模糊的问题，首先，我们需要把这个问题抽象为一个具体的数学问题，然后再来寻找算法解决。抽象的过程交给算法科学家了，抽象的结果是：寻找diff的过程可以被表示为图搜索

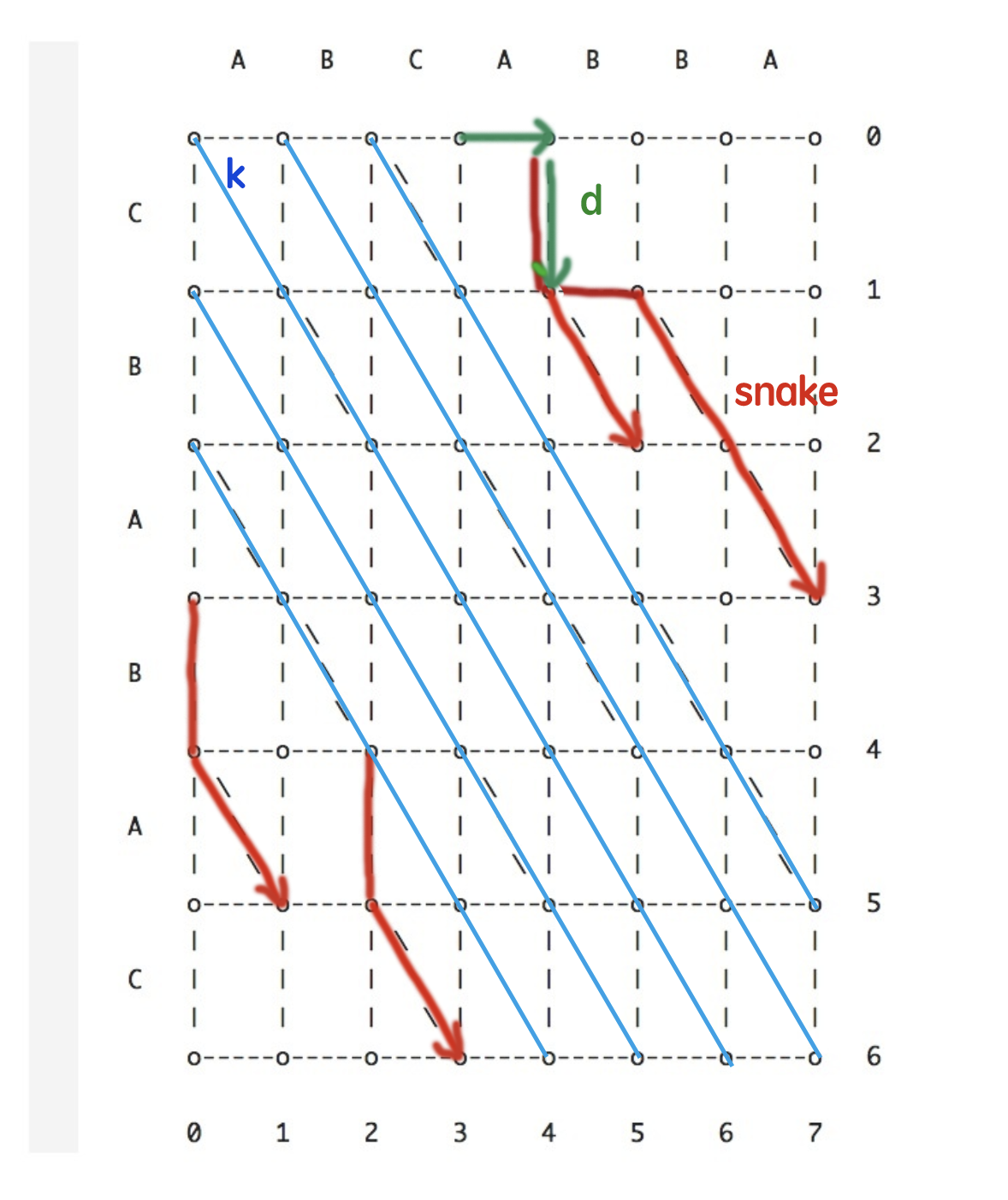
什么意思呢？还是以两个字符串，src=ABCABBA，dst=CBABAC为例，根据这两个字符串我们可以构造下面一张图，横轴是src内容，纵轴是dst内容，那么图中每一条从左上角到右下角的路径，都表示一个diff。向右表示删除，向下表示新增，对角线则表示原内容保持不动

根据图中形成的线路，我们可以选择一条路径看看它的效果

现在，“寻找diff”这件事，被抽象成了“寻找图的路径”了。那么，“最短的直观的”diff对应的路径有什么特点呢？

  • 路径长度最短（对角线不算长度）

  • 先向右，再向下（先删除，后新增）

三个概念

根据 Myers 的论文，他提出了三个概念：

  • snake: 一条snake代表走一步。例如从(0,0)->(0,1) / (0,0)->(1,0) / (0,1)->(0,2)->(2,4) 这分别为三条snake，走对角线不计入步数。

  • k line: 定义 k = x - y （我们可以写成 y = x - k，是相同斜率的平行斜线组成的一个集合)

  • d contour: 走一步算一个d

算法原理

根据路径图与提出的三个概念，我们可以画出如下一张图，横坐标代表d（步数），纵坐标代表k（偏移），图中每一点代表最优坐标

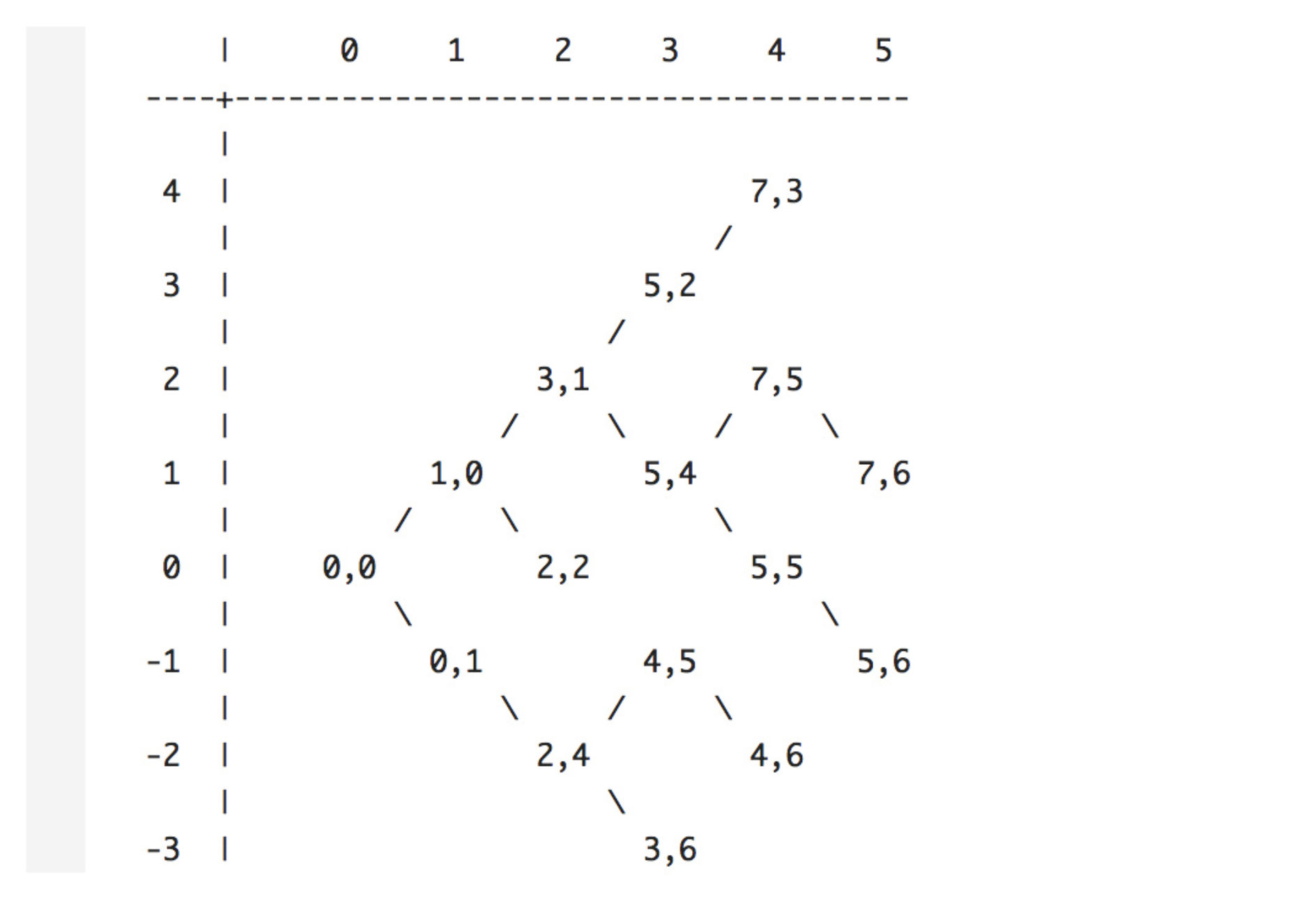
现在我们可以知道，其实Myers算法是一个典型的动态规划算法，也就是说，父问题的求解归结为子问题的求解。要知道d=5时所有k对应的最优坐标，必须先要知道d=4时所有k对应的最优坐标，要知道d=4时的答案，必须先求解d=3，以此类推

根据上图，我们也能直观的看到到达（7，6）的最短路径，见下图

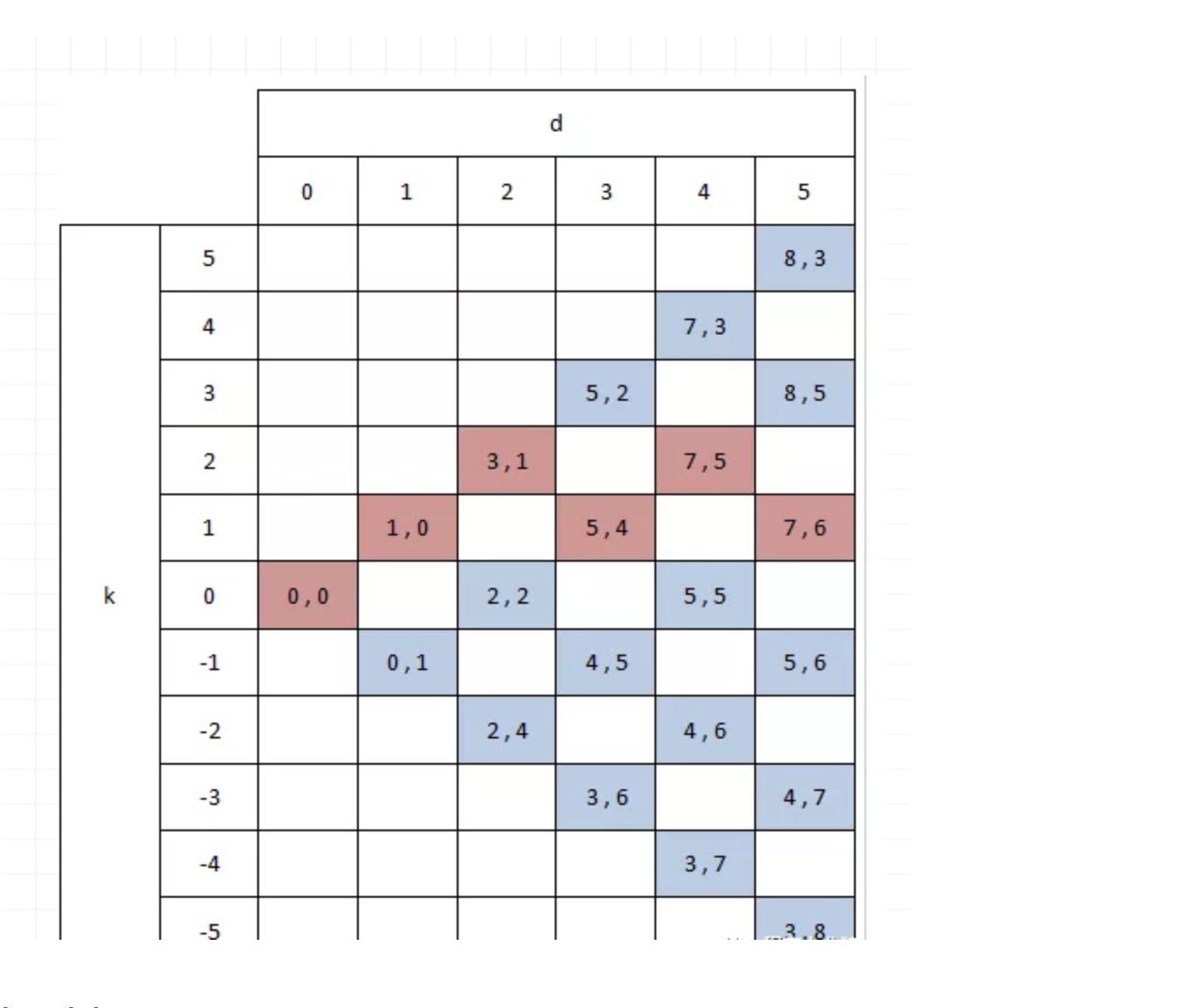
算法实现（java）

外层循环步数d，内层循环偏移k，两个for循环找出最短diff路径

  • 定义抽象基础节点PathNode，及实现类DiffNode（做操作的节点），Snake（对角线节点）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

public abstract class PathNode {
    public final int i;
    public final int j;
    public final PathNode prev;

    public PathNode(int i, int j, PathNode prev) {
        this.i = i;
        this.j = j;
        this.prev = prev;
    }

    public abstract Boolean isSnake();

    @Override
    public String toString() {
        StringBuffer buf = new StringBuffer("[");
        PathNode node = this;
        while (node != null) {
            buf.append("(");
            buf.append(Integer.toString(node.i));
            buf.append(",");
            buf.append(Integer.toString(node.j));
            buf.append(")");
            node = node.prev;
        }
        buf.append("]");
        return buf.toString();
    }
}

public final class Snake extends PathNode {
    public Snake(int i, int j, PathNode prev) {
        super(i, j, prev);
    }

    @Override
    public Boolean isSnake() {
        return true;
    }
}

public final class DiffNode extends PathNode {
    public DiffNode(int i, int j, PathNode prev) {
        super(i, j, prev);
    }

    @Override
    public Boolean isSnake() {
        return false;
    }
}
  • 寻找最优路径 及 解析diff
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118

public class MyersDiff<T> {
    /**
     * 默认相等规则
     */
    private final Equalizer<T> DEFAULT_EQUALIZER = (original, revised) -> original.equals(revised);
    private final Equalizer<T> equalizer;

    public MyersDiff() {
        equalizer = DEFAULT_EQUALIZER;
    }

    public MyersDiff(Equalizer<T> equalizer) {
        this.equalizer = equalizer;
    }
    /**
     * 寻找最优路径
     */
    public PathNode buildPath(List<T> orig, List<T> rev) throws Exception {
        if (orig == null)
            throw new IllegalArgumentException("original sequence is null");
        if (rev == null)
            throw new IllegalArgumentException("revised sequence is null");
        final int N = orig.size();
        final int M = rev.size();
        //最大步数（先全减后全加）
        final int MAX = N + M + 1;
        final int size = 1 + 2 * MAX;
        final int middle = size / 2;
        //构建纵坐标数组（用于存储每一步的最优路径位置）
        final PathNode diagonal[] = new PathNode[size];
        //用于获取初试位置的辅助节点
        diagonal[middle + 1] = new Snake(0, -1, null);
        //外层循环步数
        for (int d = 0; d < MAX; d++) {
            //内层循环所处偏移量，以2为步长，因为从所在位置走一步，偏移量只会相差2
            for (int k = -d; k <= d; k += 2) {
                //找出对应偏移量所在的位置，以及它上一步的位置（高位与低位）
                final int kmiddle = middle + k;
                final int kplus = kmiddle + 1;
                final int kminus = kmiddle - 1;
                //若k为-d，则一定是从上往下走，即i相同
                //若diagonal[kminus].i < diagonal[kplus].i，则最优路径一定是从上往下走，即i相同
                int i;
                PathNode prev;
                if ((k == -d) || (k != d && diagonal[kminus].i < diagonal[kplus].i)) {
                    i = diagonal[kplus].i;
                    prev = diagonal[kplus];
                } else {
                    //若k为d，则一定是从左往右走，即i+1
                    //若diagonal[kminus].i = diagonal[kplus].i，则最优路径一定是从左往右走，即i+1
                    i = diagonal[kminus].i + 1;
                    prev = diagonal[kminus];
                }
                //根据i与k，计算出j
                int j = i - k;
                //上一步的低位数据不再存储在数组中（每个k只清空低位即可全部清空）
                diagonal[kminus] = null;
                //当前是diff节点
                PathNode node = new DiffNode(i, j, prev);
                //判断被比较的两个数组中，当前位置的数据是否相同，相同，则去到对角线位置
                while (i < N && j < M && equals(orig.get(i), rev.get(j))) {
                    i++;
                    j++;
                }
                //判断是否去到对角线位置，若是，则生成snack节点，前节点为diff节点
                if (i > node.i)
                    node = new Snake(i, j, node);
                //设置当前位置到数组中
                diagonal[kmiddle] = node;
                //达到目标位置，返回当前node
                if (i >= N && j >= M) {
                    return diagonal[kmiddle];
                }
            }
        }
        throw new Exception("could not find a diff path");
    }

    private boolean equals(T orig, T rev) {
        return equalizer.equals(orig, rev);
    }

    /**
     * 打印diff
     */
    public void buildDiff(PathNode path, List<T> orig, List<T> rev) {
        List<String> result = new ArrayList<>();
        if (path == null)
            throw new IllegalArgumentException("path is null");
        if (orig == null)
            throw new IllegalArgumentException("original sequence is null");
        if (rev == null)
            throw new IllegalArgumentException("revised sequence is null");
        while (path != null && path.prev != null && path.prev.j >= 0) {
            if (path.isSnake()) {
                int endi = path.i;
                int begini = path.prev.i;
                for (int i = endi - 1; i >= begini; i--) {
                    result.add("  " + orig.get(i));
                }
            } else {
                int i = path.i;
                int j = path.j;
                int prei = path.prev.i;
                if (prei < i) {
                    result.add("- " + orig.get(i - 1));
                } else {
                    result.add("+ " + rev.get(j - 1));
                }
            }
            path = path.prev;
        }
        Collections.reverse(result);
        for (String line : result) {
            System.out.println(line);
        }
    }
}
  • 测试及结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14

public static void main(String[] args) {
    String oldText = "A\nB\nC\nA\nB\nB\nA";
    String newText = "C\nB\nA\nB\nA\nC";
    List<String> oldList = Arrays.asList(oldText.split("\\n"));
    List<String> newList = Arrays.asList(newText.split("\\n"));
    MyersDiff<String> myersDiff = new MyersDiff<>();
    try {
        PathNode pathNode = myersDiff.buildPath(oldList, newList);
        System.out.println(pathNode);
        myersDiff.buildDiff(pathNode, oldList, newList);
    } catch (Exception e) {
        e.printStackTrace();
    }
}

1
2
3
4
5
6
7
8
9
10

[(7,6)(7,5)(6,4)(5,4)(3,2)(3,1)(2,0)(1,0)(0,0)(0,-1)]
- A
- B
  C
+ B
  A
  B
- B
  A
+ C

注意

在git中不只是有增加和删除，还有修改，修改的原理是同时出现增加和删除，即为修改

时间复杂度

传统diff使用的是最naive的LSC计算算法（LCS:最长公共子序列），时间复杂度是O(M*N)（M,N分别为src与target的序列长度）

Myers的diff算法更好，时间复杂度为O((M+N)*D)（D为src与target的距离长度）尤其是在src与target相近时时间复杂度接近O(M+N)

延伸：动态规划

差分算法是典型的动态规划算法，动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决

1

动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解

例子一

我们有个题目：有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

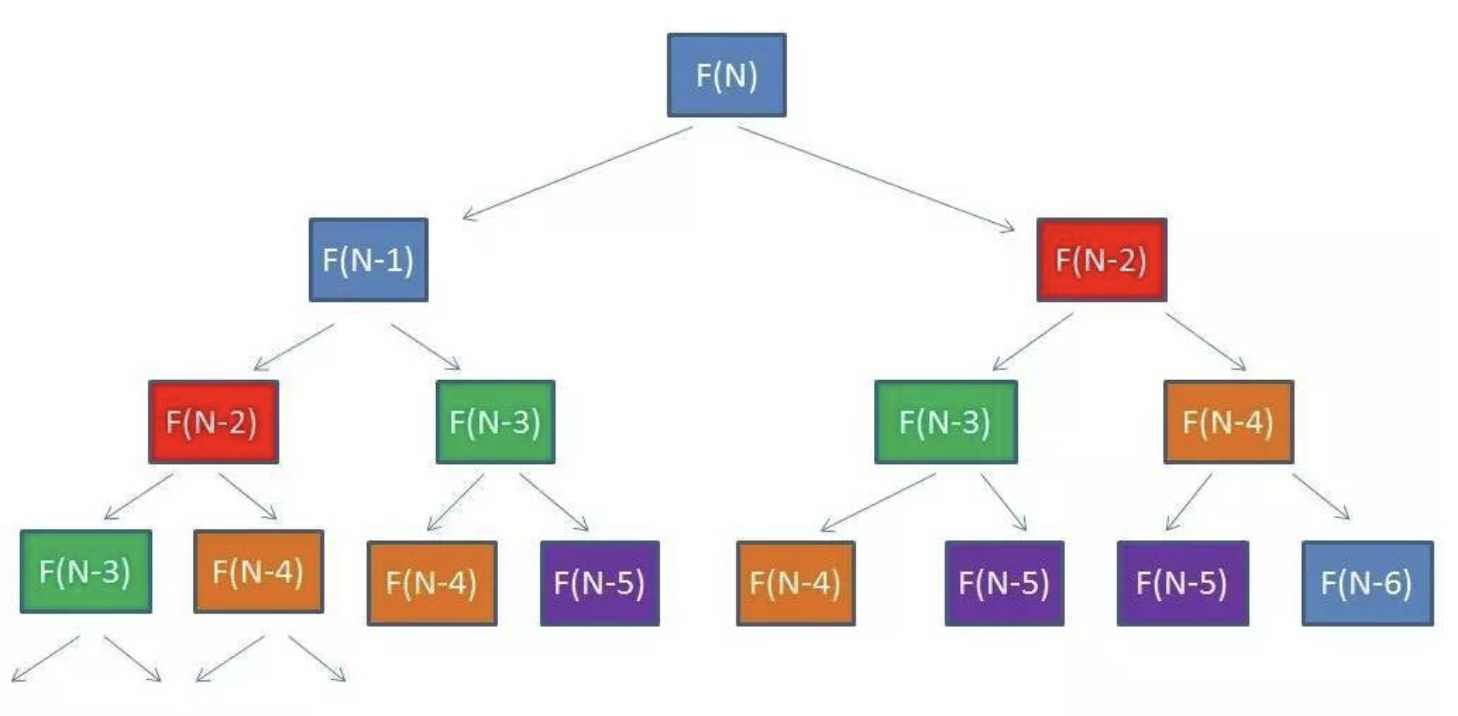
根据题目我们可以确定F(10)=F(8)+F(9)，即：从0到10级台阶的走法数量=从0到8级台阶的走法数量+从0到9级台阶的走法数量，则可推出如下公式：

1
2
3

F(1) = 1
F(2) = 2
F(n) = F(n-1)+F(n-2)（n>=3）

重要概念

  • 最优子结构：F(8)和F(9)是F(10)的最优子结构

  • 边界：F(1)和F(2)是问题的【边界】，如果一个问题没有边界将永远无法得到有限的结果

  • 状态转移方程：F(n)=F(n-1)+F(n-2)是阶段与阶段之间的【状态转移方程】，这是动态规划的核心，决定了问题的每一个阶段和下一阶段的关系

实现逻辑

  • 方法一：递归求解，时间复杂度：O(N^2）

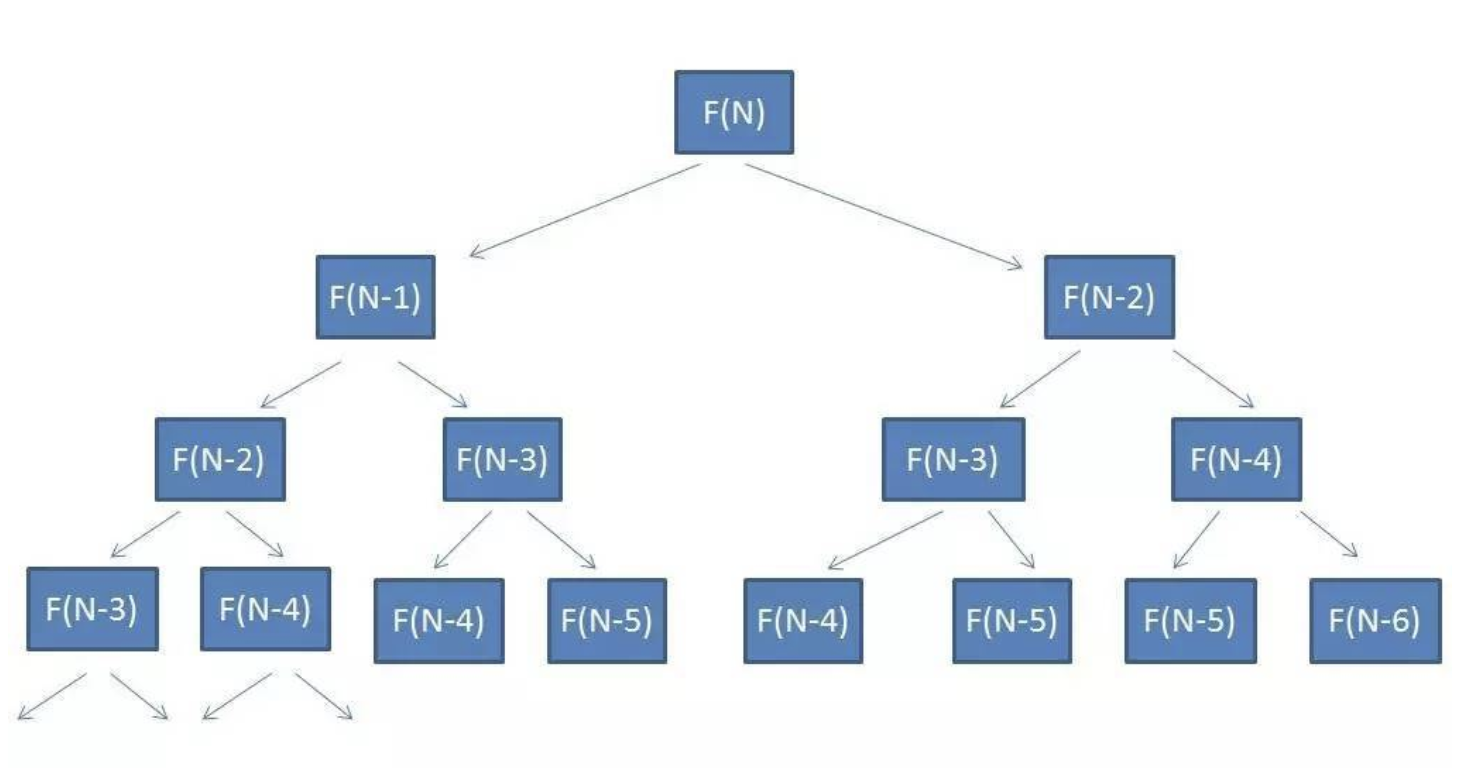
  • 方法二：备忘录算法，缓存已经计算过的值，时间复杂度：O(N)，空间复杂度：O(N)

  • 方法三：思路逆转，从底往上算，每次只需要存储前一次的值，时间复杂度：O(N)，空间复杂度：O(1)

测试狂人
关注
  • 6
    点赞
  • 踩
  • 16
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
myers-diff-cpp:C ++中的Myers差分算法
04-01
myers-diff-cpp C ++中的Myers差分算法 仅翻译“ find_middle_snake_myers_original”方法。 仅适用于比较整数数组。 这是直接从翻译而来 所有学分归原始作者所有。
git_diff_parser：Crystal中的Git Diff解析器
02-04
本文将深入探讨`git_diff_parser`的相关知识点，包括其工作原理、主要功能以及如何在Crystal项目中使用。 1. **Git Diff基础知识** Git diff是Git用来比较文件或目录差异的命令。它显示两个版本之间的差异，包括...
手动实现 git 的 git diff 功能
heshiyuan1406146854的博客
11-24 1159
这是 git diff 后的效果，感觉挺简单的，不就是 比较新旧版本，新增了就用 "+" 显示新加一行，删除了就用 "-" 显示删除一行，修改了一行就用 "-"、"+" 显示将旧版本中的该行干掉了并且新版本中增加了一行，即使用 "删除" + "新增" 操作代替 "修改" 操作。1. 最开始 index_old = index_new = 7，算法检测到新旧版本的第7行的内容相同( 后面我们就尽量用伪代码表示，就不说这么多啰里啰嗦的话了 )，即 lines_old[ 7] = lines_new[ 7]。
Git Diff 算法——Myers算法
t949500898的博客
09-06 2694
diff 是我们每天都要使用的一个功能，每次提交时，我都习惯先用 git diff --cached 看看这次提交更改了些什么，确定没问题，然后再 git commit。git 生成的 diff 非常直观，直观到我从来都没有去思考过 diff 是怎么生成的，觉得这应该是很简单的一件事，两个文件做个对比，不就行了。 什么是直观的 diff 我们先简单定义一下什么是 diff：diff 就是目标文本和源文本之间的区别，也就是将源文本变成目标文本所需要的操作。 git 为我们生成的 di...
Myers‘Diff之贪婪算法
stven_king的专栏
10-10 2410
Myers’ Diff 前言 写这篇文章已经拖了很久了，因为一直在看它后续的 Myers’ Diff 的变体 。最初不知道是什么时候发现 DiffUtil 对比列表 item 数据进行局部刷新，git 文件对比都用到了这个算法。上个月刚好再一次看到了就想深入了解一下。但发现发现国内的博客和帖子，对这个算法的讲述内容比较少，每篇文章都讲述了作者自己认为重要的内容，所以有一个点搞不懂的话没法整体性的进行理解。刚开始我自己就有一个点没想清楚想了好几天，我觉得程序员不能怕算法，书读百遍其义自现，阅读算法代码也是如此
Myer差分算法（Myer's diff algorithm）
imred的专栏
04-03 4480
Myer差分算法是一个时间复杂度为O(ND)的diff算法，就以diff两个字符串为例，其中N为两个字符串长度之和，D为两个字符串的差异部分的总长度。这个算法首先发表在An O(ND) Difference Algorithm and Its Variations。 Myer差分算法直接解决的问题是最长公共子序列（LCS）的等价问题——最小编辑脚本（SES）问题。当然了，这是论文中的表述，在我看来...
git diff的生成方式：myers diff算法
许佳佳的博客
09-20 2245
概述 本文参考：https://blog.jcoglan.com/2017/02/12/the-myers-diff-algorithm-part-1/ 每个开发者多少都接触过git的diff功能，如下图： 该功能能够展示出某个文件的改动信息，非常便于开发者的日常开发。 本文将探讨下此功能实现的原理。 myers diff 做了啥 引用个例子 a = ABCABBA b = CBABAC 现在要找出ab之间的diff。仔细想一想，我们会发现其实两者之间的diff情况是有无数个的，比如可以找到以下几
bsdiff差分算法最新版.7z
04-26
bsdiff差分算法是一种高效的文件补丁生成与应用工具，主要用在软件更新和系统升级领域，特别是对于嵌入式设备或下位机系统。它由Christoph Holzmayer开发，通过对比两个文件，生成一个补丁文件，使得只用较小的传输...
git-diff-blame：:detective:在blame信息旁边显示diff，例如author和commit
02-03
`git-diff-blame`是Git的一个扩展工具，它结合了`git blame`和`git diff`的功能，为开发者提供了一种更为直观的方式来追踪代码历史。在这个工具的帮助下，开发者可以更方便地了解代码的修改历史以及是谁在何时进行了...
git-difftool:围绕“git diff”的 Python 包装器，方便查看更改
07-13
git-difftool 围绕“git diff”的 Python 包装器，方便查看更改 执照 在 Boost 软件许可下分发，版本 1.0。 （请参阅随附文件 LICENSE_1_0.txt 或复制到 ） 兼容性 需要 Git 1.7.2 或更高版本。 我在 cygwin 和 ...
atom-git-difftool:在.gitconfig中配置的差异工具中打开当前项目
04-30
Git Difftool 在.gitconfig中配置的差异工具中打开当前项目或文件。 基本上，它在当前项目上运行git difftool 。 用法 从命令面板运行Git Difftool: Diff File差异Git Difftool: Diff File ，或使用⌥⌃D差异当前...
Myers差分算法
JenKin的博客
05-28 777
本文参考了文章： 简析Myers 在参考文章中我对Myers差分算法有了一定的理解，但是在代码实现的过程中还是会遇到很多问题，而作者对源码的解释比较少，因此我着重于对实现过程做一个分析。 概述 我把代码的实现分为了三个部分： 绘制编辑图 生成snake 回溯snake 绘制编辑图 下图是原论文里面的编辑图，我们需要吧圈起来的点对应的保存下来，保存的方式类似下面的表格 在这张表格里面表示了k线和步数d之间的关系 具体的代码实现可以参考论文里面的伪代码 private static void my.
git commit后，如何撤销commit
Zero .
07-16 5631
修改了本地的代码，然后使用： git add file git commit -m '修改原因' 执行commit后，还没执行push时，想要撤销这次的commit，该怎么办？ 解决方案： 使用命令： git reset --soft HEAD^ 这样就成功撤销了commit，如果想要连着add也撤销的话，--soft改为--hard（删除工作空间的改动代码）。 命令详解： HEAD^ 表示上一个版本，即上一次的commit，也可以写成HEAD~1 如果进行两次的commit，想要都
编辑距离：最长公共子序列-LCS问题
gongdiwudu的专栏
01-14 4795
最长公共子序列（LCS）问题是在一组序列（通常只有两个序列）中找到所有序列共有的最长子序列的问题。它与最长公共子串问题不同：与子串不同，子序列不需要占据原始序列中的连续位置。最长公共子序列问题是经典的计算机科学问题，是 diff 实用程序等数据比较程序的基础，在计算语言学和生物信息学中有应用。它还被 Git 等版本控制系统广泛用于协调对受版本控制的文件集合所做的多项更改。 例如，考虑序列 (ABCD) 和 (ACBAD)。它们有 5 个长度为 2 的公共子序列：(AB)、(AC)、(AD)
Diff算法
陈开心的博客
09-29 2139
diff算法并不是由react或者Vue或者虚拟dom提出的一个最新的概念，它是Linux的基础命令，在git代码管理工具中，在网上在线对比文件的工具中都有这个算法的应用，这个算法早就在我们身边了。在vdom中又被用来对比两个虚拟dom的节点，在vdom中应用diff算法是为了找出需要更新的节点，对比的原理和对比字符串是一样的。 vdom使用diff算法的原因： DOM操作是昂贵的，应尽量减少D...
git 导出差异 diff 文件
热门推荐
weixin_44021334的博客
05-27 1万+
git 下，做了修改的文件， git diff 可以看到修改前后的差异。 修改后，常常需要导出修改差异文件，如 a.diff 、b.path 。 记录下导出命令。 1.导出本地修改的 diff 本地修改了文件，还没有 git add ，可以这样导出。 格式为： git diff 【修改的文件或文件夹】>>【差异文件名称】 示例， git diff device.mk >> device.diff git diff device.mk >> device.pacth d
git深入理解(三)：git diff详解
猛犸象
12-08 2221
Show changes between commits, commit and working tree, etc 是一个用来查看差异的工具。 查看帮助 $ git diff -h usage: git diff [<options>] [<commit> [<commit>]] [--] [<path>...] 信息量过少 比较工作区和暂存区的差别 git diff 比较暂存区和本库的差别 git diff --cached 比较工作区和版本库的
diff git 代码实现_Git diff 算法
weixin_42390070的博客
01-17 1026
在Git中，有四种diff算法，即Myers，Minimal，Patience和Histogram。默认Myers。Minimal是Myers的改进，Histogram是Patience的改进。Myers总是通过完全相同的行来实现匹配，它的问题在于可能会有大量的空行和括号影响结果。Histogram通过“少量的独特的行”做锚定，来更合适的标记代码段的移动。Myers算法我觉得这个文章讲的非常好：h...
diff工具的实现原理
wenqibiao8的专栏
06-24 2596
http://blog.sina.com.cn/s/blog_6b8b431d0100xiow.html http://blog.csdn.net/fallenorc/article/details/372716
git 生成diff
最新发布
05-18
在git中，diff命令用于比较不同版本之间的差异。生成diff的基本格式为： ``` git diff <source_branch> <target_branch> ``` 其中，`source_branch`表示源分支，`target_branch`表示目标分支。执行该命令后，会输出源分支和目标分支之间的差异，包括文件内容、文件名等。如果不指定分支，则默认为当前分支和HEAD之间的差异。 除了上述基本用法，还可以使用一些选项来生成不同形式的diff： 1. `--color-words`：使用颜色高亮显示不同之处 2. `--stat`：仅显示差异文件的统计信息 3. `--name-only`：仅显示有差异的文件名 4. `--name-status`：显示差异文件的状态（新增、修改、删除等） 如果要将diff输出到文件中，可以使用重定向符号`>`，例如： ``` git diff source_branch target_branch > diff.txt ``` 这样就会将diff输出到名为`diff.txt`的文件中。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值