这里有一个由 Marsaglia 首创 Knuth 推荐的方法:
#include <stdlib.h>
#include <math.h>
double gaussrand()
{
static double V1, V2, S;
static int phase = 0;
double X;
if(phase == 0) {
do {
double U1 = (double)rand() / RAND_MAX;
double U2 = (double)rand() / RAND_MAX;
V1 = 2 * U1 - 1;
V2 = 2 * U2 - 1;
S = V1 * V1 + V2 * V2;
} while(S >= 1 || S == 0);
X = V1 * sqrt(-2 * log(S) / S);
} else
X = V2 * sqrt(-2 * log(S) / S);
phase = 1 - phase;
return X;
}
以上代码是基于Box-Muller方法,基本思想是生成两组独立的随机数U和V,这两组数在(0,1]上均匀分布,用U和V生成两组独立的标准常态分布随机变量X和Y:
-
 。
。











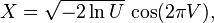














 770
770

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








