【算法-＞复杂度】时间复杂度与空间复杂度

最新推荐文章于 2024-07-10 14:43:32 发布

小明2766

最新推荐文章于 2024-07-10 14:43:32 发布

阅读量285

点赞数

分类专栏：算法与数据结构文章标签：算法 leetcode

原文链接：https://leetcode-cn.com/leetbook/detail/illustration-of-algorithm/

版权

算法与数据结构专栏收录该内容

8 篇文章 0 订阅

订阅专栏

转自https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/r84gmi/

本文针对原文简化了一些书写，并且加入了自己的理解。

算法复杂度

算法复杂度旨在计算在输入数据量 N 的情况下，算法的「时间使用」和「空间使用」情况；体现算法运行使用的时间和空间随「数据大小 N 」而增大的速度。

算法复杂度主要可从时间、空间两个角度评价：

时间：假设各操作的运行时间为固定常数，统计算法运行的「计算操作的数量」，以代表算法运行所需时间；
空间：统计在最差情况下，算法运行所需使用的「最大空间」；

「输入数据大小N」指算法处理的输入数据量；根据不同算法，具有不同定义，例如：

排序算法： N 代表需要排序的元素数量；
搜索算法： N 代表搜索范围的元素总数，例如数组大小、矩阵大小、二叉树节点数、图节点和边数等；

时间复杂度

概念定义

根据定义，时间复杂度指输入数据大小为 N 时，算法运行所需花费的时间。需要注意：

统计的是算法的「计算操作数量」，而不是「运行的绝对时间」。计算操作数量和运行绝对时间呈正相关关系，并不相等。算法运行时间受到「编程语言、计算机处理器速度、运行环境」等多种因素影响。例如，同样的算法使用 Python 或 C++ 实现、使用 CPU 或 GPU 、使用本地 IDE 或力扣平台提交，运行时间都不同。
体现的是计算操作随数据大小 N 变化时的变化情况。假设算法运行总共需要「 1 次操作」、「 100 次操作」，此两情况的时间复杂度都为常数级 O(1) ；需要「 N 次操作」、「 100N 次操作」的时间复杂度都为 O(N)。

符号表示

时间复杂度有最差、平均、最佳三种情况，符号分别为 O , Θ , Ω表示。

例子：为了找到数组中是否有7

def find_seven(nums):
    for num in nums:
        if num == 7:
            return True
    return False

最好情况为Ω(1) ，比如第1个数字就是7
最差情况为O(N)，比如所有数字都不是7，遍历了所有数字
平均情况 Θ，需要考虑输入数据的分布情况，计算所有数据情况下的平均时间复杂度；例如本题目，需要考虑数组长度、数组元素的取值范围等；

大 O 是最常使用的时间复杂度评价渐进符号，下文示例与本 LeetBook 题目解析皆使用 O 。

常见种类

根据从小到大排列，常见的算法时间复杂度主要有：

$O(1)<O(logN)<O(N)<O(NlogN)<O(N^2 )<O(2^N )<O(N!)$

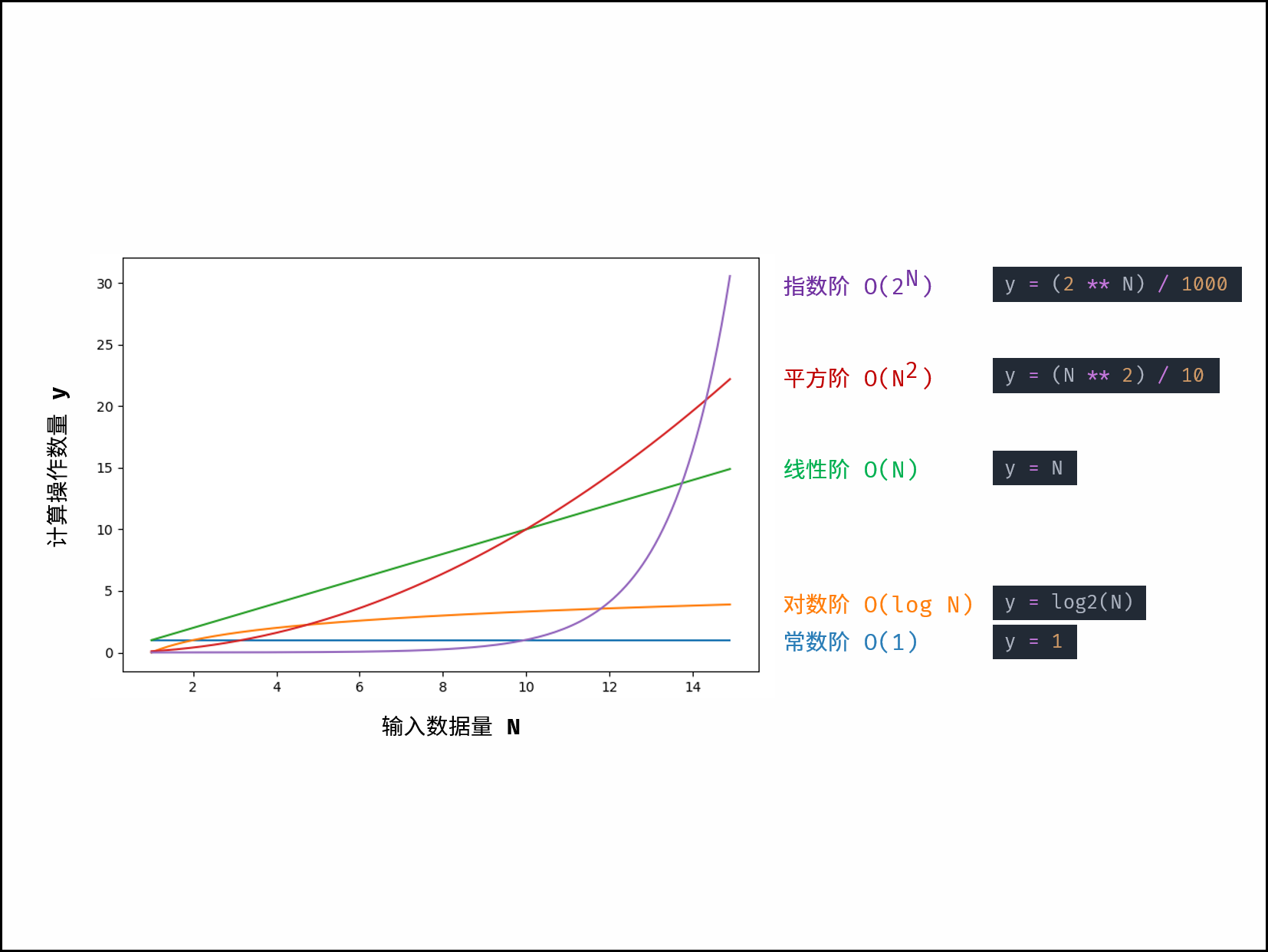
常数O(1)

运行次数与 NN 大小呈常数关系，即不随输入数据大小 NN 的变化而变化。

def algorithm(N):
    a = 1
    b = 2
    x = a * b + N
    return 1
#或者
def algorithm(N):
    count = 0
    a = 10000
    #循环与N无关
    for i in range(a):
        count += 1
    return count

线性O(N)

循环运行次数与 N 大小呈线性关系，时间复杂度为O(N) 。

def algorithm(N):
    count = 0
    for i in range(N):
        count += 1
    return count
#或者
def algorithm(N):
    count = 0
    a = 10000
    for i in range(N):
        #循环与N无关
        for j in range(a):
            count += 1
    return count

平方O(N²)

两层循环相互独立，都与 N 呈线性关系，因此总体与 N 呈平方关系，时间复杂度为 O(N²) 。

def algorithm(N):
    count = 0
    for i in range(N):
        for j in range(N):
            count += 1
    return count
#或者
#冒泡排序
def bubble_sort(nums):
    N = len(nums)
    #复杂度为O(N)
    for i in range(N - 1):
        #从n-1次到1次，平均循环次数为1，2，...，(n-1) = n/2，复杂度为O(N)
        for j in range(N - 1 - i):
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
    return nums

指数O(2^N)

生物学科中的细胞分裂即是指数级增长。初始状态为1个细胞，分裂一轮后为2个，分裂两轮后为4个，…，分裂N轮后有2^N个细胞。算法中，指数阶常出现于递归。

def algorithm(N):
    if N <= 0: return 1
    #计算1个-N 变成 计算2个-N-1
    count_1 = algorithm(N - 1)
    count_2 = algorithm(N - 1) 
    return count_1 + count_2

阶乘O(N!)

阶乘阶对应数学上常见的 “全排列” 。即给定 N 个互不重复的元素，求其所有可能的排列方案，则方案数量为：

$N \times (N - 1) \times (N - 2) \times \dots \times 2 \times 1 = N!$

阶乘常使用递归实现,算法原理:第一层分裂出 N 个，第二层分裂出 N−1 个，…，直至到第N层时终止并回溯。

def algorithm(N):
    if N <= 0: return 1
    count = 0
    #N的时候，需要递归N次；N-1的时候，需要递归N-1次；...；1的时候，需要递归1次
    #因此需要N*N-1*...*1 = N!
    for _ in range(N):
        count += algorithm(N - 1)
    return count

对数O(logN)

对数阶与指数阶相反，指数阶为 “每轮分裂出两倍的情况” ，而对数阶是 “每轮排除一半的情况” 。对数阶常出现于「二分法」、「分治」等算法中，体现着 “一分为二” 或 “一分为多” 的算法思想。

设循环次数为m，则输入数据大小N与 $2^m$ 呈线性关系，两边同时取 $log_2$ 对数，则得到循环次数m与 $log_2 N$ 呈线性关系，则时间复杂度为 $O (l o g N)$ 。

def algorithm(N):
    count = 0
    i = N
    while i > 1:
        #每次都将范围缩小1/2
        i = i / 2
        count += 1
    return count
#或
def algorithm(N):
    count = 0
    i = N
    a = 3
    while i > 1:
        #每次都将范围缩小1/a
        i = i / a
        count += 1
    return count

第2个的形式是m与 $log_a N$ 呈线性关系，时间复杂度为 $O(log_a N) = \frac{O(log_2 N)}{O(log_2 a)} = O(logN)$ 。

线性对数O(N logN)

两层循环相互独立，第一层和第二层时间复杂度分别为O(logN)和O(N)，则总体时间复杂度为O(N logN)

def algorithm(N):
    count = 0
    i = N
    while i > 1:
        #logN
        i = i / 2
        #N
        for j in range(N):
            count += 1
#嵌套为N logN

线性对数阶常出现于排序算法，例如「快速排序」、「归并排序」、「堆排序」等

示例题目

在这里插入图片描述

空间复杂度

概念定义

空间复杂度涉及的空间类型有：

输入空间：存储输入数据所需的空间大小；
暂存空间：算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；
输出空间：算法运行返回时，存储输出数据所需的空间大小；

通常情况下，空间复杂度指在输入数据大小为 N 时，算法运行所使用的**「暂存空间」+「输出空间」的总体大小**。

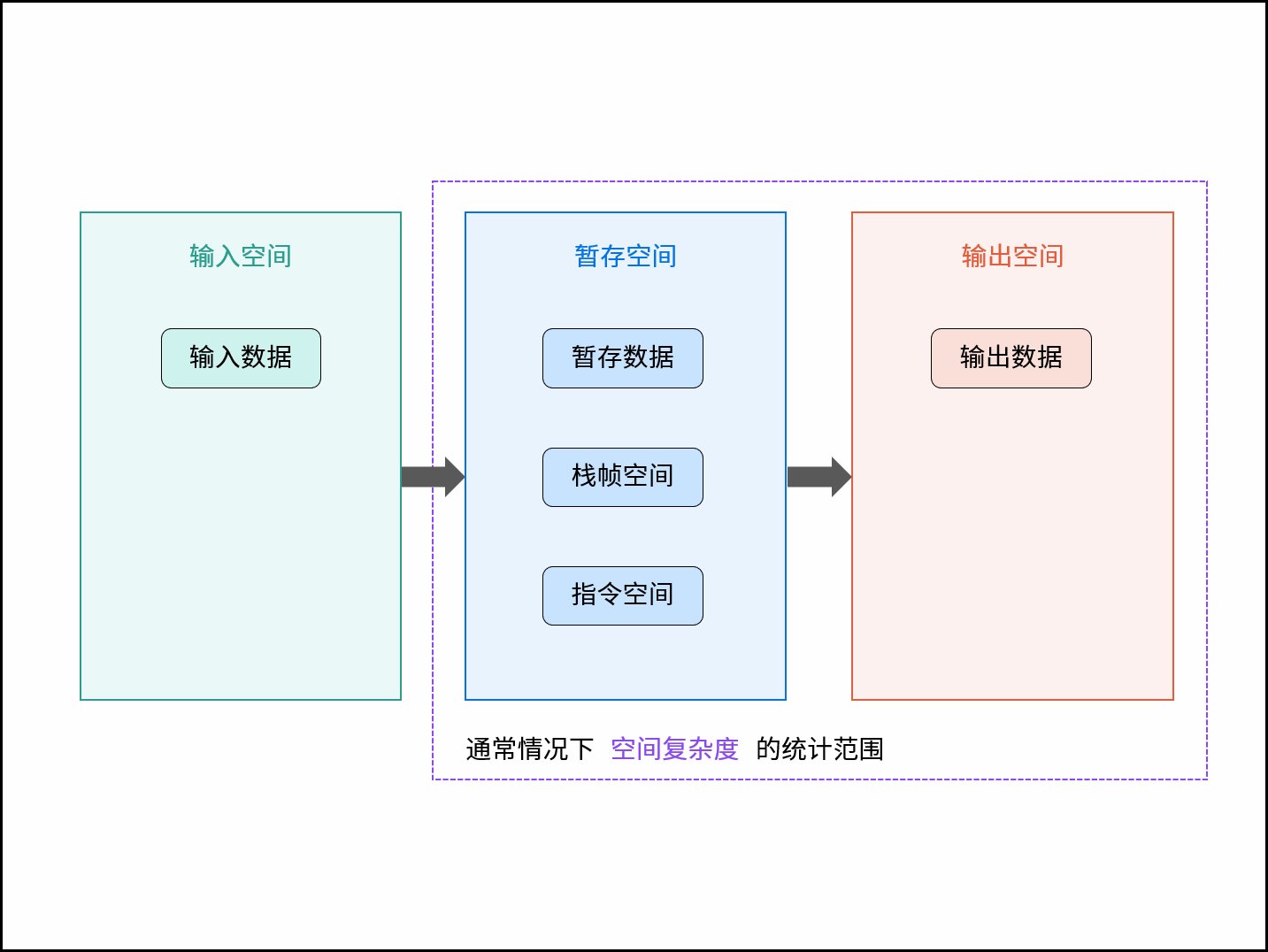
而根据不同来源，算法使用的内存空间分为三类：

暂存数据（数据空间）
栈帧空间
指令空间

指令空间：

编译后，程序指令所使用的内存空间。

数据空间：

算法中的各项变量使用的空间，包括：声明的常量、变量、动态数组、动态对象等使用的内存空间。

class Node:
    def __init__(self, val):
        self.val = val
        self.next = None

def algorithm(N):
    num = N         # 变量
    nums = [0] * N  # 动态数组
    node = Node(N)  # 动态对象

栈帧空间：

程序调用函数是基于栈实现的，函数在调用期间，占用常量大小的栈帧空间，直至返回后释放。如以下代码所示，在循环中调用函数，每轮调用 test() 返回后，栈帧空间已被释放，因此空间复杂度仍为O(1) 。

def test():
    return 0

def algorithm(N):
    for _ in range(N):
        test()

算法中，栈帧空间的累计常出现于递归调用。如以下代码所示，通过递归调用，会同时存在 N 个未返回的函数 algorithm() ，此时累计使用 O(N) 大小的栈帧空间。

def algorithm(N):
    if N <= 1: return 1
    return algorithm(N - 1) + 1

符号表示

通常情况下，空间复杂度统计算法在 “最差情况” 下使用的空间大小，以体现算法运行所需预留的空间量，使用符号 O 表示。

最差情况有两层含义，分别为「最差输入数据」、算法运行中的「最差运行点」。例如以下代码：


def algorithm(N):
    num = 5             # O(1)
    nums = [0] * 10     # O(1)
    if N > 10:
        nums = [0] * N  # O(N)

输入整数 N ，取值范围 N≥1 ；

最差输入数据：
- 当N≤10时，数组nums的长度恒定为10，空间复杂度为O(10)=O(1)；
- 当N>10时，数组nums长度为N，空间复杂度为O(N)；
- 因此，空间复杂度应为最差输入数据情况下的O(N)。
最差运行点：
- 在执行nums= [0] * 10时，算法仅使用O(1)大小的空间；
- 而当执行nums = [0] * N时，算法使用O(N)的空间；
- 因此，空间复杂度应为最差运行点的O(N)。

常见种类

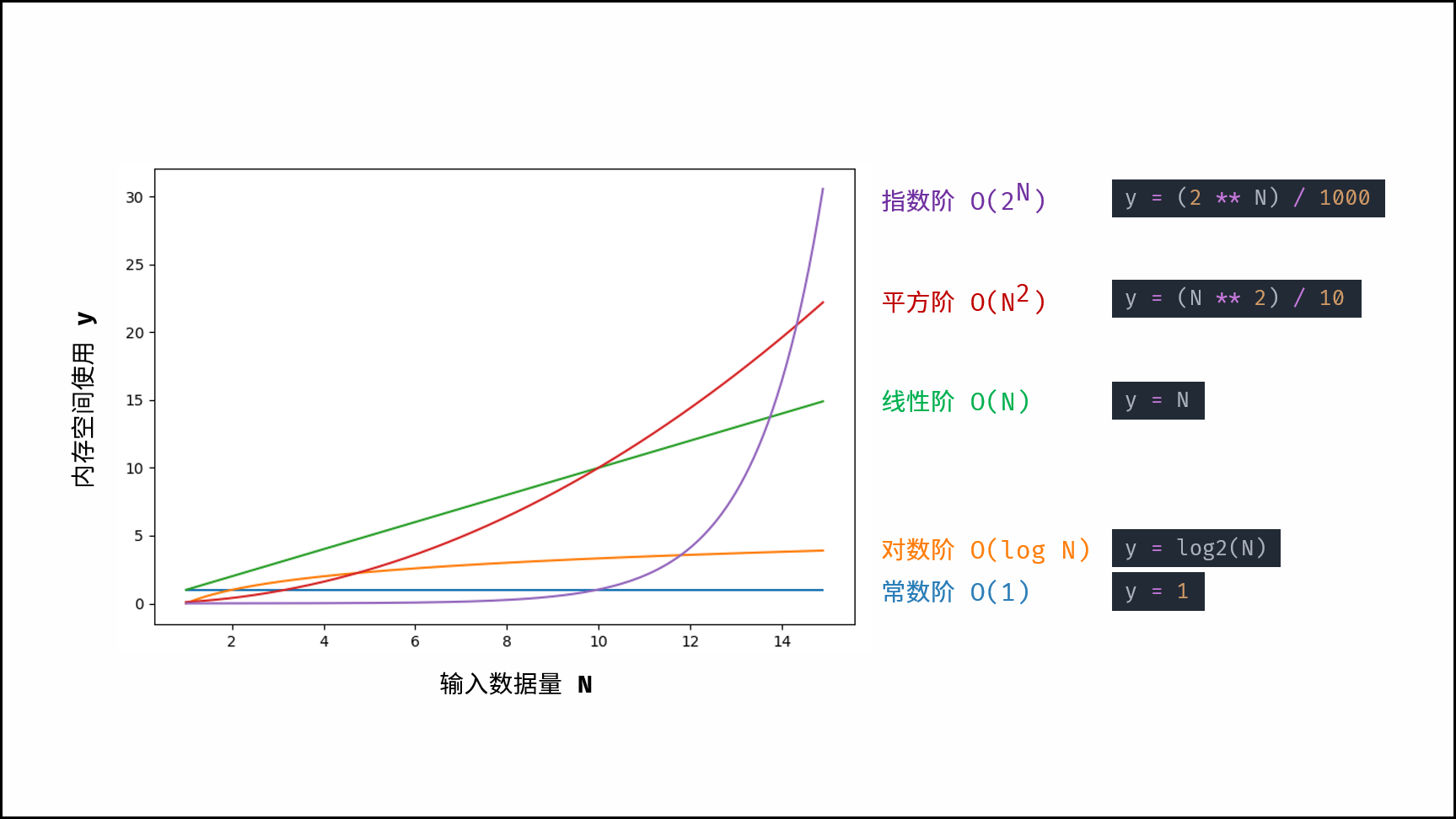
根据从小到大排列，常见的算法空间复杂度有：

$O(1)<O(logN)<O(N)<O(N^2 )<O(2^N )$

示例解析

示例节点类Node、函数test():

# 节点类 Node
class Node:
    def __init__(self, val):
        self.val = val
        self.next = None

# 函数 test()
def test():
    return 0

常数O(1)

普通常量、变量、对象、元素数量与输入数据大小 NN 无关的集合，皆使用常数大小的空间。

def algorithm(N):
    #这些初始化都与N无关
    num = 0
    nums = [0] * 10000
    node = Node(0)
    dic = { 0: '0' }
#或
def algorithm(N):
    for _ in range(N):
        #立即返回了，无累计栈帧空间使用，因此复杂度为O(1)
        test()

线性O(N)

元素数量与 N 呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等），皆使用线性大小的空间。

def algorithm(N):
    nums_1 = [0] * N
    nums_2 = [0] * (N // 2)

    nodes = [Node(i) for i in range(N)]
    
    dic = {}
    for i in range(N):
        dic[i] = str(i)
#或
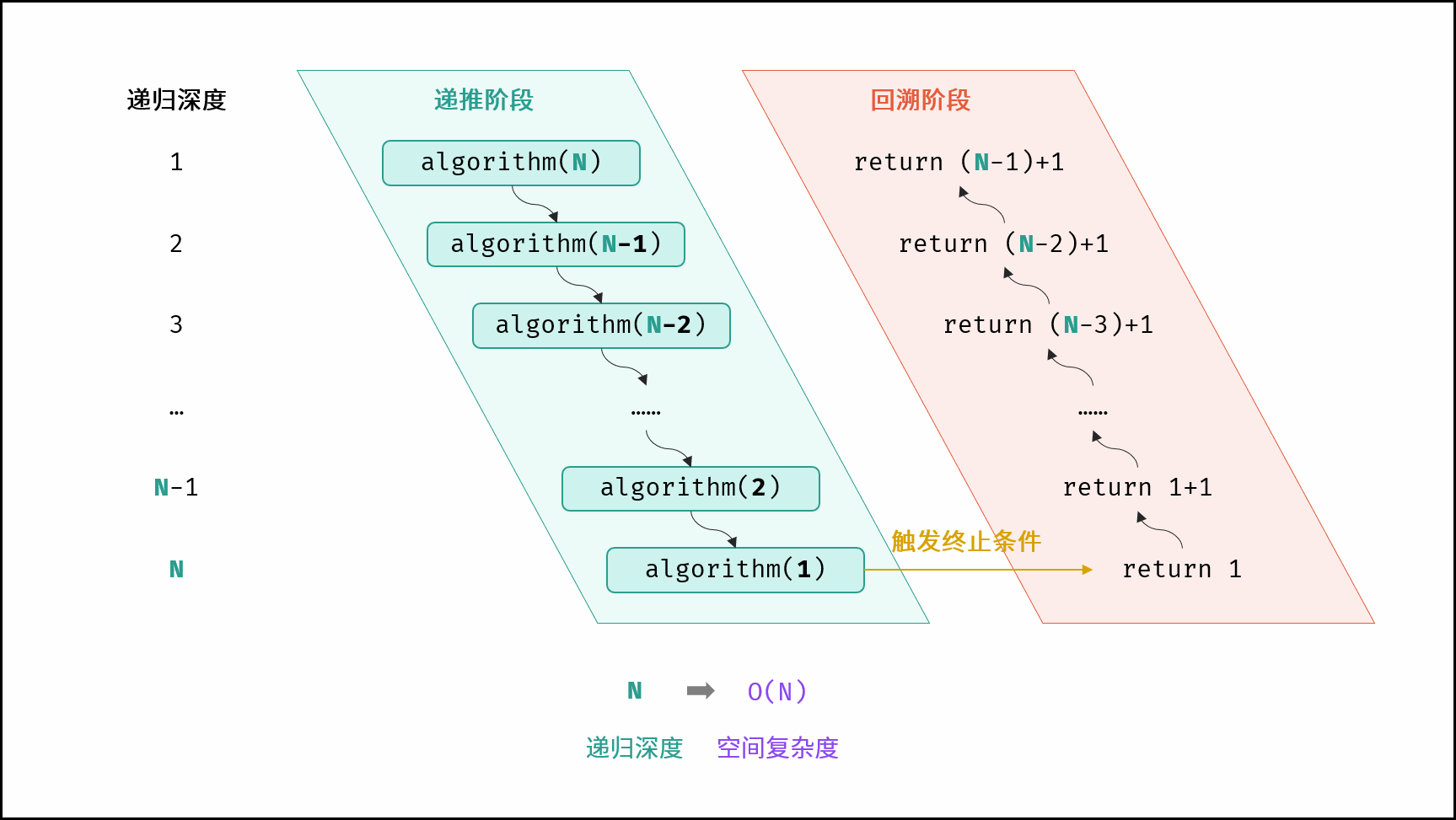
#此递归调用期间，会同时存在 N 个未返回的 algorithm() 函数，因此使用O(N) 大小的栈帧空间。
def algorithm(N):
    if N <= 1: return 1
    return algorithm(N - 1) + 1

如图，直到algorithm(1)才开始取消递归。

平方O(N²)

元素数量与 NN 呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。

def algorithm(N):
    #2维数组
    num_matrix = [[0 for j in range(N)] for i in range(N)]
    #2维数组
    node_matrix = [[Node(j) for j in range(N)] for i in range(N)]
#或
def algorithm(N):
    if N <= 0: return 0
    nums = [0] * N
    return algorithm(N - 1)

在第2个代码中：

递归调用时同时存在 N 个未返回的 algorithm() 函数，使用 O(N) 栈帧空间；
每层递归函数中声明了数组，平均长度为 $\frac{N}{2}$ ，使用 O(N) 空间；
因此总体空间复杂度为O(N²)。

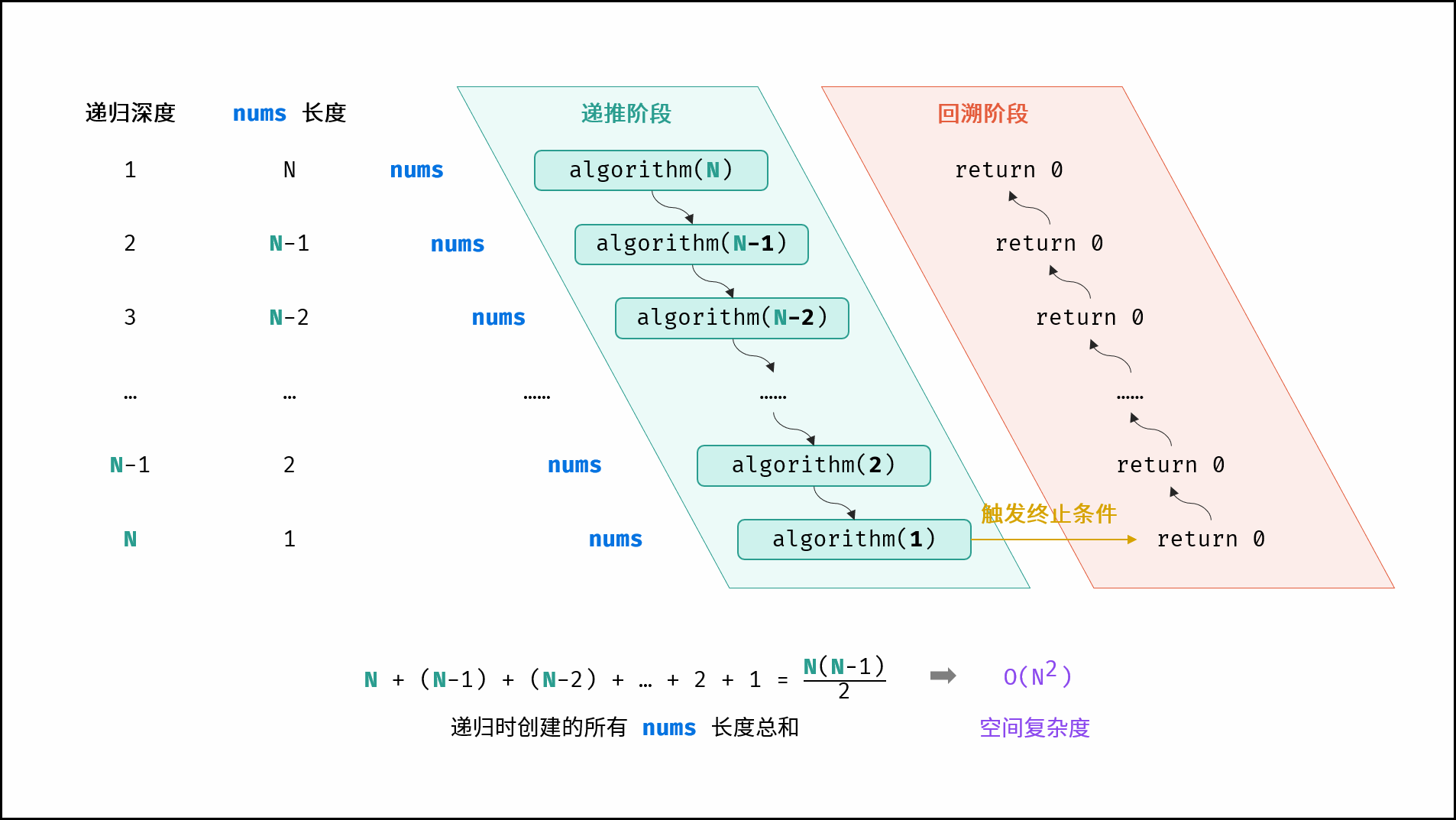
注意：这里是有两种解释。

如图所示，nums的长度总和为 $\frac{N(N-1)}{2}$ ，因此空间复杂度为O(N²)
每层递归中的数组平均长度为 $\frac{N}{2}$ ，比如1和N拼、2和N-1拼、3和N-2拼等…平均长度就为 $\frac{N}{2}$ 了，因此空间复杂度为O(N²)

指数O(2^N)

指数阶常见于二叉树、多叉树。

例如，高度为 N 的「满二叉树」的节点数量为2^N（图中是2^N层-1），占用 O(2^N) 大小的空间；
同理，高度为 N 的「满 m 叉树」的节点数量为 m^N ，占用O(m^N) = O(2^N)大小的空间。

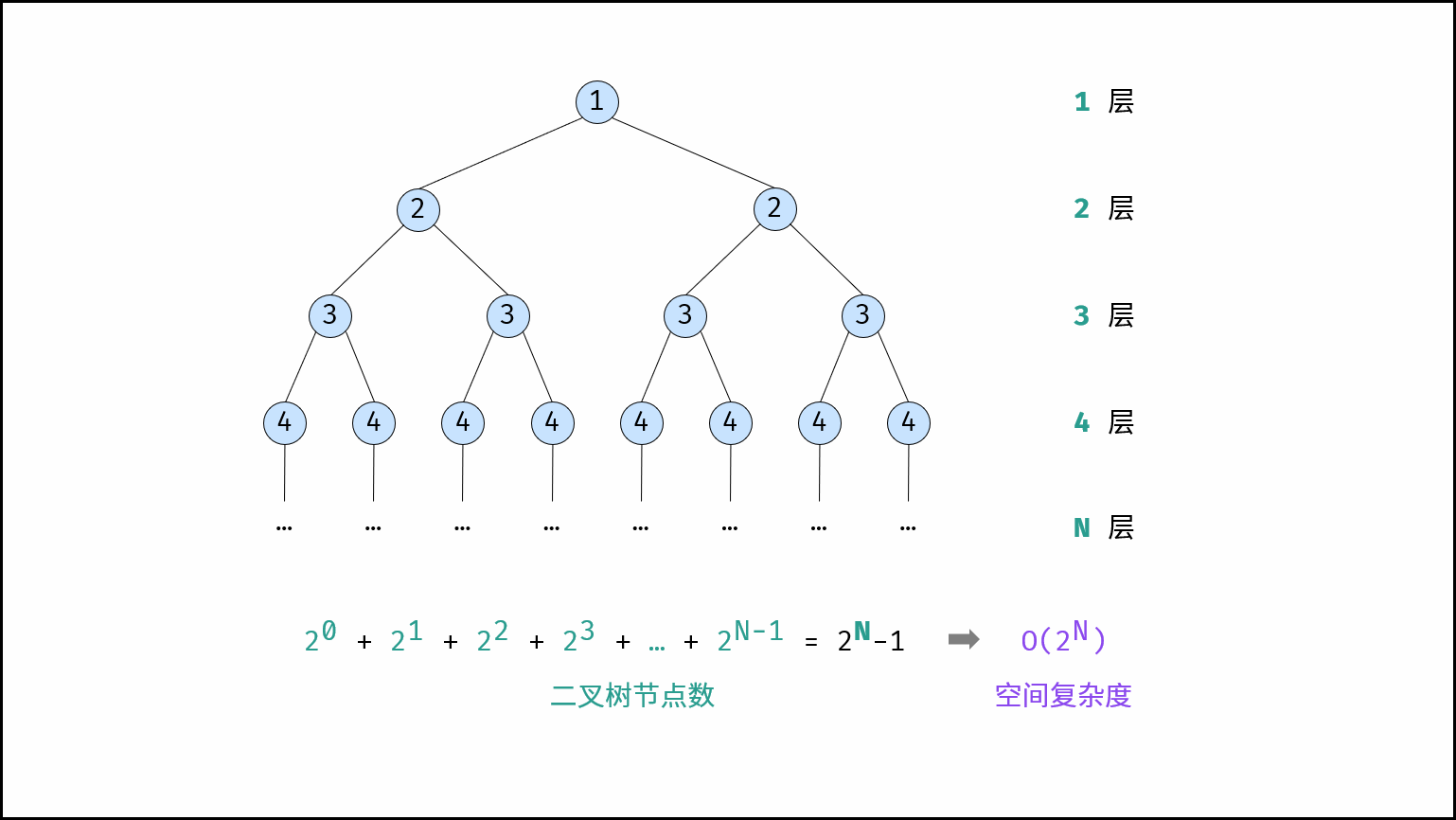
求和可以通过等比序列求和公式2算出来，满3叉树求和为 $3^0 + 3^1 + ... + 3^{N-1} = \frac{1*(1-3^N)}{1-3} = \frac{1}{2}(3^N -1)$ ，复杂度为 $O(3^N) = O(2^N)$

对数O(logN)

对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例如

快速排序，平均空间复杂度为Θ(logN)，最差空间复杂度为O(N)。拓展知识：通过应用 Tail Call Optimization ，可以将快速排序的最差空间复杂度限定至O*(N) 。
数字转化为字符串，设某正整数为N，则字符串的空间复杂度为O(logN)。推导如下：正整数N的位数为 $log_{10} N$ （个人理解准确来说为 $log_{10} N +1$ ，比如111是3位数），即转化的字符串长度为 $log_{10} N$ ，因此空间复杂度为O(logN)。

时空权衡

对于算法的性能，需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性，即时间和空间复杂度皆较低。而实际上，对于某个算法问题，同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度，往往是以提升空间复杂度为代价的，反之亦然。

由于当代计算机的内存充足，通常情况下，算法设计中一般会采取「空间换时间」的做法，即牺牲部分计算机存储空间，来提升算法的运行速度。

示例题目

在这里插入图片描述

小明2766

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【算法-＞复杂度】时间复杂度与空间复杂度

转自https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/r84gmi/本文针对原文简化了一些书写，并且加入了自己的理解。算法复杂度算法复杂度旨在计算在输入数据量 N 的情况下，算法的「时间使用」和「空间使用」情况；体现算法运行使用的时间和空间随「数据大小 N 」而增大的速度。算法复杂度主要可从时间、空间两个角度评价：时间：假设各操作的运行时间为固定常数，统计算法运行的「计算操作的数量」，以代表算法运行所需时.
复制链接

扫一扫