【小结】AC自动机

• 参考资料：http://blog.csdn.net/niushuai666/article/details/7002823
• 搞了两天，突然明白，这玩意它原来就是个$DFA$鸭！窝来分析分析

从$DFA$到$AC$自动机:

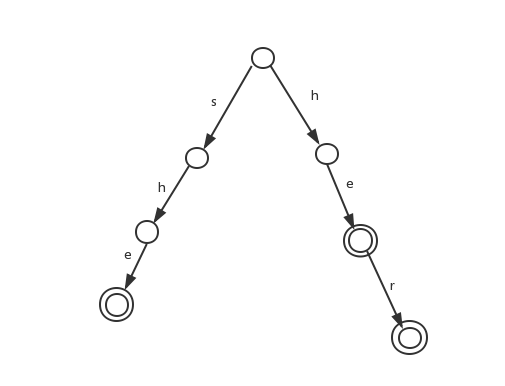
• 考虑以下单词: $\{she,\ he,\ her\}$，字母表$\sum$为$26$个小写字母

• 我们先画出它Trie树的模样
  

• 注意，双圈的是包含单词结尾的位置。然后我们尝试将它稍加改造，变成一个$DFA$！

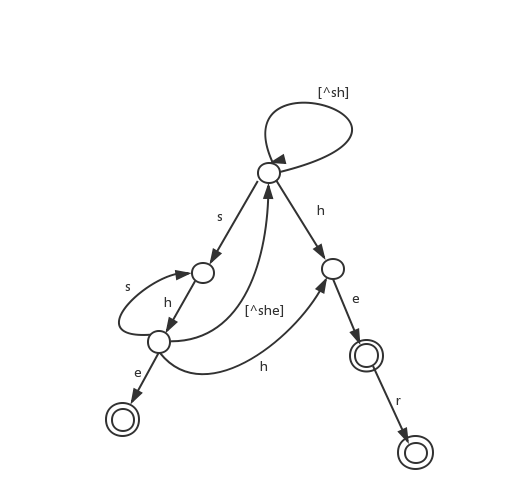
• 对每一个状态，必须补充下一个字母为其它（比如从起始状态出发，输入一个$h$，匹配上了，接下来输入可能为$a\sim z$，我们已经有了$e$的箭头，还要补上其它的）。这里是补上根节点和从根走$sh$的那个后的结果：
  
• 注意正则表达式$[\land sh]$表示除$s,h$外所有字母。我们考虑下面那个$sh$对应的状态，遇到$s$转到它的父节点，遇到$h$转到右边那个节点，遇到$e$到下面一个状态，遇到其它则直接转回起始状态。补充完余下的转移，完成后就可以拿来用了。比如我们拿到一个字符串，就可以想象自己就是这台$DFA$，每次读入一个字符，按照箭头的指示转至不同的状态，只要遇到了一个接受状态（图中双圈），就认为匹配上一次。我们发现，这台自动机已经可以完成我们要求的多模式匹配的任务了！也即通过对一堆串构造$DFA$，以后拿到一个串$M$，只需要每次读一个字符，然后走箭头，就可以完成$M$和这一大堆串的匹配～那么单次匹配的复杂度就只有$O(|M|)$了，这是线性的！
• 下面，稍加转化，就可以将上述$DFA$变成$AC$自动机。依然考虑左边这个$sh$对应的状态，如果遇到$e$，转到下面一个转态，不需要改变；但是如果遇到了$s$和$h$，我们并不是直接按照$s$和$h$的指示完成转换然后继续后面的匹配，而是保留这个$s$或者$h$，先转到起始状态，然后再重新读入$s$或者$h$继续匹配。也就是说，只要发生了“失配”，就转到另一个状态，继续处理。这么做的好处是容易在代码上实现。于是$sh$对应状态在遇到$s$或者$h$时，也会转向起始状态，这个转向就时$AC$自动机的所谓$fail$指针。在匹配时，用一个$tmp$指针模拟我们的手指，开始时指向起始状态，遇到$s$，就按照$s$箭头的指示移动到对应状态，直到所有字符都读完，匹配结束。
• 留个板子

/* **********************************************

  File Name: ac_automata.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月14日 星期五 08时41分23秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
const double EPS = 1e-8;
const double PI = acos(-1.0);

const int MAX = 500007;
const int MAXD = 26; //26 alphas
struct Trie {
    /* 
     * nxt & end is used in trie
     * fail is for ac automata
     */
    int nxt[MAX][MAXD], fail[MAX], end[MAX];
    int root, L; //root node, length(the nodes has been malloc)[0, L]
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L++] = 0;
        return L - 1;
    }
    void clear() {
        L = 0;
        root = newnode();
    }
    void insert(char* buf) {
        int len = strlen(buf);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][buf[i] - 'a'] == -1) {
                nxt[now][buf[i] - 'a'] = newnode();
            }
            now = nxt[now][buf[i] - 'a'];
        }
        ++end[now];
    }
    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    int query(char* buf, int len = -1) {
        if (len == -1) {
            len = strlen(buf);
        }
        int now = root;
        int res = 0;
        for (int i = 0; i < len; ++i) {
            now = nxt[now][buf[i] - 'a'];
            int tmp = now;
            while (tmp != root) {
                res += end[tmp];
                end[tmp] = 0; //不重复，若可重复此处不置0即可
                tmp = fail[tmp];
            }
        }
        return res;
    }
    void debug() {
        for (int i = 0; i < L; ++i) {
            printf("%d, %d, %d, [%d", i, fail[i], end[i], nxt[i][0]);
            for (int j = 1; j < MAXD; ++j) {
                printf(" %d", nxt[i][j]);
            }
            puts("]");
        }
    }
} ac;

const int MAXL = 64;
char str[MAXL];
char buf[MAX << 1];

int main() {
    int T;
    scanf(" %d", &T);
    while (T--) {
        int n;
        scanf(" %d", &n);
        ac.clear();
        for (int i = 0; i < n; ++i) {
            scanf(" %s", str);
            ac.insert(str);
        }
        ac.build();

        scanf(" %s", buf);
        printf("%d\n", ac.query(buf));
    }
    return 0;
}

几个简单的小题目

• hdu2222，First attempt

/* **********************************************

  File Name: ac_automata.cpp => hdu2222

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月14日 星期五 08时41分23秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
const double EPS = 1e-8;
const double PI = acos(-1.0);

const int MAX = 500007;
const int MAXD = 26; //26 alphas
struct Trie {
    /* 
     * nxt & end is used in trie
     * fail is for ac automata
     */
    int nxt[MAX][MAXD], fail[MAX], end[MAX];
    int root, L; //root node, length(the nodes has been malloc)[0, L]
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L++] = 0;
        return L - 1;
    }
    void clear() {
        L = 0;
        root = newnode();
    }
    void insert(char* buf) {
        int len = strlen(buf);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][buf[i] - 'a'] == -1) {
                nxt[now][buf[i] - 'a'] = newnode();
            }
            now = nxt[now][buf[i] - 'a'];
        }
        ++end[now];
    }
    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    int query(char* buf, int len = -1) {
        if (len == -1) {
            len = strlen(buf);
        }
        int now = root;
        int res = 0;
        for (int i = 0; i < len; ++i) {
            now = nxt[now][buf[i] - 'a'];
            int tmp = now;
            while (tmp != root) {
                res += end[tmp];
                end[tmp] = 0; //不重复，若可重复此处不置0即可
                tmp = fail[tmp];
            }
        }
        return res;
    }
    void debug() {
        for (int i = 0; i < L; ++i) {
            printf("%d, %d, %d, [%d", i, fail[i], end[i], nxt[i][0]);
            for (int j = 1; j < MAXD; ++j) {
                printf(" %d", nxt[i][j]);
            }
            puts("]");
        }
    }
} ac;

const int MAXL = 64;
char str[MAXL];
char buf[MAX << 1];

int main() {
    int T;
    scanf(" %d", &T);
    while (T--) {
        int n;
        scanf(" %d", &n);
        ac.clear();
        for (int i = 0; i < n; ++i) {
            scanf(" %s", str);
            ac.insert(str);
        }
        ac.build();

        scanf(" %s", buf);
        printf("%d\n", ac.query(buf));
    }
    return 0;
}

• hdu2896
• 病毒保证不同，简单统计，随便搞

/* **********************************************

  File Name: 2896.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月14日 星期五 11时25分51秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
const double EPS = 1e-8;
const double PI = acos(-1.0);
const int MAX = 100007;
const int MAXD = 128;
struct Trie {
    int nxt[MAX][MAXD], fail[MAX], end[MAX];
    int root, L;

    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L++] = -1;
        return L - 1;
    }

    void clear() {
        L = 0;
        root = newnode();
    }

    void insert(char* buf, int _end) {
        int len = strlen(buf);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][(int)buf[i]] == -1) {
                nxt[now][(int)buf[i]] = newnode();
            }
            now = nxt[now][(int)buf[i]];
        }
        end[now] = _end;
    }

    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    set<int> query(char* buf) {
        int len = strlen(buf);
        int now = root;
        set<int> res;
        for (int i = 0; i < len; ++i) {
            now = nxt[now][(int)buf[i]];
            int tmp = now;
            while (tmp != root) {
                if (~end[tmp]) {
                    res.insert(end[tmp]);
                }
                tmp = fail[tmp];
            }
        }
        return res;
    }
} ac;
char buf[MAX];

int main() {
    int n, m;
    while (~scanf(" %d", &n)) {
        ac.clear();
        for (int i = 1; i <= n; ++i) {
            scanf(" %s", buf);
            ac.insert(buf, i);
        }
        ac.build();
        scanf(" %d", &m);
        int sum = 0;
        for (int i = 1; i <= m; ++i) {
            scanf(" %s", buf);
            auto v = ac.query(buf);
            if (!v.empty()) {
                ++sum;
                printf("web %d:", i);
                for (auto it = v.begin(); it != v.end(); ++it) {
                    printf(" %d", *it);
                }
                puts("");
            }
        }
        printf("total: %d\n", sum);
    }
    return 0;
}

• hdu3065
• 要打印匹配串：打标记，Trie上节点打前驱和字符标记。P.S.空间上还可以优化

/* **********************************************

  File Name: 3065.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月14日 星期五 11时46分10秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
const double EPS = 1e-8;
const double PI = acos(-1.0);

const int MAX = 50007;
const int MAXD = 128; //26 alphas
struct Trie {
    /* 
     * nxt & end is used in trie
     * fail is for ac automata
     */
    int nxt[MAX][MAXD], fail[MAX], end[MAX], pre[MAX];
    char dad[MAX];
    int root, L; //root node, length(the nodes has been malloc)[0, L]
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        pre[L] = -1;
        end[L++] = 0;
        return L - 1;
    }
    void clear() {
        L = 0;
        root = newnode();
    }
    void insert(char* buf) {
        int len = strlen(buf);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][(int)buf[i]] == -1) {
                nxt[now][(int)buf[i]] = newnode();
                pre[nxt[now][(int)buf[i]]] = now;
                dad[nxt[now][(int)buf[i]]] = buf[i];
            }
            now = nxt[now][(int)buf[i]];
        }
        ++end[now];
    }

    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    map<int, int> query(char* buf, int len = -1) {
        if (len == -1) {
            len = strlen(buf);
        }
        int now = root;
        map<int, int> res;
        for (int i = 0; i < len; ++i) {
            now = nxt[now][(int)buf[i]];
            int tmp = now;
            while (tmp != root) {
                if (end[tmp] > 0) {
                    ++res[tmp];
                }
                tmp = fail[tmp];
            }
        }
        return res;
    }
    void debug() {
        for (int i = 0; i < L; ++i) {
            printf("%d, %d, %d, [%d", i, fail[i], end[i], nxt[i][0]);
            for (int j = 1; j < MAXD; ++j) {
                printf(" %d", nxt[i][j]);
            }
            puts("]");
        }
    }
} ac;

const int MAXL = 64;
char str[MAXL];
char buffer[MAX * 40];

int main() {
    int n;
    while (~scanf(" %d", &n)) {
        ac.clear();
        for (int i = 1; i <= n; ++i) {
            scanf(" %s", str);
            ac.insert(str);
        }
        ac.build();
        scanf(" %s", buffer);
        auto mp = ac.query(buffer);
        for (auto it = mp.begin(); it != mp.end(); ++it) {
            int now = it->first;
            int idx = MAXL - 1;
            str[idx--] = '\0';
            while (now != ac.root) {
                str[idx--] = ac.dad[now];
                now = ac.pre[now];
            }
            ++idx;
            printf("%s: %d\n", str + idx, it->second);
        }
    }
    return 0;
}

• zoj3430
• 解码一下即可。debug了好久，最后发现Base64直接解码出来的字符可能不是$ASCII$码，就如$1111\ 1111$对应到$ASCII$后是$EOF\dots$真让人难堪。。。所以字符集开到256就可以过了…一部分调试中间修改导致整个代码看起来丑陋了一些，不愿改了。。

/* **********************************************

  File Name: 3430.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月14日 星期五 13时28分38秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
const double EPS = 1e-8;
const double PI = acos(-1.0);
const int MAX = 50007;
const int MAXD = 256;

/*
 * Base64 Decode
 */
static const char cb64[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
bool pool[50007];
inline int dic64(char& c) {
    if (isupper(c)) {
        return c - 'A';
    } else if (islower(c)) {
        return c - 'a' + 26;
    } else if (isdigit(c)) {
        return c - '0' + 52;
    } else {
        return c == '+' ? 62 : 63;
    }
}
void decode64(char source[], int dest[]) {
    int len = strlen(source);
    int bit = len * 6;
    memset(pool, false, sizeof(bool) * bit);
    while (source[len - 1] == '=') {
        --len;
        bit -= 8;
    }
    //printf("bit = %d\n", bit);
    for (int i = 0, j = 0; i < len; ++i, j += 6) {
        int c = dic64(source[i]);
        for (int k = j + 5; k >= j; --k) {
            pool[k] = c & 1;
            c >>= 1;
        }
    }
    int p = 0;
    for (int i = 0; i < bit; i += 8) {
        dest[p] = 0;
        for (int j = 0; j < 8; ++j) {
            dest[p] <<= 1;
            if (pool[i + j]) {
                ++dest[p];
                //dest[p] = (char)((int)dest[p] + 1);
            }
        }
        ++p;
    }
    dest[p] = -1;
}
/**********************************************/

struct Trie {
    /* 
     * nxt & end is used in trie
     * fail is for ac automata
     */
    int nxt[MAX][MAXD], fail[MAX], end[MAX];
    int root, L; //root node, length(the nodes has been malloc)[0, L]
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L++] = 0;
        return L - 1;
    }
    void clear() {
        L = 0;
        root = newnode();
    }
    void insert(int* buf, int _id) {
        int* p = buf;
        int now = root;
        while (~(*p)) {
            if (nxt[now][*p] == -1) {
                nxt[now][*p] = newnode();
            }
            now = nxt[now][*p++];
        }
        end[now] = _id;
    }
    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    set<int> query(int* buf) {
        int* p = buf;
        int now = root;
        set<int> res;
        while (~(*p)) {
            now = nxt[now][*p++];
            int tmp = now;
            while (tmp != root) {
                if (end[tmp]) {
                    res.insert(end[tmp]);
                }
                tmp = fail[tmp];
            }
        }
        return res;
    }
    void debug() {
        for (int i = 0; i < L; ++i) {
            printf("%d, %d, %d, [%d", i, fail[i], end[i], nxt[i][0]);
            for (int j = 1; j < MAXD; ++j) {
                printf(" %d", nxt[i][j]);
            }
            puts("]");
        }
    }
} ac;

const int MAXL = 128;
char str[MAXL];
char buf[MAX];
int jj[MAX];

int main() {
    /*
    while (cin >> buf) {
        decode64(buf, buf);
        cout << buf << endl;
    }
    return 0;
    */

    int n;
    while (~scanf(" %d", &n)) {
        ac.clear();
        for (int i = 1; i <= n; ++i) {
            scanf(" %s", str);
            decode64(str, jj);
            ac.insert(jj, i);
        }
        ac.build();

        int m;
        scanf(" %d", &m);
        while (m--) {
            scanf(" %s", buf);
            decode64(buf, jj);
            printf("%d\n", (int)ac.query(jj).size());
        }
        puts("");
    }
    return 0;
}

• poj2778 DNA Sequence
• 给几个$DNA$串，问长度为$L$的串中，不包含上述基因的有多少种。
• 构造矩阵$A$，$A_{ij}$表示从自动机的状态$i$经过$1$步到达状态$j$的方案数。我们考虑到，为了满足“不包含给定字符串”这个条件，那么到达的状态$j$不应该是一个接受状态。于是，在建立自动机时，我们将所有状态分两类，第一类是所谓合法的状态，从起始状态经过任意步到达，均不会匹配上任一个给定串；第二类是所谓非法状态，这些状态包含了匹配内容。
• 我们只需要标记出第二类状态即可。首先，所有的接受状态都属于第二类，另外，通过自身$fail$指针可以连接到一个第二类状态的状态，也应该属于第二类状态。
• 标记完成后，构造矩阵只需要遍历所有$L'$个状态即可（$L'$是自动机的总状态数）。
• 考虑上述关系矩阵，我们发现，如果要求长度$L=1$，则就是第一行的和；再考虑平方$B=A^2$，显然 $$B_{ij}=\sum{A_{ik}*A_{kj}}$$ 表示的是状态$i$经过$2$步到达状态$j$的方法数，即途径$1$个状态$k$到达$j$。以此类推，$A^L$第一行的和就表示初始状态经$L$步能到达合法状态的所有方法数目，此即答案。

/* **********************************************

  File Name: 2778.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月15日 星期六 11时04分14秒

*********************************************** */
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cmath>
#include <utility>
#include <cassert>
#include <iostream>
using namespace std;

typedef pair<int, int> P;
typedef long long ll;
const double EPS = 1e-8;
const double PI = acos(-1.0);

const int MOD = 100000;
const int MAX = 107;
const int MAXD = 4;
//static const char tle[] = "ATCG";
//struct Mat;
struct Mat {
    int sz;
    ll a[MAX][MAX];

    Mat(int _sz = 1, bool flag = false): sz(_sz) {
        memset(a, 0, sizeof(a));
        if (flag) {
            for (int i = 0; i < sz; ++i) {
                a[i][i] = 1;
            }
        }
    }
    Mat operator*(const Mat& b)const {
        Mat ret(sz);
        for (int i = 0; i < sz; ++i) {
            for (int j = 0; j < sz; ++j) {
                for (int k = 0; k < sz; ++k) {
                    ret.a[i][j] += a[i][k] * b.a[k][j];
                    if (ret.a[i][j] > MOD) {
                        ret.a[i][j] %= MOD;
                    }
                }
            }
        }
        return ret;
    }
};
Mat operator^(Mat& a, int nn) {
    Mat res(a.sz, true);
    int n = nn;
    while (n) {
        if (n & 1) {
            res = res * a;
        }
        a = a * a;
        n >>= 1;
    }
    return res;
}

struct Trie {
    /* 
     * nxt & end is used in trie
     * fail is for ac automata
     */
    int nxt[MAX][MAXD], fail[MAX];
    bool end[MAX];
    int root, L; //root node, length(the nodes has been malloc)[0, L]
    int operator^(const char& c) {
        switch(c) {
            case 'A': return 0;
            case 'C': return 1;
            case 'G': return 2;
            case 'T': return 3;
            default: return 0;
        }
    }
    int getch(char ch) {
        switch(ch) {
            case 'A': return 0;
            case 'C': return 1;
            case 'G': return 2;
            default: return 3;
        }
    }
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L++] = false;
        return L - 1;
    }
    void clear() {
        L = 0;
        root = newnode();
    }
    void insert(char* buf) {
        int len = strlen(buf);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][getch(buf[i])] == -1) {
                nxt[now][getch(buf[i])] = newnode();
            }
            now = nxt[now][getch(buf[i])];
            /*
            if (nxt[now][(*this) ^ buf[i]] == -1) {
                nxt[now][(*this) ^ buf[i]] = newnode();
            }
            now = nxt[now][(*this) ^ buf[i]];
            */
        }
        end[now] = true;
        //++end[now];
    }
    void build() {
        queue<int> Q;
        //fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }

        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            if (end[fail[now]]) {
                end[now] = true;
            }
            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    int gao1gao(int n) {
        Mat res(L);
        for (int i = 0; i < L; ++i) {
            for (int j = 0; j < MAXD; ++j) {
                if (!end[nxt[i][j]]) {
                    ++res.a[i][nxt[i][j]];
                }
            }
        }
        for (int i = 0; i < L; ++i) {
            for (int j = 0; j < L; ++j) {
                printf("%2lld ", res.a[i][j]);
            }
            puts("");
        }
        res = res ^ n;
        int sum = 0;
        for (int i = 0; i < L; ++i) {
            sum += res.a[0][i];
            if (sum >= MOD) {
                sum %= MOD;
            }
        }
        return sum;
    }
} ac;
char str[MAX];

int main() {
    int m, n;
    while (cin >> m >> n) {
        ac.clear();
        for (int i = 0; i < m; ++i) {
            cin >> str;
            ac.insert(str);
        }
        ac.build();
        cout << ac.gao1gao(n) << endl;
    }
    return 0;
}

• hdu2243
• 和上述类似，求出长度$L$以内不合法的，再用总数减去即可。为啥不能直接从正面求捏？考虑上面对关系矩阵的幂的分析过程即可。显然我们需要求得
  $$\sum_{i=1}^{L}{\begin{vmatrix} A \\ \end{vmatrix}^i}$$ 于是构造矩阵
  $$\begin{vmatrix} A&E\\ 0&E\\ \end{vmatrix}$$ 其中$E$表示单位矩阵。求出该矩阵的$L+1$次方，则右上角的分块矩阵即是我们要求的和
• 另外，由于上面构造了一个需要求$L+1$次方的矩阵，不能保证$L+1$在$int$范围内，需要$long\ long$或者先算$L$次再额外算一次。
• 求出 $$B=\sum_{i=1}^{L}{\begin{vmatrix} A \\ \end{vmatrix}^i}$$ 后(下标都从0开始算), $$ans=\sum_{i=1}^{L}{26^i}-\sum_{i=L}^{2L-1}B_{0i}$$
  
  • $P.S.$ $\sum_{i=1}^{L}26^i$部分同样可以构造一个矩阵
    $$\begin{vmatrix} 26&1 \\ 0&1 \\ \end{vmatrix}$$ 通过其$L+1$次方求得，同样地，自己推一推就好了。

/* **********************************************

  File Name: 2243.cpp

  Auther: zhengdongjian@tju.edu.cn

  Created Time: 2015年08月16日 星期日 13时43分01秒

*********************************************** */
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> P;
typedef long long ll;
typedef unsigned long long ull;
const double EPS = 1e-8;
const double PI = acos(-1.0);

const int MAX = 64;
const int MAXD = 26;
struct Mat {
    int sz;
    ull a[MAX][MAX];
    Mat(int _sz = MAX, bool flag = false): sz(_sz) {
        memset(a, 0, sizeof(a));
        if (flag) {
            for (int i = 0; i < sz; ++i) {
                a[i][i] = 1;
            }
        }
    }
    Mat operator*(const Mat& b)const {
        Mat res(sz);
        for (int i = 0; i < sz; ++i) {
            for (int j = 0; j < sz; ++j) {
                for (int k = 0; k < sz; ++k) {
                    res.a[i][j] += a[i][k] * b.a[k][j];
                }
            }
        }
        return res;
    }
    Mat operator^(ll n)const {
        Mat a(*this);
        Mat res(sz, true);
        while (n) {
            if (n & 1) {
                res = res * a;
            }
            a = a * a;
            n >>= 1;
        }
        return res;
    }
};
struct Trie {
    int root, L;
    int nxt[MAX][MAXD], fail[MAX];
    int end[MAX];
    void clear() {
        L = 0;
        root = newnode();
    }
    int newnode() {
        memset(nxt[L], -1, sizeof(int) * MAXD);
        end[L] = false;
        return L++;
    }
    void insert(const char* s) {
        int len = strlen(s);
        int now = root;
        for (int i = 0; i < len; ++i) {
            if (nxt[now][s[i] - 'a'] == -1) {
                nxt[now][s[i] - 'a'] = newnode();
            }
            now = nxt[now][s[i] - 'a'];
        }
        end[now] = true;
    }
    void build() {
        queue<int> Q;
        fail[root] = root;
        for (int i = 0; i < MAXD; ++i) {
            if (nxt[root][i] == -1) {
                nxt[root][i] = root;
            } else {
                fail[nxt[root][i]] = root;
                Q.push(nxt[root][i]);
            }
        }
        while (!Q.empty()) {
            int now = Q.front();
            Q.pop();

            if (end[fail[now]]) {
                end[now] = true;
            }
            for (int i = 0; i < MAXD; ++i) {
                if (nxt[now][i] == -1) {
                    nxt[now][i] = nxt[fail[now]][i];
                } else {
                    fail[nxt[now][i]] = nxt[fail[now]][i];
                    Q.push(nxt[now][i]);
                }
            }
        }
    }
    ull gao1gao(ll l) {
        Mat res(L * 2);
        for (int i = 0; i < L; ++i) {
            for (int j = 0; j < MAXD; ++j) {
                if (!end[nxt[i][j]]) {
                    ++res.a[i][nxt[i][j]];
                }
            }
        }
        for (int i = L; i < 2 * L; ++i) {
            res.a[i][i] = 1;
            res.a[i - L][i] = 1;
        }
        /*
        cout << "------------" << endl;
        for (int i = 0; i < 2 * L; ++i) {
            for (int j = 0; j < 2 * L; ++j) {
                printf("%2llu ", res.a[i][j]);
                //cout << res.a[i][j] << ' ';
            }
            cout << endl;
        }
        Mat res1 = res ^ l;
        ull sum1 = 0ULL;
        for (int i = 0; i < L; ++i) {
            sum1 += res1.a[0][i];
        }
        return sum1;
        */
        res = res ^ (l + 1);

        Mat tp(2);
        tp.a[0][0] = 26, tp.a[0][1] = tp.a[1][1] = 1;
        tp = tp ^ (l + 1);

        ull sum = tp.a[0][1];
        for (int i = L; i < 2 * L; ++i) {
            sum -= res.a[0][i];
        }
        return sum;
    }
} o_o;

int main() {
    int n;
    ll l;
    while (cin >> n >> l) {
        char str[MAX];
        o_o.clear();
        for (int i = 0; i < n; ++i) {
            cin >> str;
            o_o.insert(str);
        }
        o_o.build();

        cout << o_o.gao1gao(l) << endl;
    }
    return 0;
}