【笔试强训day15】

目录

第一题：平方数

输入描述:

输出描述:

输入

输出

第二题：分组 

题目描述

输入描述:

输出描述:

输入

输出

第三题：拓扑排序

描述

输入描述：

输出描述：

输入：

输出：

---

第一题：平方数

题目链接：登录—专业IT笔试面试备考平台_牛客网

牛妹是一个喜欢完全平方数的女孩子。
牛妹每次看到一个数 x，都想求出离 x 最近的完全平方数 y。
每次手算太麻烦，所以牛妹希望你能写个程序帮她解决这个问题。
形式化地讲，你需要求出一个正整数 y，满足 y 可以表示成 a2a^2a2（a 是正整数），使得 |x-y| 的值最小。可以证明这样的 y 是唯一的。

输入描述:

一行，一个整数 x (1≤x≤10^12)，表示牛妹询问的数。

输出描述:

一行，一个整数 y，表示离 x 最近的完全平方数 y。

示例1

输入

5

输出

4

对输入的数进行开方，然后将开方结果强转为整数，设为n，最后判断输入的x是离n^2近一些还是离（n + 1）^ 2近一些即可。比如输入的数为5，开方然后转为整数后是2,2的平方为4,2 + 1的平方为9，显然5离4更近一些。注意数据范围，整形int会溢出。

#include <iostream>
#include <cmath>
using namespace std;

typedef long long LL;

int main()
{
    LL x;
    cin >> x;
    LL n = sqrt(x);
    LL left = n * n, right = (n + 1) * (n + 1);
    if(abs(left - x) < abs(right - x)) cout << left << endl;
    else cout << right << endl;
    return 0;
}

第二题：分组 

题目链接：登录—专业IT笔试面试备考平台_牛客网

题目描述

dd当上了宣传委员，开始组织迎新晚会，已知班里有n个同学，每个同学有且仅有一个擅长的声部，把同学们分成恰好m组，为了不搞砸节目，每一组里的同学都必须擅长同一个声部，当然，不同组同学擅长同一个声部的情况是可以出现的，毕竟一个声部也可以分成好几个part进行表演，但是他不希望出现任何一组的人过多，否则可能会导致场地分配不协调，也就是说，她希望人数最多的小组的人尽可能少，除此之外，对组内人员分配没有其他要求，她希望你告诉她，这个值是多少，如果无法顺利安排，请输出-1

输入描述:

第一行两个数个数n,m(1≤m≤n≤100000)表示人数
接下来一行n个数,a[i](1≤a[i]≤n)表示第i个学生的擅长声部

输出描述:

输出一个数，表示人数最多的小组的人数

示例1

输入

5 3

2 2 3 3 3

输出

2

题目的意思是：n个人，分为m组，每组都是擅长同一个声部的同学，不同组之间可以擅长相同的声部，输出人数最多小组的最小值。

以上面例子为例：五人分三组。

 

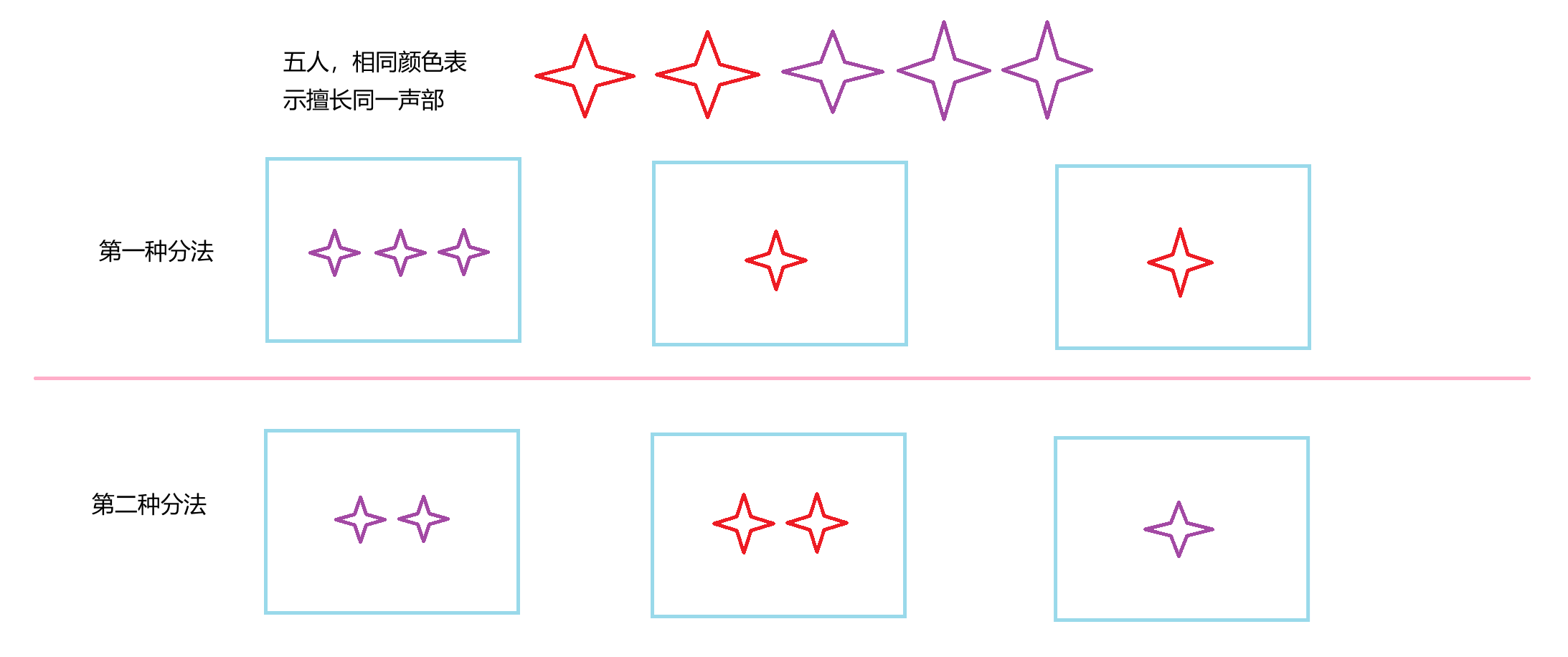
第一中分法中人数最多的组有3人，第二种分法中人数最多的有2人，所以输出2. 

        一开始可能考虑的是把擅长同一声部的同学分为多少组，一共分m组，通过以上的枚举来得到答案。但这样子很麻烦，因为擅长同一声部的同学分组的情况比较多，不好枚举。这一种思想就是通过枚举分组情况来得到答案。

        另一种思想就是正难则反——枚举答案，这题正好可以根据二段性来做优化，即二分答案。曾经写力扣周赛时也碰到了要二分答案的题目，不过具体是什么题目忘记啦。答案至少为1（一个组至少有一个人吧），所以就从1开始枚举答案。

        问题是，枚举到哪，也就是枚举的上限是多少？枚举到擅长某一声部的最大人数。比如擅长2号声部的同学最多，有k人。在前面例子中，人数最多也就是把2号声部的同学全放一组，一共k人。所以从1枚举到k即可。如果有答案的话一定在1到k之间。

        那么同一个声部的同学要分为多少组呢？k / ans + (k % ans == 0 ? 0 : 1)。ans表示答案，即一组的最多人数。如果k不能整除，那么在多开一组来存放。

        问题来了，一共分多少组才是合法的呢？所有声部经过上面公式的分法，如果分出的组数小于等于m组即是合法的。因为如果分出的组数小于m组的话，可以继续拆分出来凑够m组，但是不会改变ans，即不会使得最多人数的那一组人数变少，进而ans减小。因为我们是从小到大枚举ans的。枚举到当前ans时，说明前面较小的ans都不满足要求（虽然ans较小但是组数太多，超过了m组）。

        最后，就是不能顺利安排的情况。如果擅长声部的种类大于m，那么就不能安排。比如有擅长 2 3 4声部的同学，然后要求是分为2组，那么是无论如何都做不到同一个组里擅长的都是同一声部的。

 

/***
****暴力枚举答案和二分答案都可以
***/
#include <iostream>
#include <unordered_map>
using namespace std;

unordered_map<int, int> map;//存储学生擅长声部的信息<声部，人数>
int n, m;
int maxLimit;//枚举的最大上限

//判断最多人数为ans时，能否分成m组
bool check(int ans)
{
    int flag = 0;
    for(auto& [a, b] : map)
    {
        int tmp = b / ans + (b % ans == 0 ? 0 : 1);
        flag += tmp;
    }
    return flag <= m;//如果满足就是合法的分组
}
int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        maxLimit = max(maxLimit, ++map[x]);
    }
    int kinds = map.size();//声部的种类
    if(kinds > m)
    {
        cout << -1 << endl;
    }
    else
    {
        //暴力枚举
        /*
        for(int ans = 1; ans <= maxLimit; ans++)
        {
            if(check(ans))
            {
                cout << ans << endl;
                break;
            }
        }
        */
        //二分答案
        int left = 0, right = maxLimit;
        while(left < right)
        {
            int mid = (left + right) / 2;
            if(!check(mid))//mid偏小了，分的组多于m，即枚举的答案偏小了
                left = mid + 1;
            else
                right = mid;
        }
        cout << left << endl;
    }
    return 0;
}

第三题：拓扑排序

题目链接：【模板】拓扑排序_牛客题霸_牛客网

描述

给定一个包含n个点m条边的有向无环图，求出该图的拓扑序。若图的拓扑序不唯一，输出任意合法的拓扑序即可。若该图不能拓扑排序，输出−1。

输入描述：

第一行输入两个整数n,m ( 1≤𝑛,𝑚≤2⋅10^5)，表示点的个数和边的条数。
接下来的𝑚m行，每行输入两个整数𝑢𝑖,𝑣𝑖ui​,vi​ (1≤𝑢,𝑣≤𝑛1≤u,v≤n)，表示𝑢𝑖ui​到𝑣𝑖vi​之间有一条有向边。

输出描述：

若图存在拓扑序，输出一行𝑛n个整数，表示拓扑序。否则输出−1−1。
注意：输出的最后一个数后面不要带空格。

示例1

输入：

5 4
1 2
2 3
3 4
4 5

输出：

1 2 3 4 5

这是一道拓扑排序的模板题，直接按固定步骤来就可以了。

拓扑排序解题步骤：                                                                                                                  1）建图（存放边）。

2）把所有入度为0的点加入队列中。

3）当队列不为空时：

①   拿出队头元素，并将该元素存入保存结果的数组中。

②   修改拿出的队头元素指向的点的入度。

③   在修改入度后，如果碰到入度减为0的点，则加入队列中。       

4）判断是否存在拓扑序，如果结果数组中的元素个数和总的点数n相等，那么就有拓扑序，        反之没有。                                   

 

/****
*****题目有很隐蔽的坑，也许因为这个原因才导致通过率很低
*/
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

const int N = 2e5 + 10;
vector<vector<int>> edges(N);//存放图（边）
vector<int> ret;//存放结果的数组
int in[N];//统计入度

int main() 
{
    int n, m;
    cin >> n >> m;
    //1.建图（存放边）
    while(m--)
    {
        int a, b;
        cin >> a >> b;
        edges[a].push_back(b);//存放边
        in[b]++;//更新入度
    }
    //2.把所有入度为0的点加入队列中
    queue<int> q;
    for(int i = 1; i <= n; i++)
    {
        if(in[i] == 0)
            q.push(i);
    }
    //3.当队列不为空时，循环操作
    while(!q.empty())
    {
        //拿出队头元素，并将该元素存入保存结果的数组中
        int val = q.front();
        q.pop();
        ret.push_back(val);
        //修改拿出的队头元素指向的点的入度
        //在修改入度后，如果碰到入度减为0的点，则加入队列中
        for(auto num : edges[val])
        {
            if(--in[num] == 0)
                q.push(num);
        }
    }
    //4.判断是否存在拓扑序
    if(ret.size() != n)
    {
        cout << -1 << endl;
    }
    else 
    {
        // for(int i = 0; i < n; i++)
        // {
        //     cout << ret[i] << " ";//有坑，最后一个元素输出时，还带了一个空格，所以错误
        // }
        // cout << endl;
        for(int i = 0; i < n - 1; i++)
        {
            cout << ret[i] << " ";
        }
        cout << ret[n - 1] << endl;
    }
    return 0;
}