一个博弈游戏，据说智商130才看的懂

博弈论是一门非常有意思的学问，之前小灰曾经分享过两个著名的博弈场景：囚徒困境和智猪博弈。

今天，我们来介绍一个更加烧脑的博弈游戏：硬币游戏。

游戏规则

小灰和大黄都有若干块糖果。有一天大黄提议和小灰玩一个游戏。这是个什么游戏呢？规则很简单：

首先，他们各自拿出一枚硬币，并同时亮出

• 如果同为正面，大黄给小灰3块糖果

• 如果同为反面，大黄给小灰1块糖果

  

• 如果是一正一反，小灰给大黄2块糖果

  

  

经过若干轮游戏，小灰的糖果都被大黄赢走了......

概率里的陷阱

为什么会发生这样的事情呢？我们可以好好探究一下这个问题。让我们试试看用一个表格表示小灰的收入：

↓ 小灰的选择 → 大黄的选择	亮正面	亮反面
亮正面	3	-2
亮反面	-2	1

乍一看每种情况出现的概率都是 ，因此这个游戏似乎是极其公平的？那么是因为小灰运气不好呢？不不不，这个游戏里，其实包含着一个隐蔽 的漏洞：

如果是随机的抛硬币，那么每种情况出现的概率的确是 ，但是不要忘了，这个游戏的规则不是随机的抛硬币，我们可以主观选择自己亮出的硬币是正面还是反面，就像在玩“石头剪子布”一样。

我们假设大黄出正面的概率为p，小灰出正面的概率为  ，那么我们可以得到下图：

左图表示大黄，右图表示小灰

可以看到，此时 表示大黄出正面的概率， 表示大黄出反面的概率， 表示小灰出正面的概率，而 表示小灰出反面的概率。

以此为基础，很容易计算出：

• 两人同时出正面的概率是 pq , 小灰的收获是3

• 两人同时出反面时的概率是(1-p)(1-q) , 小灰的收获是1

• 小灰出正面，大黄出反面的概率是(1-p)q , 小灰的收获是-2

• 小灰出反面，大黄出正面的概率是p(1-q) , 小灰的收获是-2

我们用一个字母 表示小灰的预期收获，那么 的值为：

（也就是把他们加在一起了）

简化之得：

下面的分析会比较烧脑，涉及到含参数不等式以及减函数的知识，一次看不明白的小伙伴可以多看几遍。

求解方程

大黄想要赢小灰，就要使小灰的收入 小于 ，我们可以列出不等式：

把 的值代入，即：

大黄无法修改小灰的 值，但是他却能修改自己的 值，因此我们要求的就是 值的解集。把原式当做一个未知数为  的含参数不等式，先将参数项移至右面，把未知数项放在左面

合并同类项可得到：

对于一个含参数的不等式，我们要进行分类讨论：

• 当参数>0时（两边同时除以参数，不等式符号不变）

• 当参数<0时（两边同时除以参数，不等式符号改变）

• 当参数=0时（原式有任意解）

  上面所说的参数，是指 8q-3 这一项

注：由于 在这里表示一个概率，因此 的取值范围一定只有 ，也就是说，当 为任意解时， 也仅仅只对任意的 成立。

对于上面参数不等式的三种情况，让我们分别进行具体讨论：

情况A，当参数大于0，即 时：

（不等式符号不变）

当定义域为 时，有函数

对应的函数图像为

将其不断放大，直到 的定义域为 ，发现函数图像的曲线是向下的：

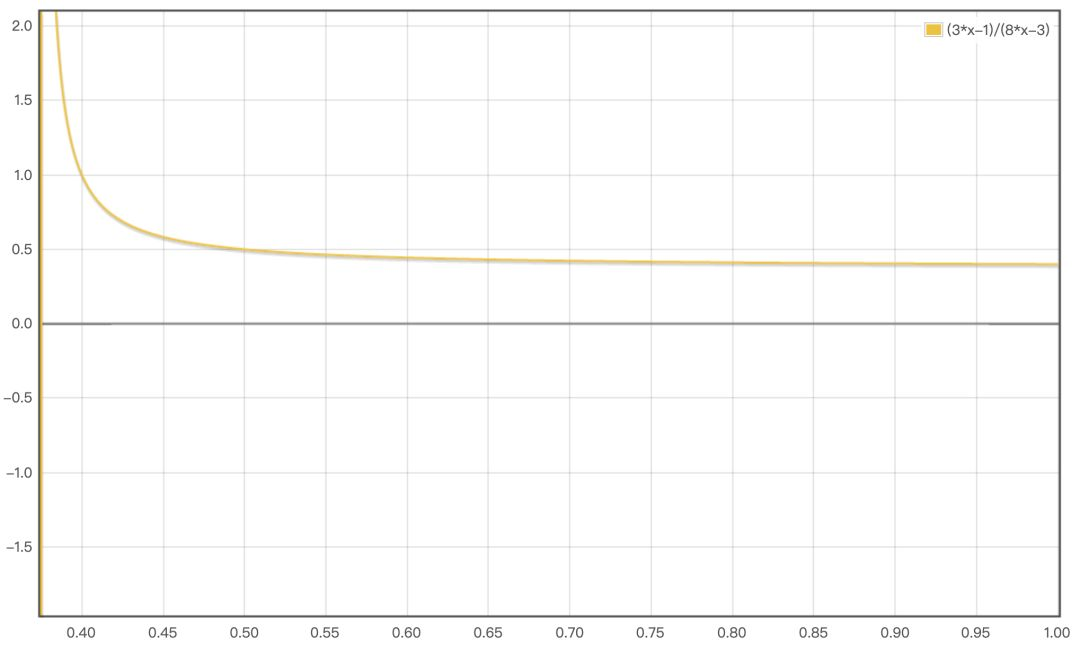
也就是说，这是一个减函数，其定义域上的任何自变量 都有对应的 。

为了保证（在q的定义域内）不等式成立，p必须小于f(1)，也就是 时，原式成立。

情况B，当参数小于0，即 时：

（不等式符号相反）

当定义域为 时，函数 为一个减函数，具体的函数图像可以看下图：

虽然它的曲线和刚才略有不同，不过仍然符合减函数的定义。

为了保证在（q的定义域内）不等式成立，p必须大于f(0)，也就是 时，原式成立。

情况C，当参数等于0，即 时：

（任意解）

（仍然符合 ）

我们把情况A、情况B、情况C当中p的取值范围求一个交集，最终得出：当大黄把亮正面的概率 控制在 时，小灰一定会输。

应用场景

这个游戏远远不止于此，其实它还能应用到生活中的很多场景里。我们以炒股为例子，把大黄想象成庄家，把亮正面想成做空，亮反面想成做多，那么在这个由庄家掌握的局面下，很显然投资者（也就是小灰）一定是会吃亏的。因此，请远离炒股，炒股有风险，投资需谨慎。

这个博弈论的问题就讲解到这里，谢谢阅读！

投稿作者：王乙堃

编辑整理：小灰

需要特别说的的是，王乙堃同学年仅12岁，在读小学六年级，能写出这样的文章真的很了不起，非常感谢他的投稿！

—————END—————

喜欢本文的朋友，欢迎关注公众号 程序员小灰，收看更多精彩内容

欢迎长按二维码关注 小灰学英语，你所学到的不只是英语！

给个[在看]，是对小灰最大的支持！