Wall--凸包

Wall

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 35059		Accepted: 11945

Description

Once upon a time there was a greedy King who ordered his chief Architect to build a wall around the King's castle. The King was so greedy, that he would not listen to his Architect's proposals to build a beautiful brick wall with a perfect shape and nice tall towers. Instead, he ordered to build the wall around the whole castle using the least amount of stone and labor, but demanded that the wall should not come closer to the castle than a certain distance. If the King finds that the Architect has used more resources to build the wall than it was absolutely necessary to satisfy those requirements, then the Architect will loose his head. Moreover, he demanded Architect to introduce at once a plan of the wall listing the exact amount of resources that are needed to build the wall. 

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King's requirements. 

The task is somewhat simplified by the fact, that the King's castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle's vertices in feet.

Input

The first line of the input file contains two integer numbers N and L separated by a space. N (3 <= N <= 1000) is the number of vertices in the King's castle, and L (1 <= L <= 1000) is the minimal number of feet that King allows for the wall to come close to the castle. 

Next N lines describe coordinates of castle's vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.

Output

Write to the output file the single number that represents the minimal possible length of the wall in feet that could be built around the castle to satisfy King's requirements. You must present the integer number of feet to the King, because the floating numbers are not invented yet. However, you must round the result in such a way, that it is accurate to 8 inches (1 foot is equal to 12 inches), since the King will not tolerate larger error in the estimates.

Sample Input

9 100
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200

Sample Output

1628

Hint

结果四舍五入就可以了

题目链接：http://poj.org/problem?id=1113

算是我的凸包的巩固题吧，一上午卡了两个凸包题，幸亏子祥大大不远千山万里走了1分钟的路程来给我找bug，万分感谢+_+|||

题目的意思是说：给定多边形城堡的n个顶点，绕城堡外面建一个围墙，围住所有点，并且墙与所有点的距离至少为L，求这个墙最小的长度。

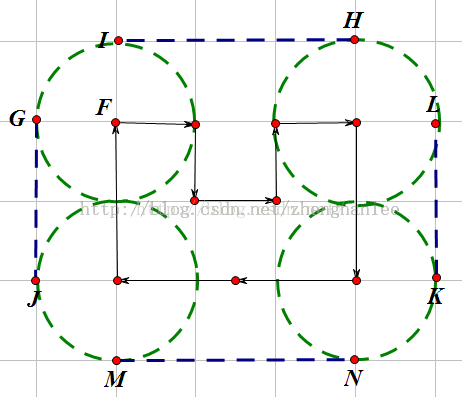
题解用一张图就能说明白，我去找找：

图片转自：http://blog.csdn.net/r1986799047/article/details/48243105

是不是这样就知道怎么做了，一定要注意，题目上画的是凹包，不是凸包，但是求周长的话不影响。

上代码，纯裸敲，大神勿喷，望指点

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
struct node
{
	int x;
	int y;
} point[100000];
int n;
int s[100000], top;//模拟栈
double chacheng(struct node a, struct node b, struct node c)//函数名就是任性
{
	return ((a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x));
}
double dist(struct node a, struct node b)//距离
{
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
bool cmp(struct node a,struct node b)//排序函数的cmp
{
    int k=chacheng(a,b,point[0]);
    if(k>0)
        return 1;
    else if(k==0&&dist(a,point[0])<dist(b,point[0]))
        return 1;
    else
        return 0;

}
double Grahamscan()//Grahamscan扫描法
{
	int k = 0;
	int i;
	for (i = 1; i < n; i++)
	{
		if (point[i].x < point[k].x || (point[i].x == point[k].x && point[i].y < point[k].y))
		{
			k = i;
		}
	}
	swap(point[0], point[k]);
	sort(point,point+n,cmp);
	for (i = 0; i <= 2; i++)
	{
		s[i] = i;
	}
	top = 2;//前3个元素进栈
	for (i = 3; i < n; i++)
	{
		while (chacheng(point[i], point[s[top]], point[s[top - 1]])>=0)
		{
		    top--;
			if (top == 0)
			{
				break;
			}

		}
		top++;
		s[top] = i;
	}
	double sum = 0;
	for (i = 0; i < top; i++)//凸包的周长
	{
		sum += dist(point[s[i]], point[s[i + 1]]);
	}
	sum += dist(point[s[0]], point[s[top]]);//加上最后一个点到第一个点的距离
	return sum;
}
int main()
{
	int ll;
	while (~scanf("%d%d", &n, &ll))
	{
		int i;
		for (i = 0; i < n; i++)
		{
			scanf("%d%d", &point[i].x, &point[i].y);
		}
		double h = Grahamscan();
		h += 2 * 3.1415926 * ll;//加上一个圆的周长
		printf("%1.f\n", h);
	}
	return 0;
}