使用二叉树解决折纸问题

• 题目：

  请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。此时 折痕是凹下去的，即折 痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2 次，压出折痕后展开，此时有三条折痕，从上 到下依次是下折痕、下折痕和上折痕。 给定一 个输入参数N，代表纸条都从下边向上方连续对折N次，请从上到下打印所有折痕的方向 例如：N=1时，打 印： down；N=2时，打印： down down up

分析:

咱们可以自己试着用值，折一次，两次，三次，观察折出来的折痕，博主自己尝试之后发现情况入下图：

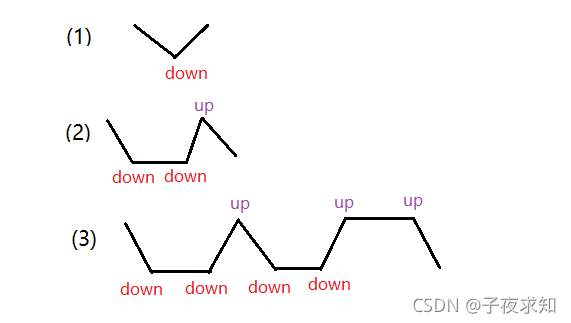
我们可以使用二叉树来解决这道题，根据三次的折痕我们可以发现二叉树有如下规律：

• 根结点为下折痕；
• 每一个结点的左子节点为下折痕；
• 每一个结点的右子节点为上折痕；

由上述规律可以画出如下的二叉树：

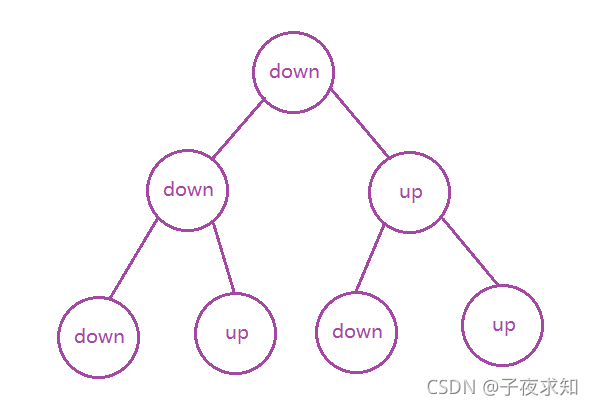
实现步骤

1. 定义结点类
2. 构建深度为N的折痕树；
3. 使用中序遍历，打印出树中所有结点的内容；

代码如下：（代码中的队列数据结构参照上一篇文章）

public class PaperFolding {
    /**
     * 定义结点数据结构
     */
    private static class Node<T>{
        private T key;     // 键
        private T value;   // 值
        private Node left;      // 左孩子
        private Node right;     // 右孩字

        public Node(T key, T value, Node left, Node right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    /**
     * 打印二叉树：使用中序遍历（左根右），打印出二叉树的左右结点
     */
    public static void printTree(Node tree){
        if(tree==null){
            return;
        }
        printTree(tree.left);
        System.out.print(tree.value+" ");
        printTree(tree.right);
    }

    /**
     * 构造折痕树
     * @param time  折叠次数
     * @return
     */
    public static Node createFoldTree(int time){
        Node root= null;
        // 创建深度为 time 的二叉树
        for (int i = 0; i < time; i++){
            if(i == 0){    // 折叠次数为1的时候 直接给根节点赋值"down"
                root = new Node(null,"down",null,null);
            }else {
                // 当折叠次数不为1的时候，使用队列保存根结点
                Queue<Node> queue = new Queue<Node>();
                // 先将最顶端的根节点放入队列当中
                queue.enqueue(root);
                while (!queue.isEmpty()){
                    // 弹出第一个根节点
                    Node temNode = queue.dequeue();
                    // 如果根结点的左节点不为空，把左节点放入队列中
                    if (temNode.left!=null){
                        queue.enqueue(temNode.left);
                    }
                    // 如果根结点的右结点不为空，把右结点放入队列中
                    if(temNode.right!=null){
                        queue.enqueue(temNode.right);
                    }
                    // 如果根结点的左右结点都为空，则创建值为"down"的左节点，值为up的右结点
                    if(temNode.left==null&&temNode.right==null){
                        temNode.left = new Node(null,"down",null,null);
                        temNode.right = new Node(null,"up",null,null);
                    }
                }
            }
        }
        return root;
    }
}

测试结果

  public static void main(String[] args) {
        // 创建折叠三次的二叉树
        Node node = createFoldTree(3);
        // 打印二叉树
        printTree(node);
    }