数据结构和算法经典100题-第1题

说在开头的话：

如果拿金庸武侠做个比喻，数据结构和算法的学习就好比是程序员内功。内功的修炼往往不能一蹴而就，需要水滴石川。在博客中的这个分类中，专门记录我在数据结构和算法中的修炼。希望数据结构和算法的武林高手们多多指导，希望一起有志于提高内功的朋友们和我一起切磋进步。
从网络上看了很多关于数据结构和算法的学习方法。我采取的学习路线也并不是最好的，总结下来是：

• 观看麻省理工大学的公开课《算法导论》视频
• 阅读数据结构和算法的经典书籍《算法导论》
• 翻看书籍《大话数据结构》
• 阅读书籍《C++数据结构与算法》
  完成以上三个步骤后，主要还有两方面需要做
• 工作中做项目的设计中，选择合适和高效的数据结构
• 在休息的时候，做数据结构和算法经典100题

计划将数据结构和算法经典的100题用一个月的时间实现，博客中的数据结构和算法分类暂时会记录这方面的内容。

开始第一题：
输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。 要求不能创建任何新的结点，只调整指针的指向。
10
/ \
6 14
/ \ / \
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。

题目分析：
粗看此题目可以看到转换后的双向链表是按照从小到大的顺序排序的。而我们知道中序遍历一棵二元查找树就是按照值的从小到大的顺序访问树的各结点。那么我们这里就基本确定解此问题的方法的遍历方法为中序遍历。那么剩下的问题其实就是一个指针作为缓存暂存中间的结点信息。

程序源码：

/*
*
* 题目1
*输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。要求不能创建任何新的结点，只调整指针的指向。
*       10
*      / \
*     6   14
*    /\  /  \
*   4 8 12  16
*       
*   转换成双向链表  4=6=8=10=12=14=16。
* 
* 
*/

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>

using namespace std;

#define valueType int 
#define nodeNum 7

class node {
    public:
        node(int value);
        ~node();
        valueType m_value;
        node * m_left;
        node * m_right;
};

node::node(int value) {
    m_value = value;
    m_left = NULL;
    m_right = NULL;
}

node::~node() {

}

class bst_tree {
    public:
        bst_tree();
        ~bst_tree();
        node * get_root();
        void LDR(node* obj);
        void convert(node * obj);
    private:
        node * root;
};

bst_tree::bst_tree() {
    node *tmp_0 = new node(10);
    node *tmp_1 = new node(6);
    node *tmp_2 = new node(14);
    node *tmp_3 = new node(4);
    node *tmp_4 = new node(8);
    node *tmp_5 = new node(12);
    node *tmp_6 = new node(16);

    tmp_0->m_left = tmp_1;
    tmp_0->m_right = tmp_2;
    tmp_1->m_left = tmp_3;
    tmp_1->m_right = tmp_4;
    tmp_2->m_left = tmp_5;
    tmp_2->m_right = tmp_6;

    root = tmp_0;

}

/* Clipped... */
bst_tree::~bst_tree() {
    /* ... */
}

node* bst_tree::get_root() {
        return root;
}


/* Inorder traveral a bst Tree. */
void bst_tree::LDR(node * obj) {

//  cout<<"value:"<<obj->m_value<<endl;

    if (NULL != obj->m_left) {
        LDR(obj->m_left);
    }

//  cout<<"LDR:"<<obj->m_value<<endl;;
    convert(obj);

    if (NULL != obj->m_right) {
        LDR(obj->m_right);  
    }

    return;
}

node * g_double_list_head = NULL;
node * element_index = NULL;

/* Convert a bst-tree's node to a double-list node. */
void bst_tree::convert(node * obj) {

    if (NULL == element_index) {
        g_double_list_head = obj;
        element_index = obj;
        return;
    }

    obj->m_left = element_index;
    element_index->m_right = obj;

    //obj->m_right = NULL;
    element_index = obj;

    return;
}

int main(void) {

    /* Create a bst tree. */
    bst_tree * tree = new bst_tree();   
    tree->LDR(tree->get_root());        

    /* Traverse double-list. */
    node * tmp = g_double_list_head;
    while ( NULL != tmp ) {
        cout<<"Traverse double-list:"<<tmp->m_value<<endl;
        if (NULL != tmp->m_left) {
            cout<<"Traverse double-list m_left:"<<tmp->m_left->m_value<<endl;
        }

        if (NULL != tmp->m_right) {
            cout<<"Traverse double-list m_right:"<<tmp->m_right->m_value<<endl; 
        }

        tmp = tmp->m_right;
    }


    return 0;
}

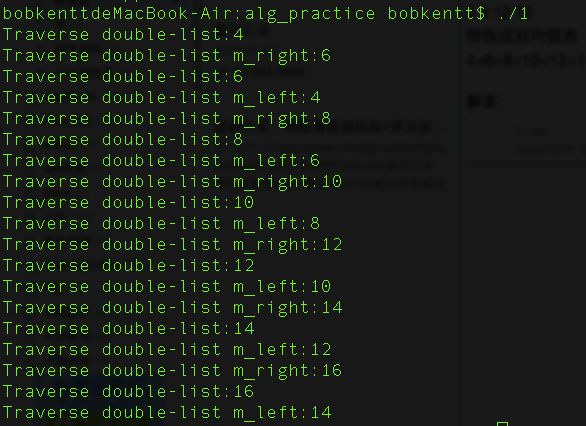
打印输出