回溯法-作业调度

问题定义

输入：

1.       任务数N

2.       机器数M

3.       随机序列长度t[i],其中t[i]=x表示第i个任务完成需要时间单位x，

输出：

1.       开销时间besttime，表示最佳调度需要时间单位

2.       最佳调度序列bestx[]，其中bestx[i]=x，表示将第i个任务分配给第x个机器执行。

实验思想

解空间的表示：

一个深度为N的M叉树。

基本思路：搜索从开始结点（根结点）出发，以DFS搜索整个解空间。

         每搜索完一条路径则记录下besttime 和bestx[]序列

开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处向纵深方向移至一个新结点，并成为一个新的活结点，也成为当前扩展结点。

如果在当前的扩展结点处不能再向纵深方向扩展，则当前扩展结点就成为死结点。

此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点；直至找到一个解或全部解。

        

测试数据及结果

本测试的硬件以及软件环境如下

         CPU：PM 1.5G; 内存:768M;操作系统：windows xp sp2;软件平台：JDK1.5;开发环境：eclipse

         如图1所示：即为求任务数为10机器数为5的最佳调度的算法结果。

图1

实验结论以及算法分析

通过测试证明算法正确有效。

性能分析的方法：使用JDK 1.5的System.nanoTime()，计算算法消耗的时间，以此来评价算法。（该方法在JDK1.5以下的版本中不支持）

为了不影响算法的准确度，在测试的过程我们注释掉了打印随机字符串的步骤。

由于没有使用限界函数进行优化，算法时间和空间复杂度呈指数级增长。所以该算法不适合较大规模的计算。

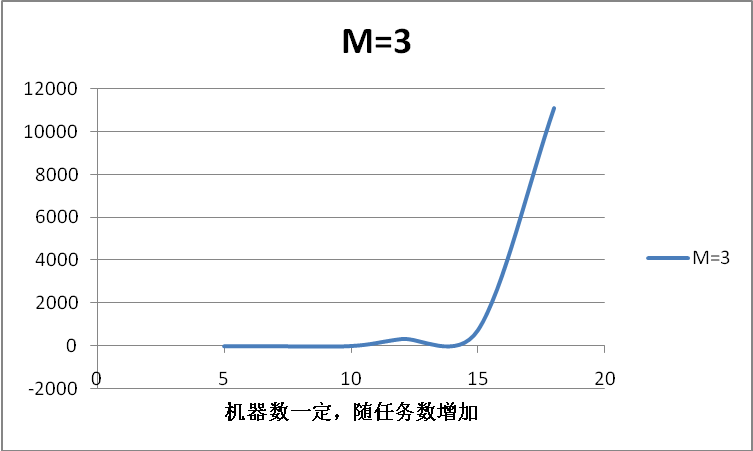
图2

图2 蓝线表示任务数一定M=3时，n增大时求解最佳调度对所消耗的时间，该趋势随着指数增加。

图3

图3表示任务数N一定时随着M的增大的增长曲线。

图2和图3表明该程序的时间复杂度与理论分析相符合。

源代码

最佳调度的回溯算法(java描述）

BestSchedule.Java

package  bestSchedule;

import  java.util.Random;

public   class  BestSchedule  {

    /**
     * @author icyfire
     * 本程序是采用回溯法解决最佳调度问题
     * 
     */
    int N;        //任务数
    int M;        //机器数
    int best;     //最优值
    int[] t;      //每个任务所需的时间序列
    int[] len;    //每台机器所需时间序列
    int[] x;      //当前路径
    int[] bestx;  //最优调度：其中bestx[i]=m表示把第i项任务分配给第m台机器
    
    
    
    public static void main(String[] args) {
     BestSchedule bs =new BestSchedule();
     bs.showTest();
    }
    
    void showTest()
    {
         N=10; // 任务数
         M=7; //机器数目
        Random r =new Random();
        t=new int [N]; //每个任务的时间
        //int sum=0;
        for (int i =0;i<N;i++)
        {
            t[i]=r.nextInt(5*N);
            //sum+=t[i];
        }
        len =new int [M];      //记录每台机器已经安排的时间
    
        best = Integer.MAX_VALUE;  
        bestx=new int [N];
        x =new int[N];
        
        Long startTime = System.nanoTime();
        backtrack(0);
        Long endTime = System.nanoTime();
        System.out.println("Totle time is " + (endTime - startTime) + " ns");
        
        System.out.println("best time:");
        System.out.println(best);
        System.out.println("each job costs:");
        for (int i=0;i<N;i++)
            System.out.print(t[i]+"  ");
        System.out.println(" best schedule:");
        for (int i=0;i<N;i++)
            System.out.print(bestx[i]+"  ");
        
            
        }
    //回溯搜索
    void backtrack (int dep)
    {
        
        if (dep==N)
        {
            
            int tmp = comp();
            if(tmp<best)
            {
                best=tmp;
                for(int i=0;i<N;i++)
                {
                    bestx[i]=x[i];
                }
            }
            return;
        }
    
        for(int i=0;i<M;i++)
        {
            len[i]+=t[dep];
            x[dep]=i+1;
            if(len[i]<best)
            {        
                backtrack(dep+1);    
            }
            
            len[i]-=t[dep];    
        }
    }
    
    //计算完成任务的时间
    int comp()
    {
        int tmp =0;
        for (int i=0;i<M;i++)
        {
            if(len[i]>tmp)
            {
                tmp=len[i];
            }
        }
        return tmp;
        
    }

}