用最简单的示例去理解Dijkstra最短路径算法[步骤分解]

铁松溜达py

已于 2024-05-11 00:34:36 修改

阅读量459

点赞数 4

文章标签：算法

于 2024-05-09 01:58:38 首次发布

本文链接：https://blog.csdn.net/book_dw5189/article/details/138591930

版权

Dijkstra算法是一种用于解决单源最短路径问题的经典算法，它能够计算出从单个源节点到图中所有其他节点的最短路径。

以下是Dijkstra算法的基本步骤：

初始化：将起始节点的距离设置为0，将所有其他节点的距离设置为无穷大（或一个较大的值）。将起始节点添加到优先级队列中。
迭代：重复以下步骤直到优先级队列为空：
- 从优先级队列中取出当前距离最短的节点。
- 遍历该节点的所有邻居节点，并更新它们的距离，如果通过当前节点到达邻居节点的路径比已知的最短路径更短，则更新邻居节点的距离，并将其添加到优先级队列中。
终止：当优先级队列为空时，算法结束，所有节点的最短路径已经计算完成。

Dijkstra算法的核心思想是通过不断地松弛边来逐步确定从起始节点到其他节点的最短路径。它保证了每个节点的距离值在算法执行过程中只会被更新一次，因此在没有负权边的情况下，可以得到正确的最短路径。

需要注意的是，Dijkstra算法仅适用于没有负权边的情况，如果图中存在负权边，需要使用其他算法，比如Bellman-Ford算法。

-----------
**Dijkstra算法**是一种用于查找从一个节点到图中所有其他节点的最短路径的算法。
它使用优先级队列来跟踪尚未处理的节点，并不断更新每个节点的最短路径。
**算法步骤：**
1. 初始化一个优先级队列，其中包含源节点和距离为0。
2. 初始化一个距离字典，其中包含所有节点和无穷大的距离。
3. 初始化一个前驱节点字典，其中包含所有节点和None值。
4. 只要优先级队列不为空，就执行以下步骤：
- 从优先级队列中弹出距离最小的节点。
- 遍历该节点的邻接节点，计算到每个邻接节点的距离。
- 如果找到更短的路径，就更新距离和前驱节点。
- 将邻接节点加入优先级队列。

--------------

# 在这个例子中，如果你从节点 1 出发，想找到到达节点 4 的最短路径，会使用 Dijkstra 算法。这意味着你会计算从一个节点到达另一个节点的最短距离。
# 这里是算法如何运作的简化过程：
# 1. 从节点 1 开始，距离初始值设为0，其他节点的距离设为无穷大。
# 2. 考虑从节点 1 出发，到节点 3 的距离是 5，到节点 2 的距离是 10。更新这两个节点的距离。
# 3. 从剩余节点中选择距离最短的一个。现在，节点 3 的距离最短，是5。所以选择节点 3，查看它的相邻节点。
# 4. 从节点 3 到节点 4 的距离是 1，加上先前的距离 5，等于6。所以更新节点 4 的距离为6。
# 5. 同样从节点 2 到节点 4 的距离是 1，加上节点 1 到节点 2 的距离是 10，总共是 11。但因为 6 比 11 小，所以不会重新更新节点 4，因为已经有了更短的路径。
# 所以，在这种情况下，程序会忽略从节点 2 经过的路径，因为已经有更短的路径（从节点 1 到 3 到 4）。

import heapq  # 导入用于实现优先级队列的模块
from colorama import init, Fore, Style

init()  # Initialize colorama

# 创建一个示例图
# 图的结构是一个字典，键是节点，值是邻接节点和对应的边权重
graph = {
    1: {2: 10, 3: 5},  # 节点1连接到节点2，权重是10；连接到节点3，权重是5
    2: {4: 1},         # 节点2连接到节点4，权重是1
    3: {4: 1},         # 节点3连接到节点4，权重是1
    4: {}   
}
  #     10
  # (1)---(2)
  #    |   |
  #  5 |   | 1
  #    |   |
  # (3)---(4)
  #     1

# Dijkstra算法函数
def dijkstra(graph, start):
    # 创建一个优先级队列
    pq = []  # 用来存储需要处理的节点
    # 初始化距离字典，所有节点的初始距离设为无穷大
    distances = {node: float('inf') for node in graph}
    distances[start] = 0  # 源节点的距离为0

    # 创建一个字典来存储每个节点的前驱节点，方便追踪路径
    previous = {node: None for node in graph}

    # 将源节点加入优先级队列
    heapq.heappush(pq, (0, start))  # (距离, 节点)
    a=1
    print('\n')



    # 处理优先级队列中的节点
    while pq:

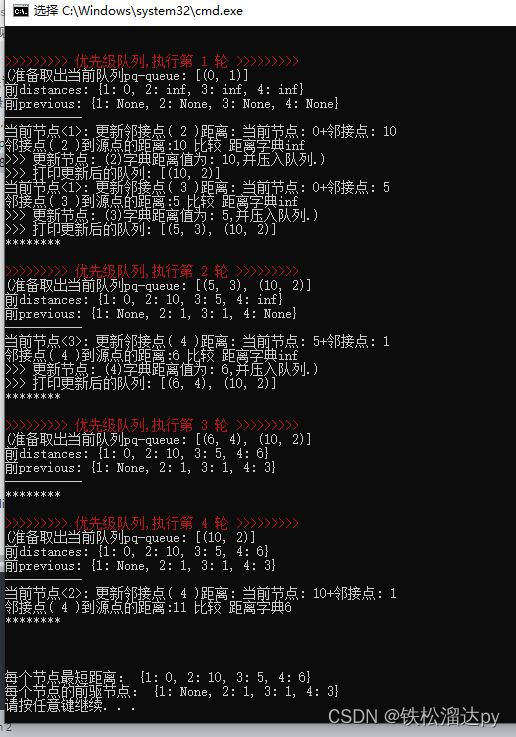
        print(Fore.RED + f'>>>>>>>>> 优先级队列,执行第 {a} 轮 >>>>>>>>>'+ Style.RESET_ALL)

        # 当 `pq = [(0, 1)]` 时，`current_distance` 和 `distances[current_node]` 分别是：
        # - `current_distance` 是从优先级队列中取出的当前节点的距离，current_distance= 0。
        # - `distances[current_node]` 是在 `distances` 字典中记录的当前节点的已知最短距离。对于源节点，即节点 1，它的已知最短距离也是 0。
        # 所以在这种情况下，`current_distance` 和 `distances[current_node]` 都是 0。 

        print('(准备取出当前队列pq-queue:',pq)
        print('前distances:',distances)
        print('前previous:',previous)
        print('-----------')
        # 从优先级队列中取出距离最短的节点
        current_distance, current_node = heapq.heappop(pq)

        # 如果当前距离大于已知的最短距离，则继续
        # 如果发现从当前节点出发的路径到达的某个节点的距离大于已知的距离，则说明已经找到了一条更短的路径，因此可以跳过该节
        if current_distance > distances[current_node]:
            continue  # 这条路径不再有效，跳过; continue语句的作用是重新开始循环，跳过当前循环中的剩余代码，直接进入下一次循环。

        # 遍历当前节点的邻接节点
        for neighbor, weight in graph[current_node].items():
            # 计算从当前节点到邻接节点的距离
            distance = current_distance + weight

            print(f'当前节点<{ current_node }>: 计算邻接点( {neighbor} )距离: 当前节点: {current_distance}+邻接点: {weight}')
            print(f"邻接点( {neighbor} )到源点的距离:{distance} 比较 距离字典{distances[neighbor]}")


            # 如果发现更短的路径，则更新
            if distance < distances[neighbor]:
                distances[neighbor] = distance  # 更新距离
                previous[neighbor] = current_node  # 更新前驱节点
                print(f'>>> 更新节点: ({neighbor})字典距离值为: {distances[neighbor]},并压入队列.)')
                # 将邻接节点加入优先级队列
                heapq.heappush(pq, (distance, neighbor))
                print(f'>>> 打印更新后的队列: {pq}')
        print('********\n')        
        a=a+1
    return distances, previous  # 返回最终的距离和前驱节点信息

# 从节点1开始运行Dijkstra算法
distances, previous = dijkstra(graph, 1)

print("\n\n每个节点最短距离：", distances)  # 打印每个节点的最短距离
print("每个节点的前驱节点：", previous)   # 打印每个节点的前驱节点

# 在这个例子中，如果你从节点 1 出发，想找到到达节点 4 的最短路径，你会使用 Dijkstra 算法。这意味着你会计算从一个节点到达另一个节点的最短距离。
# 这里是算法如何运作的简化过程：
# 1. 从节点 1 开始，距离初始值设为0，其他节点的距离设为无穷大。
# 2. 考虑从节点 1 出发，到节点 3 的距离是 5，到节点 2 的距离是 10。更新这两个节点的距离。
# 3. 从剩余节点中选择距离最短的一个。现在，节点 3 的距离最短，是5。所以选择节点 3，查看它的相邻节点。
# 4. 从节点 3 到节点 4 的距离是 1，加上先前的距离 5，等于6。所以更新节点 4 的距离为6。
# 5. 同样从节点 2 到节点 4 的距离是 1，加上节点 1 到节点 2 的距离是 10，总共是 11。但因为 6 比 11 小，所以不会重新更新节点 4，因为已经有了更短的路径。
# 所以，在这种情况下，程序会忽略从节点 2 经过的路径，因为已经有更短的路径（从节点 1 到 3 到 4）。

# 在Dijkstra算法中，确保每个节点只被访问一次并且在找到更短路径后不会再次考虑该节点的部分通常通过以下方式实现：
# 1. **优先级队列（Priority Queue）的使用**：Dijkstra算法通常使用优先级队列来管理要探索的节点。
# 在每次迭代中，从优先级队列中选择当前距离最短的节点进行处理。这确保了每个节点只被访问一次。
# 2. **距离字典的更新**：在发现更短路径后，会更新距离字典中该节点的距离值。
# 这意味着即使后续有其他路径经过该节点，由于已经发现了更短的路径，因此不会再考虑该节点。
# 3. **跳过已处理节点**：如果在优先级队列中发现某个节点的当前距离已经大于已知的最短距离，则跳过对该节点的处理。
# 这确保了在找到更短路径后不会重复考虑该节点。
# 这些机制确保了Dijkstra算法在搜索过程中每个节点只被访问一次，并且在找到更短路径后不会再次考虑该节点，从而提高了算法的效率和性能。

# Dijkstra算法确保在搜索过程中每个节点只被访问一次。这是因为在算法执行过程中，每个节点被标记为已访问，并且仅在第一次访问时才会被添加到最短路径集合中。

# 具体来说，Dijkstra算法使用一个优先级队列（通常是最小堆）来选择下一个要访问的节点。
# 每次从优先级队列中选择距离最短的节点进行处理，然后将其标记为已访问。
# 在处理节点时，算法会检查与当前节点相邻的节点，并根据当前节点到相邻节点的路径长度更新相邻节点的最短距离。
# 然后，将这些相邻节点添加到优先级队列中以供后续处理。

# 由于优先级队列的特性，每个节点只会被处理一次：当节点被处理时，它被标记为已访问，并且以后不会再次被处理。
# 这确保了在算法的整个执行过程中，每个节点只被访问一次，从而保证了算法的正确性和效率。

# **Dijkstra算法**是一种用于查找从一个节点到图中所有其他节点的最短路径的算法。
# 它使用优先级队列来跟踪尚未处理的节点，并不断更新每个节点的最短路径。
# **算法步骤：**
# 1. 初始化一个优先级队列，其中包含源节点和距离为0。
# 2. 初始化一个距离字典，其中包含所有节点和无穷大的距离。
# 3. 初始化一个前驱节点字典，其中包含所有节点和None值。
# 4. 只要优先级队列不为空，就执行以下步骤：
#     - 从优先级队列中弹出距离最小的节点。
#     - 遍历该节点的邻接节点，计算到每个邻接节点的距离。
#     - 如果找到更短的路径，就更新距离和前驱节点。
#     - 将邻接节点加入优先级队列。
# 5. 返回距离和前驱节点字典。
'''


当我们遍历图并更新节点的距离时，我们会检查当前距离（从源节点到当前节点的距离）是否小于字典中存储的距离（从源节点到当前节点的当前已知最短距离）。
如果当前距离更短，则我们更新字典中的距离，因为我们找到了从源节点到当前节点的一条更短的路径。
### 具体步骤如下：
1. 从优先级队列中取出距离最小的节点 `current_node`。
2. 遍历 `current_node` 的邻接节点 `neighbor` 和对应的边权重 `weight`。
3. 计算从 `current_node` 到 `neighbor` 的距离 `distance`。
4. 如果 `distance` 小于当前存储在字典 `distances` 中的 `neighbor` 的距离，则更新 `distances[neighbor]` 为 `distance`。
5. 将 `neighbor` 添加到优先级队列中，如果它不在队列中。
### 示例：
假设我们有一个图如下：
```
  #     10
  # (1)---(2)
  #    |   |
  #  5 |   | 1
  #    |   |
  # (3)---(4)
  #     1
```
我们从节点 1 开始运行 Dijkstra 算法。
**第一步：**
* 取出距离最小的节点，即节点 1。
* 遍历节点 1 的邻接节点，即节点 2 和节点 3。
**第二步：**
* 计算从节点 1 到节点 2 的距离：`distance = 10`。
* 检查字典 `distances` 中存储的节点 2 的距离：`distances[2] = inf`。
* 由于 `distance` 小于 `distances[2]`，因此更新 `distances[2]` 为 `10`。
**第三步：**
* 计算从节点 1 到节点 3 的距离：`distance = 5`。
* 检查字典 `distances` 中存储的节点 3 的距离：`distances[3] = inf`。
* 由于 `distance` 小于 `distances[3]`，因此更新 `distances[3]` 为 `5`。
经过这两步，字典 `distances` 更新如下：
```
{1: 0, 2: 10, 3: 5, 4: inf}
```
我们继续遍历图，更新其他节点的距离，直到找到从源节点到所有其他节点的最短路径。
我希望这个解释能帮助你理解 Dijkstra 算法中更新节点距离的过程。
'''

----------

在 Dijkstra 算法中，除了更新节点的距离外，我们还需要同时更新优先级队列和前驱。
**更新节点的距离：**
当我们遍历图并更新节点的距离时，我们会检查当前距离（从源节点到当前节点的距离）是否小于字典中存储的距离（从源节点到当前节点的当前已知最短距离）。
如果当前距离更短，则我们更新字典中的距离，因为我们找到了从源节点到当前节点的一条更短的路径。
**更新优先级队列：**
当我们更新某个节点的距离时，我们需要检查该节点是否已经在优先级队列中。如果在，则需要更新其优先级（距离）。如果不在，则需要将该节点添加到优先级队列中。
**更新前驱：**
当我们更新某个节点的距离时，还需要更新其前驱。前驱是指从源节点到该节点的最短路径上的前一个节点。

# 在Dijkstra算法中，确保每个节点只被访问一次并且在找到更短路径后不会再次考虑该节点的部分通常通过以下方式实现：
# 1. **优先级队列（Priority Queue）的使用**：Dijkstra算法通常使用优先级队列来管理要探索的节点。
# 在每次迭代中，从优先级队列中选择当前距离最短的节点进行处理。这确保了每个节点只被访问一次。
# 2. **距离字典的更新**：在发现更短路径后，会更新距离字典中该节点的距离值。
# 这意味着即使后续有其他路径经过该节点，由于已经发现了更短的路径，因此不会再考虑该节点。
# 3. **跳过已处理节点**：如果在优先级队列中发现某个节点的当前距离已经大于已知的最短距离，则跳过对该节点的处理。
# 这确保了在找到更短路径后不会重复考虑该节点。
# 这些机制确保了Dijkstra算法在搜索过程中每个节点只被访问一次，并且在找到更短路径后不会再次考虑该节点，从而提高了算法的效率和性能。