因为PCA内要求特征矩阵的协方差矩阵,貌似学的数学已经交给老师了,补一下:
协方差矩阵的每个元素是各个矢量元素之间的协方差。这是从标量随机变量到高维度随机矢量的自然推广。
假设X是以n个标量随机变量组成的行矢量,
并且μi是其第i个元素的期望值,即, μi = E(Xi)。协方差矩阵被定义的第i,j项是如下:
即:
矩阵中的第(i,j)个元素是Xi与Xj的协方差。这个概念是对于标量随机变量方差的一般化推广。
作用:它能导出一个变换矩阵(也就是协方差矩阵),这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。
根据这个协方差矩阵A,计算特征值和特征向量。
但我的问题是如何这个 特征方程怎么写呢? AX=aX;
求得所有使方程成立的a,这里的a就是所谓的本征向量;同时取得特征值;
然后把本征向量从大到小排序;
选择前m个构成投影矩阵L;
然后把源矩阵*现在的投影矩阵L = 降维后的矩阵,也就是最后PCA的结果啦!
个人学习总结,错的话请指出!哈哈









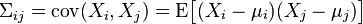
![\Sigma=\mathrm{E}\left[ \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right) \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right)^\top\right]](http://upload.wikimedia.org/wikipedia/zh/math/d/4/b/d4b4b5ba16ff9e84f3e84e48993afdde.png)
![=\begin{bmatrix} \mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\ \mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]\end{bmatrix}](http://upload.wikimedia.org/wikipedia/zh/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)














 3140
3140

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








