如何理解协方差矩阵（散布矩阵）

这学期开了模式识别的学习课程，经常提到概率论与数理统计的一个概念：协方差矩阵（在模式识别中又叫散布矩阵）。理解这个矩阵严格意义上来说其实不需要太多先导知识，我们只需要了解一些线性代数基本的概念。但是你如果不了解协方差矩阵，听模式识别的课程就会云里雾里（就像我一样）。

那么在学习协方差矩阵之前

首先你需要知道一些统计学的基本概念

1.均值：

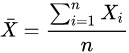
2.样本标准差：

均值很好理解，是描述样本集合中的中间点，是所有信息的平均。而标准差描述的是一种散布度，比如[0,10,11]和[6,7,8]的均值是一样的都是7，但是很明显[0,10,11]看起来会更加分散一点，这就是散布程度更大一点。

这里从我的角度提一嘴为什么样本标准差中的分母是 $x-1$ 。我们知道 $\bar{x}$是样本中的均值，均值反映的信息和样本整体有关，也就是和样本中的每个值都有关系，因此其实我们可以把均值理解为包含样本中n种信息，而 $x_i$这个值本身表示样本中的一个信息（这个应该很好理解），那么 $x_i-\bar{x}$就可以理解为包含 $n-1$ 种信息，那么对于方差来说，这就达到了估计的目的，这也被称为样本的无偏估计。而如果分母为 $n$ 的话，很明显就变成了样本的有偏估计。

这个理解方式的启发其实是机器学习中的卷积层，卷积层这一层的作用就是将图像信息压缩：图像经过卷积以后，虽然经过降维，但是图像包含的信息仍然是原有经过降维处理后信息。

下面对于协方差的理解引用了部分其他博主的理解，我觉得理解起来相对会轻松一点

协方差可以说是在标准差的基础上延申出来的，我们面对多维数据，无法用一个固定的值描述样本的离散程度，协方差就是度量两个随机变量关系的统计量。

首先我们看方差的定义：

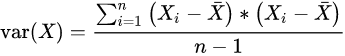
这是度量单维度偏离均值程度的式子，接着就是协方差：

可以看出来，协方差矩阵可以写成对于每一维来说的方差，只不过是以矩阵形式写出来的方差，举一个三维的最简单的例子

从这个例子可以看出来，首先 $\mathrm{cov}(x)$ 代表在 $x$ 变量中的方差，可以看作是$\mathrm{var}(X)=\frac{{\sum }_{i=1}^n\left(X_i-\bar{X}\right)\ast \left(X_i-\bar{X}\right)}{n-1}$单独的样本方差，而更重要的是 $\mathrm{cov}(x,y)$ 表示$\mathrm{cov}(X,Y)=\frac{{\sum }_{i=1}^n\left(X_i-\bar{X}\right)\ast \left(Y_i-\bar{Y}\right)}{n-1}$，这样以此类推。从这种定义角度可以发现，这就是多维变量之间的完全图关系，而这种关系从某种意义上来说就是他们的互相之间的离散程度，但更准确的说是相关系数。如果这种结果为正值就说明他们是正相关的，结果为负值说明他们之间是负相关的。

在这里，也给出协方差矩阵的计算方式：先让样本矩阵中心化，即每一维度减去该维度的均值得到矩阵 $X$ ，使每一维度上的均值为0，直接用矩阵 $X$ 乘上它的转置 $X^T$ ，然后除以 $n-1$ 即可。