高中数学：指数、对数、幂函数综合（拔高）

一、需要掌握的重要函数

1、第一组（记住）

例题
1、判断奇偶性
2、代值定象限

2、第二组（记住）

以下几个函数都是奇函数

3、常用知识点

1、找对称中心或对称轴

上加下减，左加右减

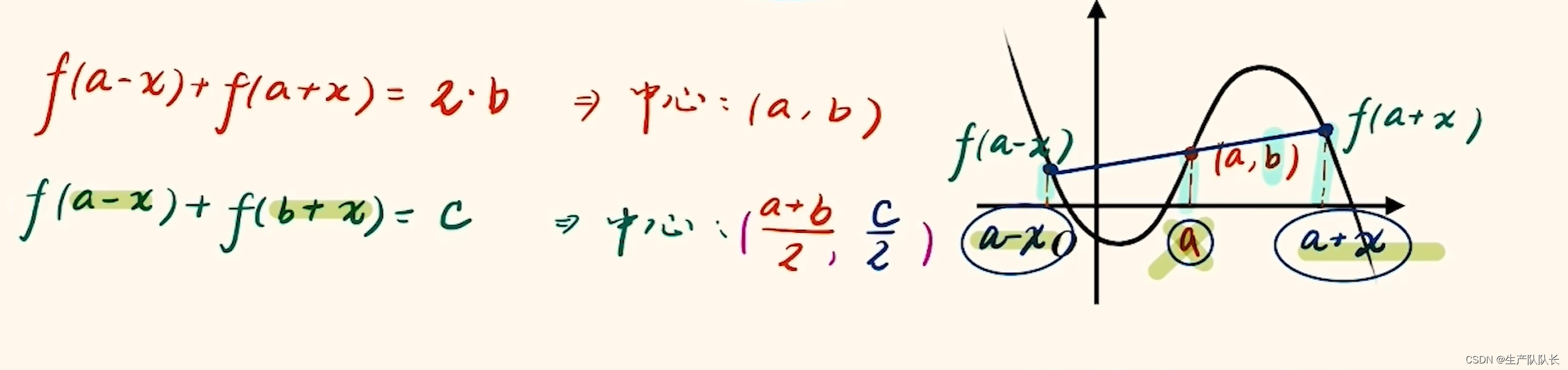
2、奇偶函数组合后的奇偶性

3、NB公式（处理中心对称图像的求和问题）

4、函数不等式解法

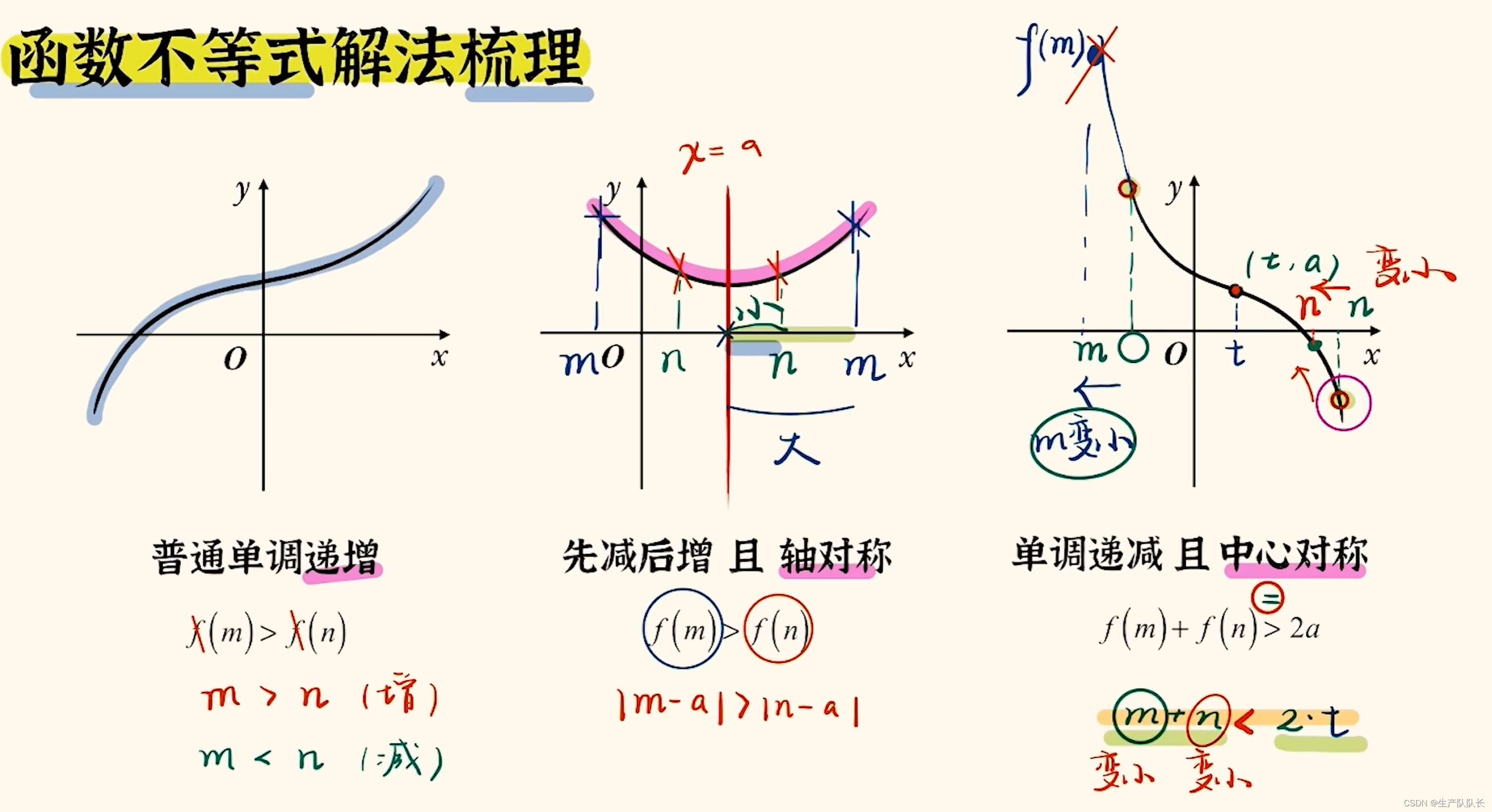
5、最值判断

二、题型汇总

1、求和问题

一般解题思路：

1、判断奇偶性
2、找对称中心或对称轴
3、必要时候，需要对函数式换元变形
4、NB公式
换元后，需要重新计算定义区间
注：在定义区间D上，如果该函数有对称中心或者有对称轴，那么，一定可以通过换元，将函数变成>奇函数或者偶函数。

例题1

一对关于对称中心对称的点求和

例题2

N对关于对称中心对称的点求和

2、解不等式

一般解题思路：

1、对称性：找对称中心或对称轴
2、单调性（用于去f）
3、解不等式

例题1

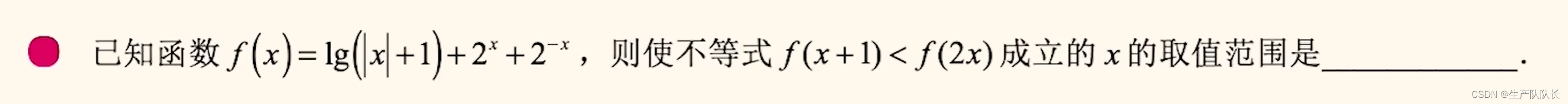
例题2

3、恒成立求参数

一般解题思路：
所有恒成立问题，都可以转化为最值问题（分离参数法）
函数式变形（平方差公式、换元法等）
确定变形后的函数式定义域

例题

三、总结

1、如果是f外含参数不等式，则把自变量代入f(x)，得出新的不等式
利用分离参数法，得出一个新的函数式，求解该函数的最值即可。

2、如果f外不含参数，则
直接计算
f(x)+f(-x)或f(x)-f(-x)
找出对称中心或者对称轴